2-3第二章概率复习 课件(23张PPT)
文档属性
| 名称 | 2-3第二章概率复习 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 206.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 09:21:33 | ||
图片预览








文档简介
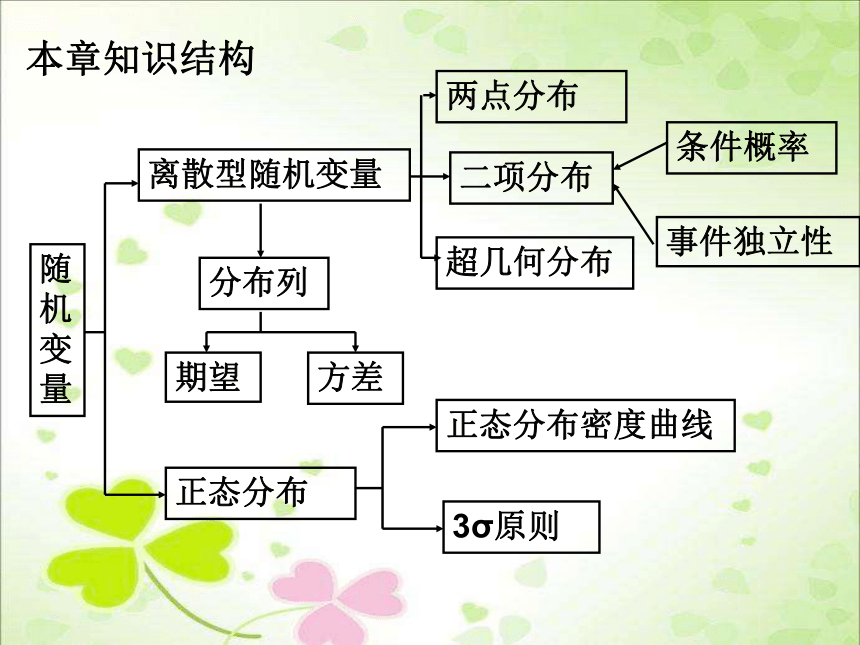
课件23张PPT。第二章 概率复习本章知识结构随机变量离散型随机变量分布列期望方差正态分布两点分布二项分布超几何分布正态分布密度曲线3σ原则条件概率事件独立性随着实验的结果变化而变化的变量叫做随机变量。1.随机变量的概念:随机变量所有可能取的值都能一一列出(可以是无限个)这样的随机变量叫做离散型随机变量.2.离散型随机变量知识点回顾称为随机变量X的概率分布,简称X的分布列.3.定义:概率分布(分布列)4.离散型随机变量的分布列具有下述两个性质:5.求离散型随机变量的概率分布列的步骤:(1)找出随机变量X的所有可能的取值(2)求出各取值的概率(3)列成表格P(X=xi)=pi则称表5.条件概率的定义:求条件概率的常用方法:
(2)借助古典概型公式P(B|A)=(1)定义:即P(B|A)=在已知事件A发生的条件下,事件B发生的概
率叫做条件概率,记为P(B|A)6.两个事件相互独立的定义:事件A是否发生对事件B的发生的概率没有影响,则称事件A与事件B相互独立.如果AB为两个相互独立事件,则P(AB)=P(A)P(B),结论7、什么叫n次独立重复试验?8、什么叫二项分布?定义:在相同条件下重复做的n次试验且各试验的结果相互独立,称它们为n次独立重复试验。在n次独立重复试验中事件A恰好发生k次的概率是并称p为成功概率定义:在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么 9、 超几何分布:设总数为N件的两类物品其中一类为M件,从所有物品中任取n件(n≤N)这n件中所含这类物品件数X是一个随机变量它取值k的概率P(X=k)= , k=0,1,2,…,m,则称随机变量X分布列
为 .也称X服从参数为N,M,n超几何分布.超几何分布列10、离散型随机变量取值的平均值数学期望11、数学期望的性质期望反映了离散型随机变量取值的平均水平.12、如果随机变量X服从二 点分布,则13、如果随机变量X服从二项分布,即X~B(n,p),则14、如果随机变量X服从超几何分布,
则pnp15.离散型随机变量取值的方差一般地,若离散型随机变量X的概率分布为:则随机变量X的方差为称为随机变量X的标准差。它是反映离散程度的量,它的值越小,则随机变量越集中于均值。16.几个常用公式: 17正态曲线的性质1.设随机变量X的分布列p(X=k)= (k=1,2,3,4,5,6)3.设8件产品中有3件次品,从中任取2件产品。已知在所取的产品中有1件是次品的条件下,求另一件也是次品的概率.则P(1.521 1
64.(湖南)设随机变量X服从正态分布N(2,9), 若P(X>c+1)=P(XA.1 B.2 C.3 D.45.已知在6个电子元件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将2个次品全部找出的概率( )
A.1/5 B.4/15 C. 2/5 D.14/15BB6、(2009全国卷2)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。(1)求从甲、乙两组各抽取的人数;(2)求从甲组抽取的工人中恰有1名女工人的概率;(3)记X表示抽取的3名工人中男工人数,求X的分布列及数学期望。2)超几何分布、二项分布与期望和方差7.(09北京)某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min.(1)求这名学生在上学路上到第三个路口时首次
遇到红灯的概率;(2)求这名学生在上学路上因遇到红灯停留的总时间X的分布列(Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A,因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为(Ⅱ)由题意可得,X可能取的值为0,2,4,6,8(单位:min).事件X=2k等价于事件“该学生在路上遇到k次红灯(k=1,2,3,4)∴
∴即X的分布列是∴X的期望是8.在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:(1) 取出的3件产品中一等品件数X的分布列和数学期望(2) 取出的3件产品中一等品件数多于二等品件数的概率。4)点击高考解(1):题由意可知随机变量X服从超几何分布从10件产品中任取3件恰有k件一等品的概率为P(X=k)= k=0,1,2,3所以随机变量X的分布列为所以X的数学期望E(X)=0× +1× +2× + 3× =(2)P=9.有同寝室的四位同学分别写一张贺年卡,先集中起来,然后每人去拿一张。记自己拿到自己写的贺年卡的人数为X. 求随机变量X的分布列,并求E(X)解:由题意可得:X所有可能值为4张贺卡4人来取总的取法有4人都没取到自己的贺卡共有3×3×1×1=9种方法∴P(X=0)= =同理P(X=1)= P(X=2)= P(X=4)=∴所以X的分布列为∴E(X)=0× + 1× + 2× +4× =10,1,2,44×3×2×1=24种6)作业布置
2-3第二章概率综合复习测试试卷5)归纳小结1、熟练应用排列组合与计数原理的求概率2、超几何分布与二项分布的区分和应用3、认真审题的好习惯做到不重复不遗漏
(2)借助古典概型公式P(B|A)=(1)定义:即P(B|A)=在已知事件A发生的条件下,事件B发生的概
率叫做条件概率,记为P(B|A)6.两个事件相互独立的定义:事件A是否发生对事件B的发生的概率没有影响,则称事件A与事件B相互独立.如果AB为两个相互独立事件,则P(AB)=P(A)P(B),结论7、什么叫n次独立重复试验?8、什么叫二项分布?定义:在相同条件下重复做的n次试验且各试验的结果相互独立,称它们为n次独立重复试验。在n次独立重复试验中事件A恰好发生k次的概率是并称p为成功概率定义:在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么 9、 超几何分布:设总数为N件的两类物品其中一类为M件,从所有物品中任取n件(n≤N)这n件中所含这类物品件数X是一个随机变量它取值k的概率P(X=k)= , k=0,1,2,…,m,则称随机变量X分布列
为 .也称X服从参数为N,M,n超几何分布.超几何分布列10、离散型随机变量取值的平均值数学期望11、数学期望的性质期望反映了离散型随机变量取值的平均水平.12、如果随机变量X服从二 点分布,则13、如果随机变量X服从二项分布,即X~B(n,p),则14、如果随机变量X服从超几何分布,
则pnp15.离散型随机变量取值的方差一般地,若离散型随机变量X的概率分布为:则随机变量X的方差为称为随机变量X的标准差。它是反映离散程度的量,它的值越小,则随机变量越集中于均值。16.几个常用公式: 17正态曲线的性质1.设随机变量X的分布列p(X=k)= (k=1,2,3,4,5,6)3.设8件产品中有3件次品,从中任取2件产品。已知在所取的产品中有1件是次品的条件下,求另一件也是次品的概率.则P(1.5
64.(湖南)设随机变量X服从正态分布N(2,9), 若P(X>c+1)=P(X
A.1/5 B.4/15 C. 2/5 D.14/15BB6、(2009全国卷2)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。(1)求从甲、乙两组各抽取的人数;(2)求从甲组抽取的工人中恰有1名女工人的概率;(3)记X表示抽取的3名工人中男工人数,求X的分布列及数学期望。2)超几何分布、二项分布与期望和方差7.(09北京)某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min.(1)求这名学生在上学路上到第三个路口时首次
遇到红灯的概率;(2)求这名学生在上学路上因遇到红灯停留的总时间X的分布列(Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A,因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为(Ⅱ)由题意可得,X可能取的值为0,2,4,6,8(单位:min).事件X=2k等价于事件“该学生在路上遇到k次红灯(k=1,2,3,4)∴
∴即X的分布列是∴X的期望是8.在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:(1) 取出的3件产品中一等品件数X的分布列和数学期望(2) 取出的3件产品中一等品件数多于二等品件数的概率。4)点击高考解(1):题由意可知随机变量X服从超几何分布从10件产品中任取3件恰有k件一等品的概率为P(X=k)= k=0,1,2,3所以随机变量X的分布列为所以X的数学期望E(X)=0× +1× +2× + 3× =(2)P=9.有同寝室的四位同学分别写一张贺年卡,先集中起来,然后每人去拿一张。记自己拿到自己写的贺年卡的人数为X. 求随机变量X的分布列,并求E(X)解:由题意可得:X所有可能值为4张贺卡4人来取总的取法有4人都没取到自己的贺卡共有3×3×1×1=9种方法∴P(X=0)= =同理P(X=1)= P(X=2)= P(X=4)=∴所以X的分布列为∴E(X)=0× + 1× + 2× +4× =10,1,2,44×3×2×1=24种6)作业布置
2-3第二章概率综合复习测试试卷5)归纳小结1、熟练应用排列组合与计数原理的求概率2、超几何分布与二项分布的区分和应用3、认真审题的好习惯做到不重复不遗漏
