1.3.2 杨辉三角 课件32张PPT
文档属性
| 名称 | 1.3.2 杨辉三角 课件32张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览






文档简介
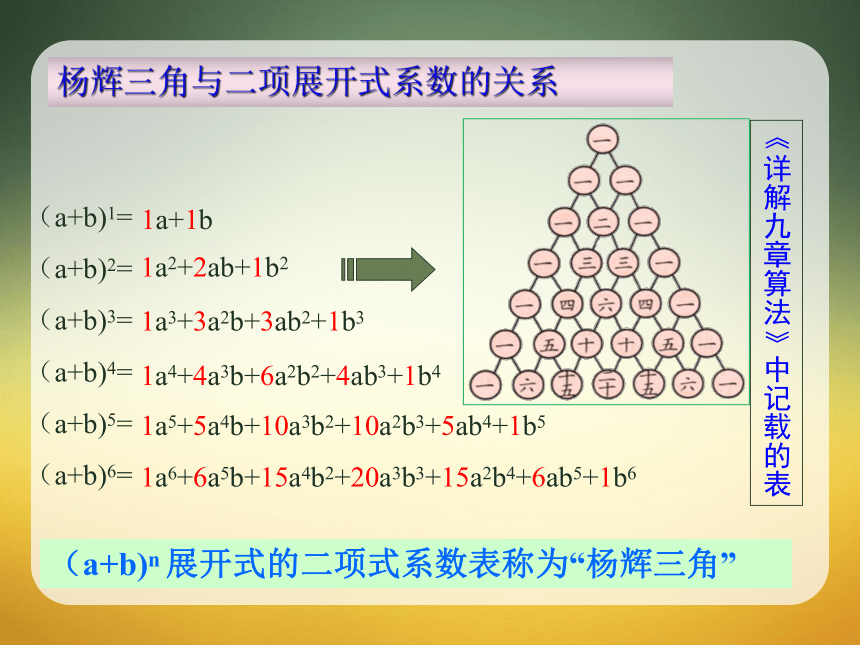
课件32张PPT。1.3.2杨辉三角高中数学人教B版选修2-31.二项式定理:(a+b)n=Cn0an+Cn1an-1b1+…+Cnran-rbr+…+Cnnbn2.通项:Tr+1=Cnran-rbr复习:3.二项式系数:课前预习:“杨辉三角”?(a+b)1=
(a+b)2=
(a+b)3=
(a+b)4=
(a+b)5=
(a+b)6=
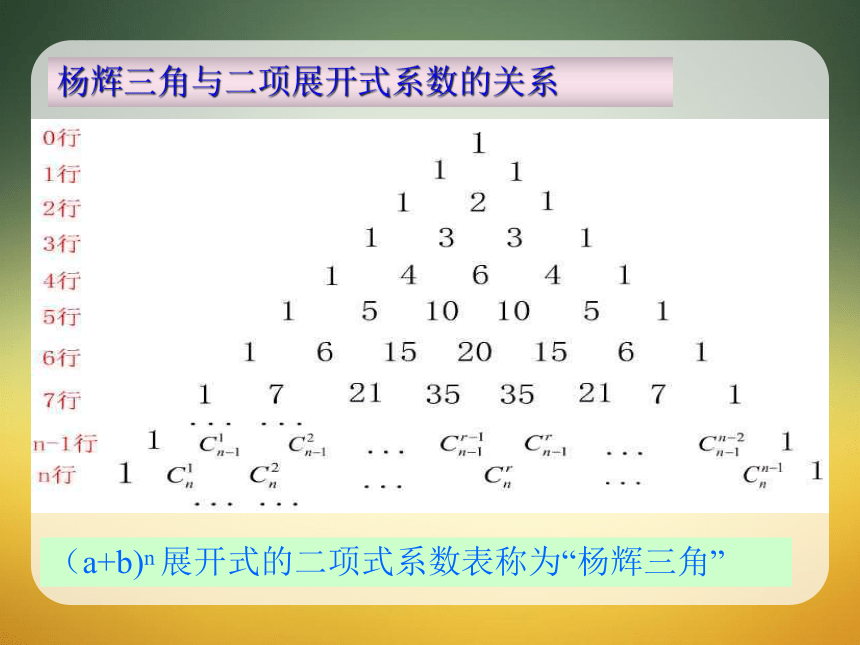
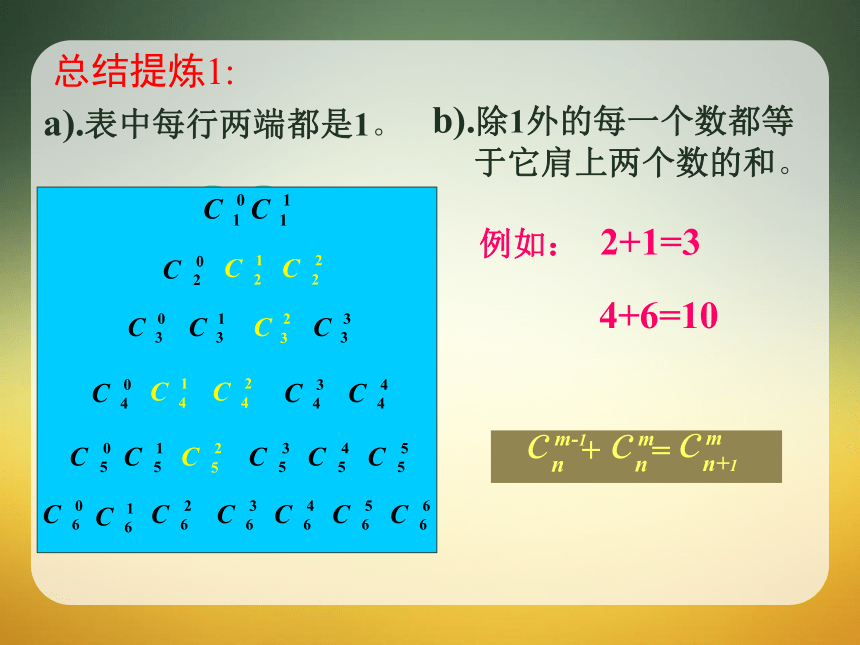
1a+1b1a2+2ab+1b21a3+3a2b+3ab2+1b31a4+4a3b+6a2b2+4ab3+1b41a5+5a4b+10a3b2+10a2b3+5ab4+1b51a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6杨辉三角与二项展开式系数的关系(a+b)n 展开式的二项式系数表称为“杨辉三角”《详解九章算法》中记载的表杨辉三角与二项展开式系数的关系(a+b)n 展开式的二项式系数表称为“杨辉三角”1解决问题:如图,在由二项式系数所构成的杨辉三角形中,第 _____行中从左至右第14与第15个数的比为2:3.1.3.2杨辉三角议一议1)请看系数有没有明显的规律?2)上下两行有什么关系吗? 一、二项式系数性质:a).表中每行两端都是1。b).除1外的每一个数都等
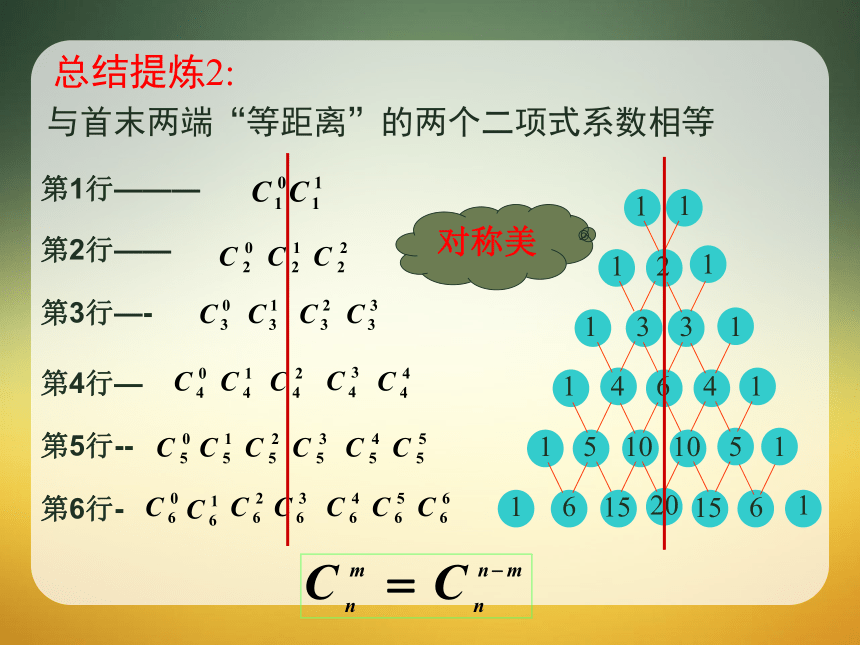
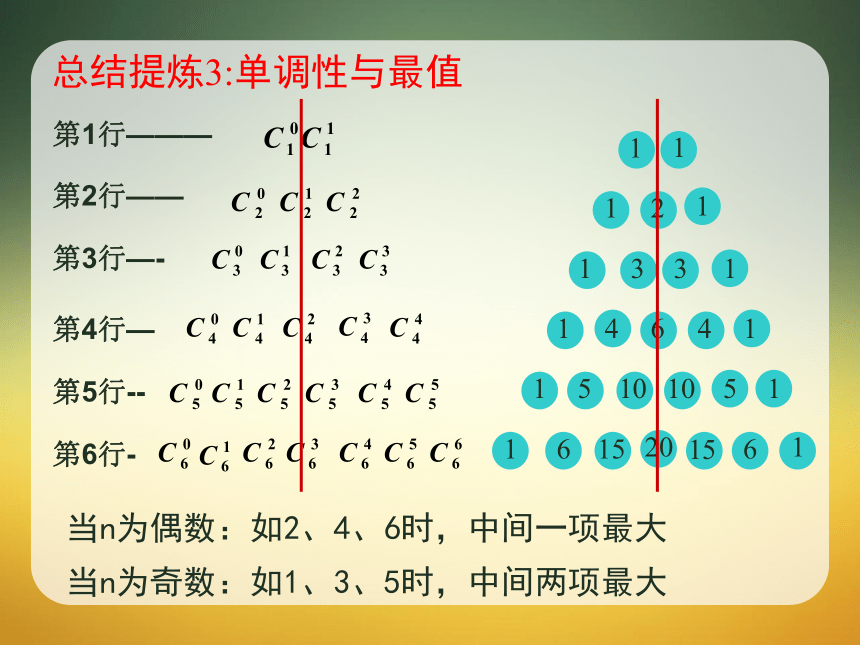
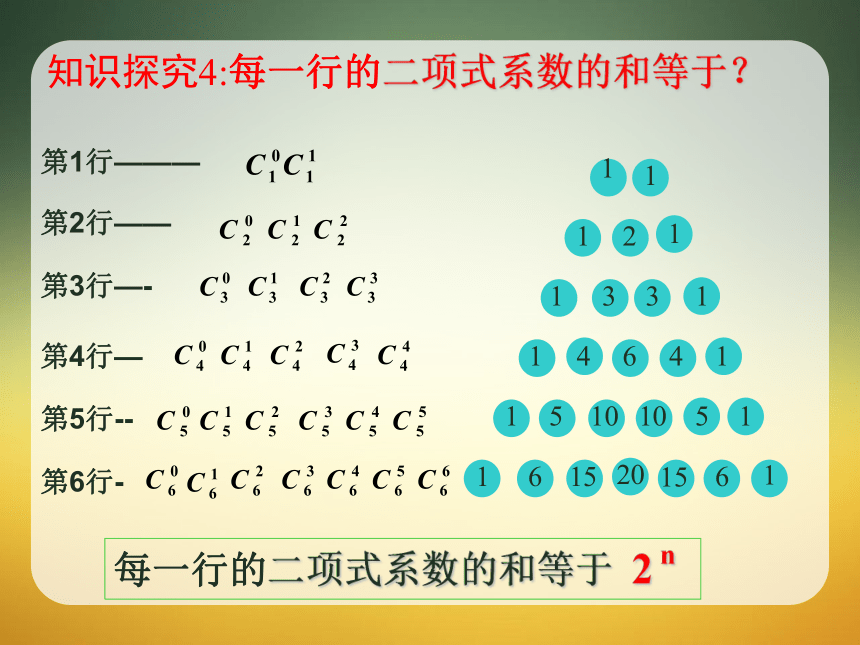
于它肩上两个数的和。4+6=10总结提炼1:对称美总结提炼2: 与首末两端“等距离”的两个二项式系数相等当n为偶数:如2、4、6时,中间一项最大当n为奇数:如1、3、5时,中间两项最大总结提炼3:单调性与最值知识探究4:每一行的二项式系数的和等于?每一行的二项式系数的和等于 2 n 学以致用:方法赋值法学以致用:变式2:方法:求奇次项系数之和与偶次项系数的和
可以先赋值,然后解方程组整体求解赋值法二、杨辉三角的进一步探索1.杨辉三角的第2k-1行的各数字特点 第2k-1行(k是正整数)的各个数字都是奇数。第1行第6行第2行第3行第4行第5行第7行第0行12.第1行第6行第2行第3行第4行第5行第7行第0行所有行的第二个数构成等差数列3.第1行第6行第2行第3行第4行第5行第7行第0行所有行的第三个数都是三角形数4.古希腊数学家:1,3,6,10,15,21…这些数量的(石子),都可以排成三角形第1行第6行第2行第3行第4行第5行第7行第0行n行中的第i个数是斜行i-1中前n-1个数之和 第1行第6行第2行第3行第4行第5行第7行5.第0行三、欣赏有趣的杨辉三角 1,1,2,3,5,8,13,21,34,... 1.斐波那契“兔子繁殖问题”此数列{an}满足, a1=1,a2=1, 且an=an-1+an-2 (n≥3)
这就是著名的斐波那契数列. 中世纪意大利数学家斐波那契的传世之作《算术之法》中提出了一个饶有趣味的问题:假定一对刚出生的兔子一个月就能长成大兔子,再过一个月就开始生下一对小兔子,并且以后每个月都生一对小兔子.设所生一对兔子均为一雄一雌,且均无死亡.问一对刚出生的小兔一年内可以繁殖成多少对兔子? 从杨辉三角得到答案:1,1,2,3,5,8,13,21,34,... 13
8
5
3
2
1
1大自然中的斐波那契数列----树丫的数目大自然中的斐波那契数列---种子的排列(松果)1弹球游戏,小球向容器内跌落,碰到第一层阻挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落碰到第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品(AG区奖品最好,BF区奖品次之,CE区奖品第三,D 区奖品最差)。 A B C D E F G2. 弹球游戏1 华罗庚是这样解释:钢珠从每一通道通过的可能情况是:任何一层的左右两边的通道都只有一个可能情形,而其他任一个通道的可能情形,等于它左右肩上两个通道的可能情形相加。于是,钢珠通过每一层每个通道的可能情形是:第五层 1 4 6 4 1第一层 1第二层 1 1第三层 1 2 1第四层 1 3 3 1 ……… 11 第五层 1 4 6 4 1第一层 1 第二层 1 1 第三层 1 2 1 第四层 1 3 3 1 ……… A B C D E F G ????? “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?AB3. 纵横路线图(我们把图顺时针转45度)1思维拓展:四、课堂小结你有什么收获!
(a+b)2=
(a+b)3=
(a+b)4=
(a+b)5=
(a+b)6=
1a+1b1a2+2ab+1b21a3+3a2b+3ab2+1b31a4+4a3b+6a2b2+4ab3+1b41a5+5a4b+10a3b2+10a2b3+5ab4+1b51a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6杨辉三角与二项展开式系数的关系(a+b)n 展开式的二项式系数表称为“杨辉三角”《详解九章算法》中记载的表杨辉三角与二项展开式系数的关系(a+b)n 展开式的二项式系数表称为“杨辉三角”1解决问题:如图,在由二项式系数所构成的杨辉三角形中,第 _____行中从左至右第14与第15个数的比为2:3.1.3.2杨辉三角议一议1)请看系数有没有明显的规律?2)上下两行有什么关系吗? 一、二项式系数性质:a).表中每行两端都是1。b).除1外的每一个数都等
于它肩上两个数的和。4+6=10总结提炼1:对称美总结提炼2: 与首末两端“等距离”的两个二项式系数相等当n为偶数:如2、4、6时,中间一项最大当n为奇数:如1、3、5时,中间两项最大总结提炼3:单调性与最值知识探究4:每一行的二项式系数的和等于?每一行的二项式系数的和等于 2 n 学以致用:方法赋值法学以致用:变式2:方法:求奇次项系数之和与偶次项系数的和
可以先赋值,然后解方程组整体求解赋值法二、杨辉三角的进一步探索1.杨辉三角的第2k-1行的各数字特点 第2k-1行(k是正整数)的各个数字都是奇数。第1行第6行第2行第3行第4行第5行第7行第0行12.第1行第6行第2行第3行第4行第5行第7行第0行所有行的第二个数构成等差数列3.第1行第6行第2行第3行第4行第5行第7行第0行所有行的第三个数都是三角形数4.古希腊数学家:1,3,6,10,15,21…这些数量的(石子),都可以排成三角形第1行第6行第2行第3行第4行第5行第7行第0行n行中的第i个数是斜行i-1中前n-1个数之和 第1行第6行第2行第3行第4行第5行第7行5.第0行三、欣赏有趣的杨辉三角 1,1,2,3,5,8,13,21,34,... 1.斐波那契“兔子繁殖问题”此数列{an}满足, a1=1,a2=1, 且an=an-1+an-2 (n≥3)
这就是著名的斐波那契数列. 中世纪意大利数学家斐波那契的传世之作《算术之法》中提出了一个饶有趣味的问题:假定一对刚出生的兔子一个月就能长成大兔子,再过一个月就开始生下一对小兔子,并且以后每个月都生一对小兔子.设所生一对兔子均为一雄一雌,且均无死亡.问一对刚出生的小兔一年内可以繁殖成多少对兔子? 从杨辉三角得到答案:1,1,2,3,5,8,13,21,34,... 13
8
5
3
2
1
1大自然中的斐波那契数列----树丫的数目大自然中的斐波那契数列---种子的排列(松果)1弹球游戏,小球向容器内跌落,碰到第一层阻挡物后向两侧跌落碰到第二层阻挡物,再向两侧跌落碰到第三层阻挡物,如此一直下跌最终小球落入底层。根据具体地区获的相应的奖品(AG区奖品最好,BF区奖品次之,CE区奖品第三,D 区奖品最差)。 A B C D E F G2. 弹球游戏1 华罗庚是这样解释:钢珠从每一通道通过的可能情况是:任何一层的左右两边的通道都只有一个可能情形,而其他任一个通道的可能情形,等于它左右肩上两个通道的可能情形相加。于是,钢珠通过每一层每个通道的可能情形是:第五层 1 4 6 4 1第一层 1第二层 1 1第三层 1 2 1第四层 1 3 3 1 ……… 11 第五层 1 4 6 4 1第一层 1 第二层 1 1 第三层 1 2 1 第四层 1 3 3 1 ……… A B C D E F G ????? “纵横路线图”是数学中的一类有趣的问题:如图是某城市的部分街道图,纵横各有五条路,如果从A处走到B处 (只能由北到南,由西向东),那么有多少种不同的走法?AB3. 纵横路线图(我们把图顺时针转45度)1思维拓展:四、课堂小结你有什么收获!
