北师大版数学九上1.1菱形的判定(二)课件 (16张PPT)
文档属性
| 名称 | 北师大版数学九上1.1菱形的判定(二)课件 (16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览




文档简介
课件16张PPT。第一章 特殊平行四边形
北师大版数学九年级上册§1.1 菱形的性质与判定(二)
1、菱形是如何定义的?
12、菱形具有哪些性质?12会用菱形的判定方法进行有关的论证和计算。理解并掌握菱形的判定方法;证明文字命题是真命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出相应的图形,并标上字母;
(3)结合图形,用几何符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(执“因”导“果”,执“果”
索“因”);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证
明过程;
(6)检查表达过程是否正确、完善。
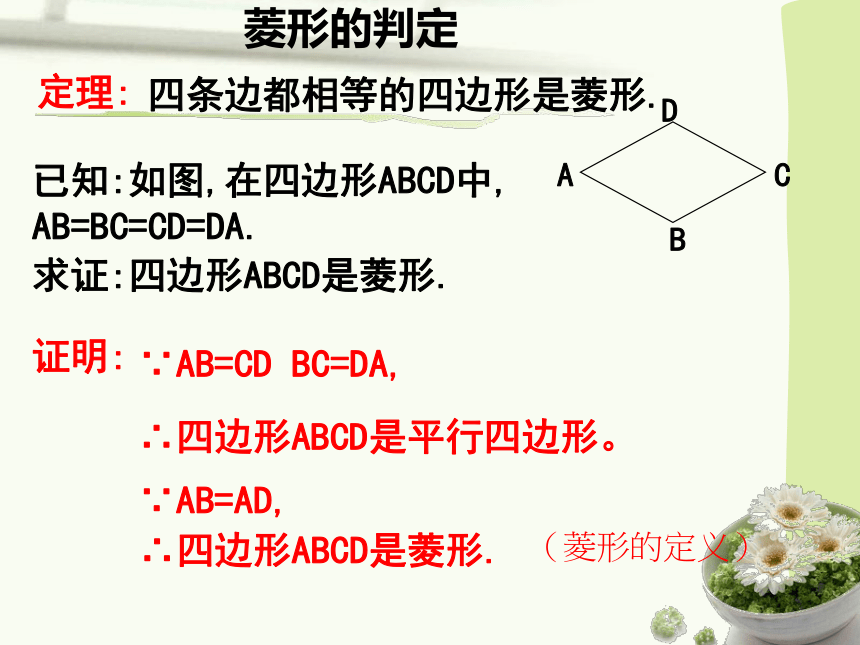
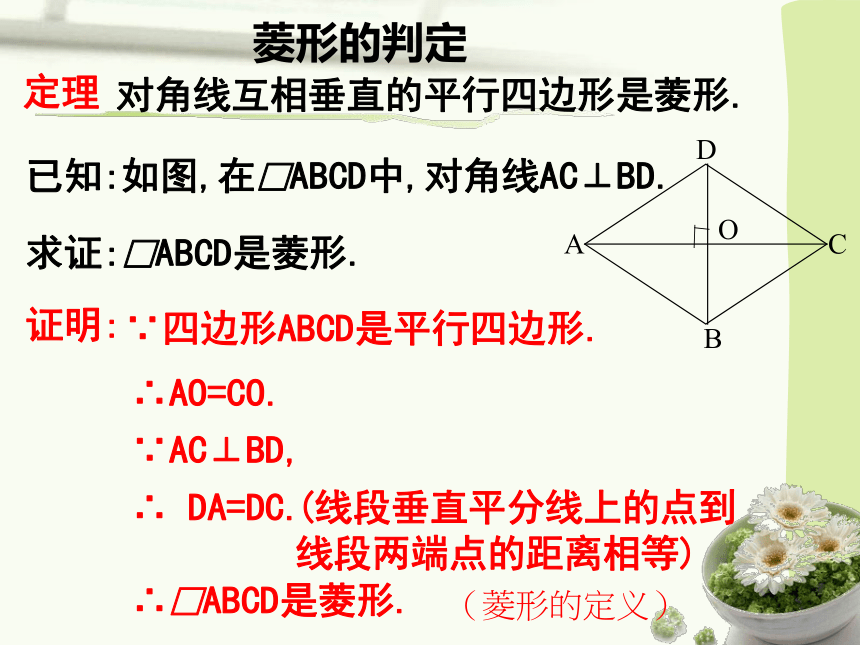
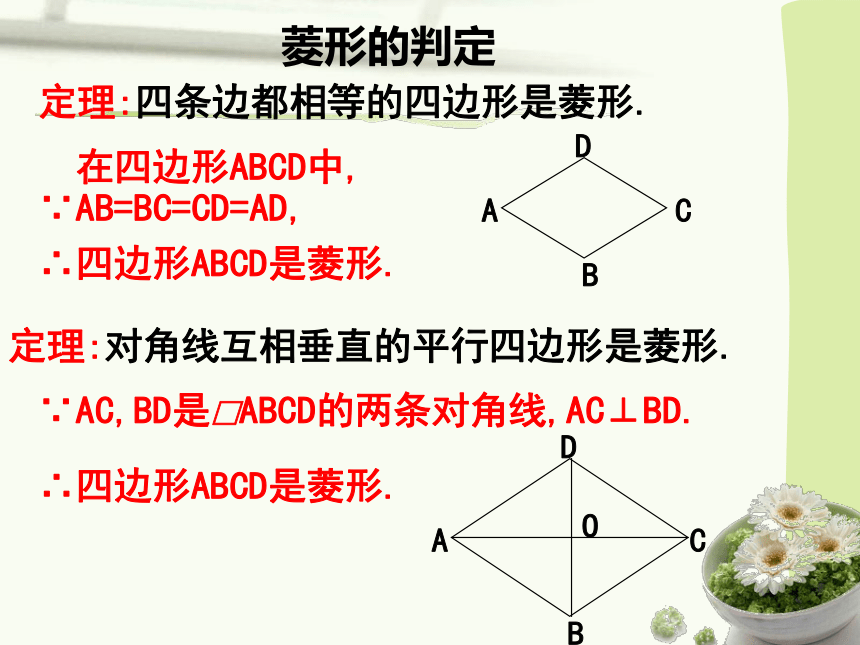
复 习 回 顾 菱形的判定 四条边都相等的四边形是菱形.已知:如图,在四边形ABCD中, AB=BC=CD=DA.证明:∵AB=CD BC=DA,∴四边形ABCD是平行四边形。求证:四边形ABCD是菱形.∵AB=AD,∴四边形ABCD是菱形.定理:(菱形的定义)菱形的判定对角线互相垂直的平行四边形是菱形.已知:如图,在□ABCD中,对角线AC⊥BD.求证:□ABCD是菱形.证明:∴AO=CO.∵AC⊥BD,∴ DA=DC.∵四边形ABCD是平行四边形.∴□ABCD是菱形.(线段垂直平分线上的点到线段两端点的距离相等)定理(菱形的定义)菱形的判定定理:四条边都相等的四边形是菱形.定理:对角线互相垂直的平行四边形是菱形. 在四边形ABCD中,
∵AB=BC=CD=AD,∴四边形ABCD是菱形.∵AC,BD是□ABCD的两条对角线,AC⊥BD.∴四边形ABCD是菱形.例2 如图,在 ABCD中,对角线AC与BD相交于点O,且AB= ,AO=2,BO=1.
求证: ABCD是菱形.
∴△AOB是直角三角形(勾股定理的逆定理)
即AC ⊥ BD,
∴证明: ∴ □ABCD是菱形.(对角线互相垂直的平行四边形是菱形.)
在△ABC中请你动脑筋 如何利用尺规画一个菱形? 通过本节课的学习,谈一谈你学会了什么?还有什么困惑?1、一组邻边相等的平行四边形是菱形.
2、四条边都相等的四边形是菱形.
3、对角线互相垂直的平行四边形是菱形.
4、对角线互相垂直平分的四边形是菱形. 知识方面:菱形的判定方法 数学方法:实验、观察、猜想、类比、逻辑推理。当堂检测 1、判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形.( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形.( )
×√××√√2.下列条件中,不能判定四边形ABCD为菱形的是( ).
A. AC⊥BD ,AC与BD互相平分
B. AB=BC=CD=DA
C. AB=BC,AD=CD,且AC ⊥BD
D. AB=CD,AD=BC,AC ⊥BDC3.画一个菱形,使它的两条对角线的长分别为4cm和6cm.P7页 习题1.2 1 、 2请你动脑筋 把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?与同桌交换意见,并解释为什么?B
北师大版数学九年级上册§1.1 菱形的性质与判定(二)
1、菱形是如何定义的?
12、菱形具有哪些性质?12会用菱形的判定方法进行有关的论证和计算。理解并掌握菱形的判定方法;证明文字命题是真命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出相应的图形,并标上字母;
(3)结合图形,用几何符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(执“因”导“果”,执“果”
索“因”);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证
明过程;
(6)检查表达过程是否正确、完善。
复 习 回 顾 菱形的判定 四条边都相等的四边形是菱形.已知:如图,在四边形ABCD中, AB=BC=CD=DA.证明:∵AB=CD BC=DA,∴四边形ABCD是平行四边形。求证:四边形ABCD是菱形.∵AB=AD,∴四边形ABCD是菱形.定理:(菱形的定义)菱形的判定对角线互相垂直的平行四边形是菱形.已知:如图,在□ABCD中,对角线AC⊥BD.求证:□ABCD是菱形.证明:∴AO=CO.∵AC⊥BD,∴ DA=DC.∵四边形ABCD是平行四边形.∴□ABCD是菱形.(线段垂直平分线上的点到线段两端点的距离相等)定理(菱形的定义)菱形的判定定理:四条边都相等的四边形是菱形.定理:对角线互相垂直的平行四边形是菱形. 在四边形ABCD中,
∵AB=BC=CD=AD,∴四边形ABCD是菱形.∵AC,BD是□ABCD的两条对角线,AC⊥BD.∴四边形ABCD是菱形.例2 如图,在 ABCD中,对角线AC与BD相交于点O,且AB= ,AO=2,BO=1.
求证: ABCD是菱形.
∴△AOB是直角三角形(勾股定理的逆定理)
即AC ⊥ BD,
∴证明: ∴ □ABCD是菱形.(对角线互相垂直的平行四边形是菱形.)
在△ABC中请你动脑筋 如何利用尺规画一个菱形? 通过本节课的学习,谈一谈你学会了什么?还有什么困惑?1、一组邻边相等的平行四边形是菱形.
2、四条边都相等的四边形是菱形.
3、对角线互相垂直的平行四边形是菱形.
4、对角线互相垂直平分的四边形是菱形. 知识方面:菱形的判定方法 数学方法:实验、观察、猜想、类比、逻辑推理。当堂检测 1、判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形.( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形.( )
×√××√√2.下列条件中,不能判定四边形ABCD为菱形的是( ).
A. AC⊥BD ,AC与BD互相平分
B. AB=BC=CD=DA
C. AB=BC,AD=CD,且AC ⊥BD
D. AB=CD,AD=BC,AC ⊥BDC3.画一个菱形,使它的两条对角线的长分别为4cm和6cm.P7页 习题1.2 1 、 2请你动脑筋 把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?与同桌交换意见,并解释为什么?B
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
