23.2.3 方向角问题 教案(表格式)
文档属性
| 名称 | 23.2.3 方向角问题 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 50.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览

文档简介
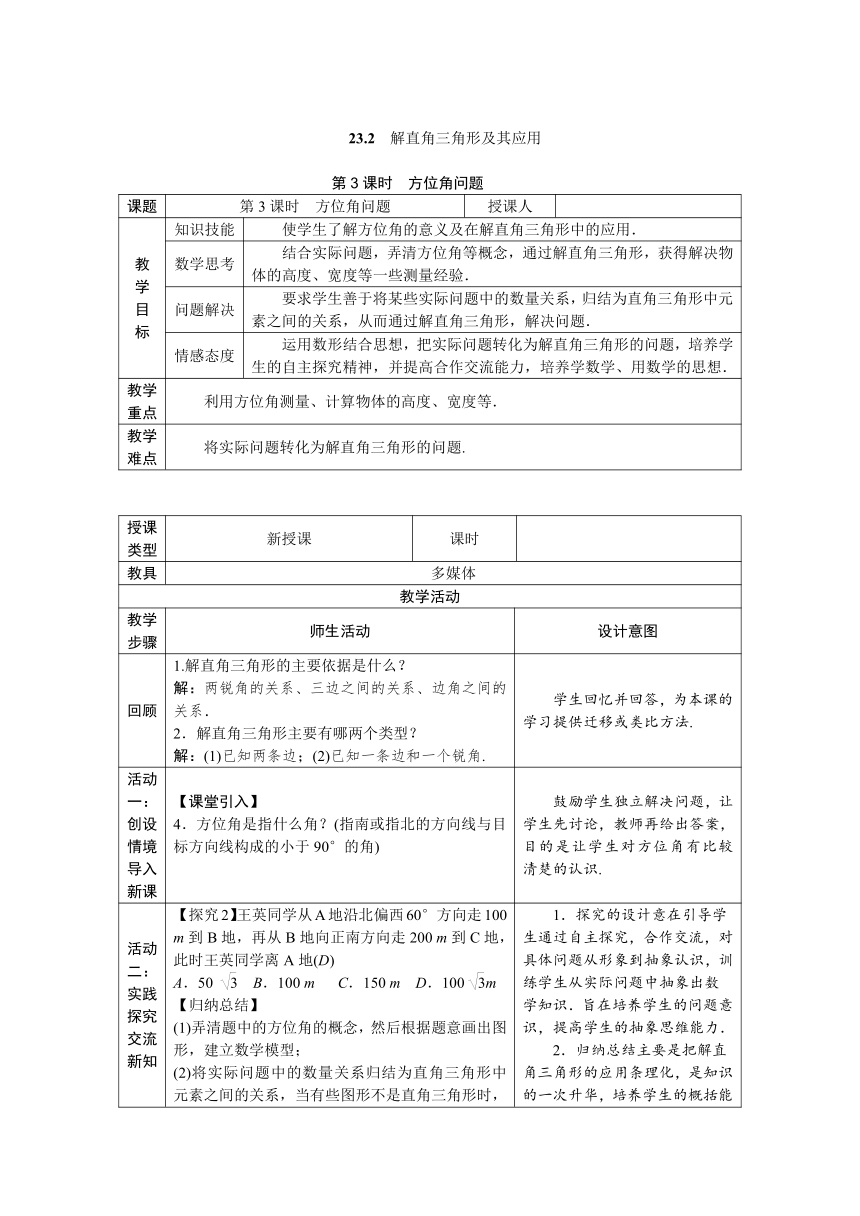
23.2 解直角三角形及其应用
第3课时 方位角问题
课题
第3课时 方位角问题
授课人
教
学
目
标
知识技能
使学生了解方位角的意义及在解直角三角形中的应用.
数学思考
结合实际问题,弄清方位角等概念,通过解直角三角形,获得解决物体的高度、宽度等一些测量经验.
问题解决
要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而通过解直角三角形,解决问题.
情感态度
运用数形结合思想,把实际问题转化为解直角三角形的问题,培养学生的自主探究精神,并提高合作交流能力,培养学数学、用数学的思想.
教学重点
利用方位角测量、计算物体的高度、宽度等.
教学难点
将实际问题转化为解直角三角形的问题.
授课
类型
新授课
课时
教具
多媒体
教学活动
教学
步骤
师生活动
设计意图
回顾
1.解直角三角形的主要依据是什么?
解:两锐角的关系、三边之间的关系、边角之间的关系.
2.解直角三角形主要有哪两个类型?
解:(1)已知两条边;(2)已知一条边和一个锐角.
学生回忆并回答,为本课的学习提供迁移或类比方法.
活动
一:
创设
情境
导入
新课
【课堂引入】
4.方位角是指什么角?(指南或指北的方向线与目标方向线构成的小于90°的角)
鼓励学生独立解决问题,让学生先讨论,教师再给出答案,目的是让学生对方位角有比较清楚的认识.
活动
二:
实践
探究
交流
新知
【探究2】王英同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时王英同学离A地(D)
A.50 B.100 m C.150 m D.100 m
【归纳总结】
(1)弄清题中的方位角的概念,然后根据题意画出图形,建立数学模型;
(2)将实际问题中的数量关系归结为直角三角形中元素之间的关系,当有些图形不是直角三角形时,可适当添加辅助线,把它们分割成直角三角形或矩形;
(3)解非直角三角形常作的辅助线:①通过作高构造直角三角形;②利用图形本身的性质,如等腰三角形顶角平分线垂直于底边.
1.探究的设计意在引导学生通过自主探究,合作交流,对具体问题从形象到抽象认识,训练学生从实际问题中抽象出数学知识.旨在培养学生的问题意识,提高学生的抽象思维能力.
2.归纳总结主要是把解直角三角形的应用条理化,是知识的一次升华,培养学生的概括能力,突出教学重点.
活动
三:
开放
训练
体现
应用
【应用举例】
例 [十堰] 如图23-2-51,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是__24海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)
图23-2-51
1.审题是解题的关键,通过运用解直角三角形的概念,学会解决简单的问题.采取启发式教学发挥学生的潜能.
2.例题考查了解直角三角形的应用——方位角,解题的关键是把△ABC转化为含特殊角的直角三角形.
(续表)
活动
四:
课堂
总结
反思
【当堂训练】
1.课本P126中的练习.
2.课本P128中的练习.
当堂检测,及时反馈学习效果.
【知识网络】
1.方位角
图23-2-55
2.实际问题通过添加辅助线转化为解直角三角形的问题.
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
本课时在新课引入时应用了学生熟悉的校园生活为背景,提出了本节课要用到的方位角,并对这三种角作了简单的描述,学生应用时应该是水到渠成的效果.
②[讲授效果反思]
应用方位角解决解直角三角形中的问题是本节课的重点,比较基础,希望师生共同了解仰角、俯角和方位角的初步应用,建议每道例题学生先做,然后教师再用多媒体展示答案,突出学生的主体地位和教师的主导作用.
③[师生互动反思]
________________________________________________
________________________________________________
④[习题反思]
好题题号__________________________________________
错题题号__________________________________________
反思,更进一步提升.
