沪科版九年级上册21.1 二次函数 教案(表格式)
文档属性
| 名称 | 沪科版九年级上册21.1 二次函数 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 111.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览

文档简介
第21章 二次函数与反比例函数
主题
二次函数与反比例函数
课型
新授课
上课时间
教学内容
21.1 二次函数;21.2 二次函数的图象和性质;21.3 二次函数与一元二次方程;21.4 二次函数的应用;21.5 反比例函数;21.6 综合实践 获取最大利润
教材分析
本章对二次函数和反比例函数的学习,进一步丰富了研究函数的内容和方法,搞好这部分内容的教学,对进入高中后,学生对初等函数的学习有重要的意义.
教学目标
1.知识与技能
了解二次函数和反比例函数的意义;掌握二次函数和反比例函数图象的画法;理解二次函数顶点坐标及最大值和最小值的意义;会根据不同的条件, 确定二次函数或反比例函数的解析式,会用待定系数法;会把一些实际问题归结为二次函数或反比例函数问题,并会运用二次函数或反比例函数的性质加以解决.
2.过程与方法
(1)通过对实际问题情境的分析确定二次函数、反比例函数的表达式,并体会二次函数、反比例函数的意义;(2)会用描点法画出二次函数、反比例函数的图象,能从图象上认识二次函数、反比例函数的性质;(3)会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导),并能解决简单的实际问题;(4)会利用二次函数的图象求一元二次方程的近似解;(5)能用反比例函数解决某些实际问题.
3.情感、态度与价值观
从学生感兴趣的问题入手,能使学生积极参与数学学习活动,对数学有好奇心和求知欲.把数学问题和实际问题相联系,使学生初步体会数学与人类生活的密切联系及对人类历史发展的作用.通过学生之间互相交流合作,让学生学会与人合作,并能与他人交流思维的过程,培养大家的合作意识.
教学
重难点
重点:
1.二次函数和反比例函数的概念.
2.二次函数和反比例函数图象和性质,以及它们的应用.
3.培养学生在解决实际问题时建立函数模型的意识,并掌握建立函数模型的技能.
难点:
1.二次函数和反比例函数图象和性质,以及它们的应用.
2.解决实际问题时建立函数模型的意识,并掌握建立函数模型的技能.
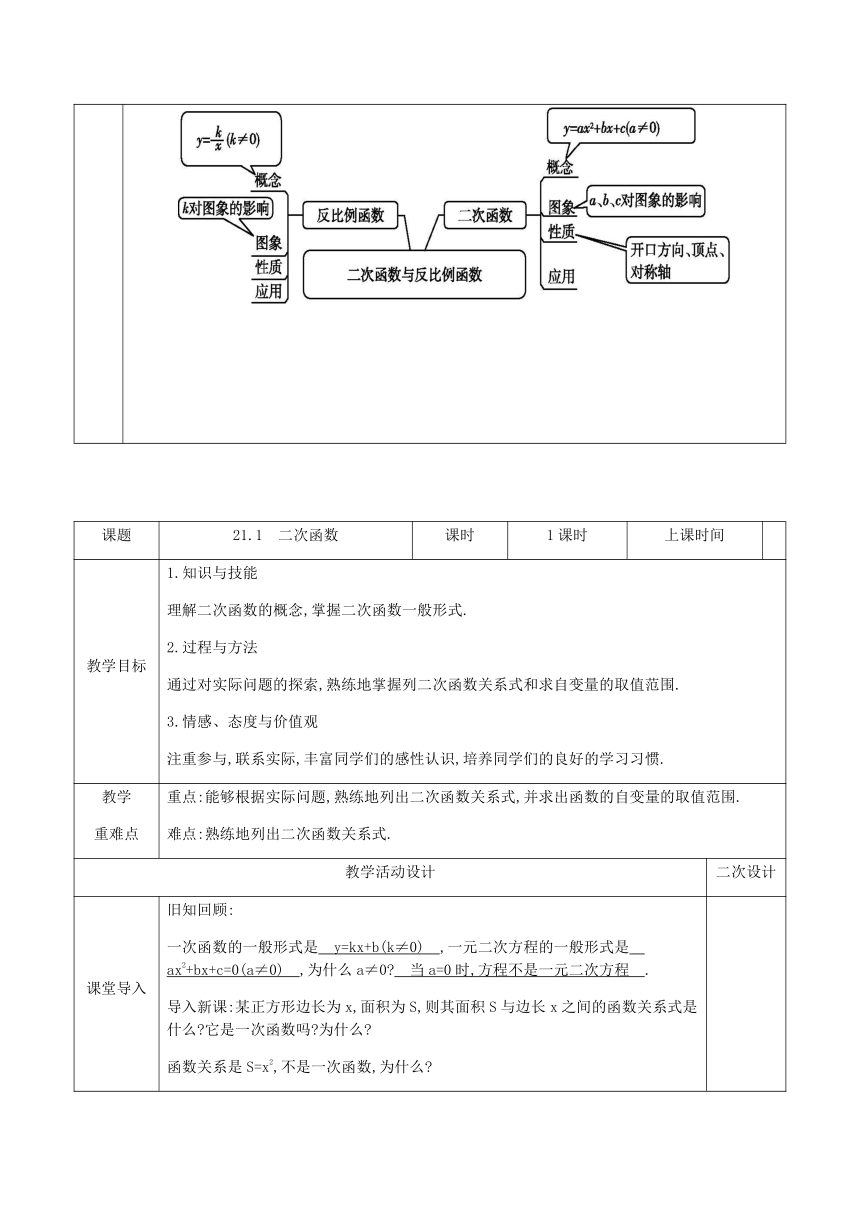
知识结构
/
课题
21.1 二次函数
课时
1课时
上课时间
教学目标
1.知识与技能
理解二次函数的概念,掌握二次函数一般形式.
2.过程与方法
通过对实际问题的探索,熟练地掌握列二次函数关系式和求自变量的取值范围.
3.情感、态度与价值观
注重参与,联系实际,丰富同学们的感性认识,培养同学们的良好的学习习惯.
教学
重难点
重点:能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围.
难点:熟练地列出二次函数关系式.
教学活动设计
二次设计
课堂导入
旧知回顾:
一次函数的一般形式是 y=kx+b(k≠0) ,一元二次方程的一般形式是 ax2+bx+c=0(a≠0) ,为什么a≠0? 当a=0时,方程不是一元二次方程 .?
导入新课:某正方形边长为x,面积为S,则其面积S与边长x之间的函数关系式是什么?它是一次函数吗?为什么?
函数关系是S=x2,不是一次函数,为什么?
探索新知
合作探究
自学指导
知识模块一 二次函数的概念
阅读教材本课时的内容,回答以下问题:
1.问题①中40 m是长方形的周长吗? 是 ,矩形面积S与其一边长x之间的函数关系式为 S=x(20-x)(02.问题②中,设增加x人,此时,共有 15+x 个装配工,每人每天可少装配 10x 个玩具,因此每人每天只装配 190-10x 个玩具,所以,增加人数后,每天装配玩具总数y可表示为 y=(190-10x)(15+x) .?
这个函数是一次函数吗? 不是 ,原因: 右边不是x的一次式 .?
知识模块二 在实际问题中列二次函数的解析式
【例题】 列出下列函数的关系式.
(1)一个圆柱的高等于底面半径的2倍,则它的表面积S与底面半径r之间的关系式为 S=6πr2 .?
(2)某工厂一种产品现在年产量是20件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示? y=20(1+x)2 .?
学生看书,教师巡视,督促每一位学生认真自学,鼓励学生质疑问难.
探索新知
合作探究
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.让学生归纳上面两个函数解析式具有哪些共同特征?
3.思考:解决列函数关系式这一类题的步骤.
教师指导
1.易错点:
二次函数是自变量的多项式,自变量的最高次数都是2,二次项系数不为0.
2.归纳小结:
一般地,表达式形如 y=ax2+bx+c (a,b,c是常数,且a≠0)的函数叫做x的二次函数,其中x是自变量,a为 二次项系数 ,b为 一次项系数 ,c为 常数项 .?
3.方法规律:
(1) 二次函数必须满足三个条件:①函数解析式必须是整式;②化简后自变量的最高次数必须是2;③二次项系数不为0.
(2) 解决列函数关系式这一类题的步骤:①审清题意,②找等量关系,③列函数关系式.
当堂训练
1.函数y=-2x2+3x-1的二次项系数、一次项系数、常数项依次是( )
(A)-2,3,1 (B)-2,3,-1 (C)2,3,1 (D)2,3,-1
2.将一根长为20 cm的铁丝弯成一个矩形框架,设矩形的一边长为x cm,面积为y cm2,则y与x之间的函数关系式为 ,其中自变量x的取值范围是 .?
3.某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为 .?
板书设计
21.1 二次函数
知识模块一 二次函数的概念
知识模块二 在实际问题中列二次函数的解析式
教学反思
主题
二次函数与反比例函数
课型
新授课
上课时间
教学内容
21.1 二次函数;21.2 二次函数的图象和性质;21.3 二次函数与一元二次方程;21.4 二次函数的应用;21.5 反比例函数;21.6 综合实践 获取最大利润
教材分析
本章对二次函数和反比例函数的学习,进一步丰富了研究函数的内容和方法,搞好这部分内容的教学,对进入高中后,学生对初等函数的学习有重要的意义.
教学目标
1.知识与技能
了解二次函数和反比例函数的意义;掌握二次函数和反比例函数图象的画法;理解二次函数顶点坐标及最大值和最小值的意义;会根据不同的条件, 确定二次函数或反比例函数的解析式,会用待定系数法;会把一些实际问题归结为二次函数或反比例函数问题,并会运用二次函数或反比例函数的性质加以解决.
2.过程与方法
(1)通过对实际问题情境的分析确定二次函数、反比例函数的表达式,并体会二次函数、反比例函数的意义;(2)会用描点法画出二次函数、反比例函数的图象,能从图象上认识二次函数、反比例函数的性质;(3)会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导),并能解决简单的实际问题;(4)会利用二次函数的图象求一元二次方程的近似解;(5)能用反比例函数解决某些实际问题.
3.情感、态度与价值观
从学生感兴趣的问题入手,能使学生积极参与数学学习活动,对数学有好奇心和求知欲.把数学问题和实际问题相联系,使学生初步体会数学与人类生活的密切联系及对人类历史发展的作用.通过学生之间互相交流合作,让学生学会与人合作,并能与他人交流思维的过程,培养大家的合作意识.
教学
重难点
重点:
1.二次函数和反比例函数的概念.
2.二次函数和反比例函数图象和性质,以及它们的应用.
3.培养学生在解决实际问题时建立函数模型的意识,并掌握建立函数模型的技能.
难点:
1.二次函数和反比例函数图象和性质,以及它们的应用.
2.解决实际问题时建立函数模型的意识,并掌握建立函数模型的技能.
知识结构
/
课题
21.1 二次函数
课时
1课时
上课时间
教学目标
1.知识与技能
理解二次函数的概念,掌握二次函数一般形式.
2.过程与方法
通过对实际问题的探索,熟练地掌握列二次函数关系式和求自变量的取值范围.
3.情感、态度与价值观
注重参与,联系实际,丰富同学们的感性认识,培养同学们的良好的学习习惯.
教学
重难点
重点:能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围.
难点:熟练地列出二次函数关系式.
教学活动设计
二次设计
课堂导入
旧知回顾:
一次函数的一般形式是 y=kx+b(k≠0) ,一元二次方程的一般形式是 ax2+bx+c=0(a≠0) ,为什么a≠0? 当a=0时,方程不是一元二次方程 .?
导入新课:某正方形边长为x,面积为S,则其面积S与边长x之间的函数关系式是什么?它是一次函数吗?为什么?
函数关系是S=x2,不是一次函数,为什么?
探索新知
合作探究
自学指导
知识模块一 二次函数的概念
阅读教材本课时的内容,回答以下问题:
1.问题①中40 m是长方形的周长吗? 是 ,矩形面积S与其一边长x之间的函数关系式为 S=x(20-x)(0
这个函数是一次函数吗? 不是 ,原因: 右边不是x的一次式 .?
知识模块二 在实际问题中列二次函数的解析式
【例题】 列出下列函数的关系式.
(1)一个圆柱的高等于底面半径的2倍,则它的表面积S与底面半径r之间的关系式为 S=6πr2 .?
(2)某工厂一种产品现在年产量是20件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示? y=20(1+x)2 .?
学生看书,教师巡视,督促每一位学生认真自学,鼓励学生质疑问难.
探索新知
合作探究
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.让学生归纳上面两个函数解析式具有哪些共同特征?
3.思考:解决列函数关系式这一类题的步骤.
教师指导
1.易错点:
二次函数是自变量的多项式,自变量的最高次数都是2,二次项系数不为0.
2.归纳小结:
一般地,表达式形如 y=ax2+bx+c (a,b,c是常数,且a≠0)的函数叫做x的二次函数,其中x是自变量,a为 二次项系数 ,b为 一次项系数 ,c为 常数项 .?
3.方法规律:
(1) 二次函数必须满足三个条件:①函数解析式必须是整式;②化简后自变量的最高次数必须是2;③二次项系数不为0.
(2) 解决列函数关系式这一类题的步骤:①审清题意,②找等量关系,③列函数关系式.
当堂训练
1.函数y=-2x2+3x-1的二次项系数、一次项系数、常数项依次是( )
(A)-2,3,1 (B)-2,3,-1 (C)2,3,1 (D)2,3,-1
2.将一根长为20 cm的铁丝弯成一个矩形框架,设矩形的一边长为x cm,面积为y cm2,则y与x之间的函数关系式为 ,其中自变量x的取值范围是 .?
3.某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为 .?
板书设计
21.1 二次函数
知识模块一 二次函数的概念
知识模块二 在实际问题中列二次函数的解析式
教学反思
