沪科版24.7.1 弧长与扇形面积课件(32张PPT)
文档属性
| 名称 | 沪科版24.7.1 弧长与扇形面积课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览





文档简介
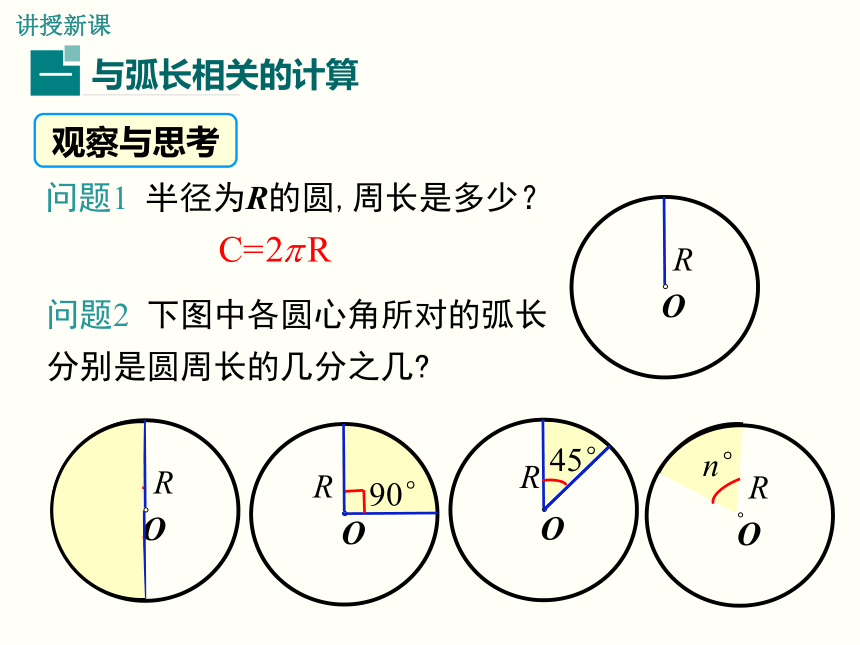
课件32张PPT。24.7 弧长与扇形面积第1课时 弧长与扇形面积第24章 圆学习目标1. 理解弧长和扇形面积公式的探求过程.(难点)
2. 会利用弧长和扇形面积的计算公式进行计算.
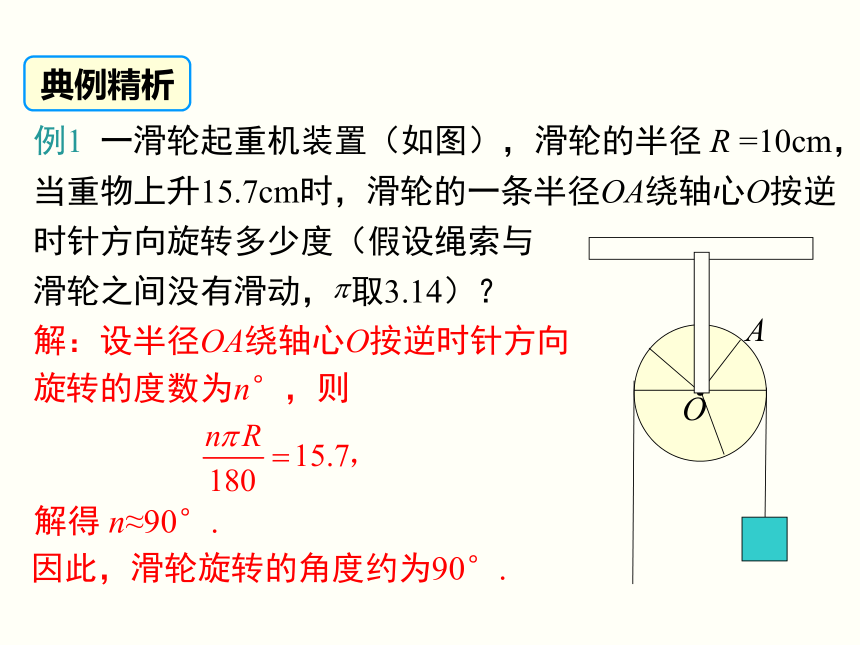
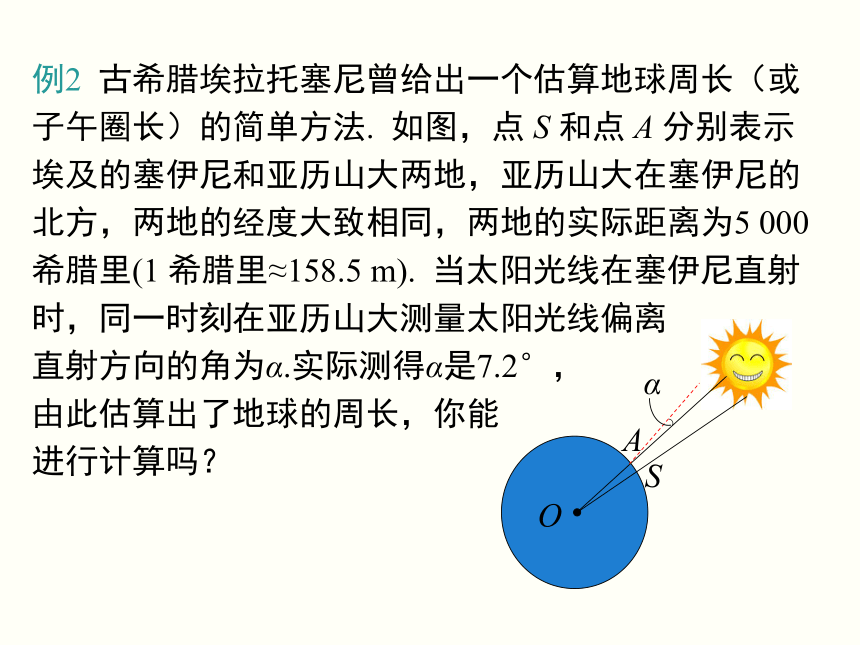
(重点) 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?怎样来计算弯道的“展直长度”?因为要保证这些弯道的“展直长度”是一样的.导入新课讲授新课问题1 半径为R的圆,周长是多少?问题2 下图中各圆心角所对的弧长分别是圆周长的几分之几?观察与思考注意:用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.算一算 已知弧所对的圆心角为60°,半径是4,则弧长为知识要点弧长公式解:设半径OA绕轴心O按逆时针方向旋转的度数为n°,则解得 n≈90°.因此,滑轮旋转的角度约为90°.典例精析例2 古希腊埃拉托塞尼曾给出一个估算地球周长(或子午圈长)的简单方法. 如图,点 S 和点 A 分别表示埃及的塞伊尼和亚历山大两地,亚历山大在塞伊尼的北方,两地的经度大致相同,两地的实际距离为5 000希腊里(1 希腊里≈158.5 m). 当太阳光线在塞伊尼直射时,同一时刻在亚历山大测量太阳光线偏离
直射方向的角为α.实际测得α是7.2°,
由此估算出了地球的周长,你能
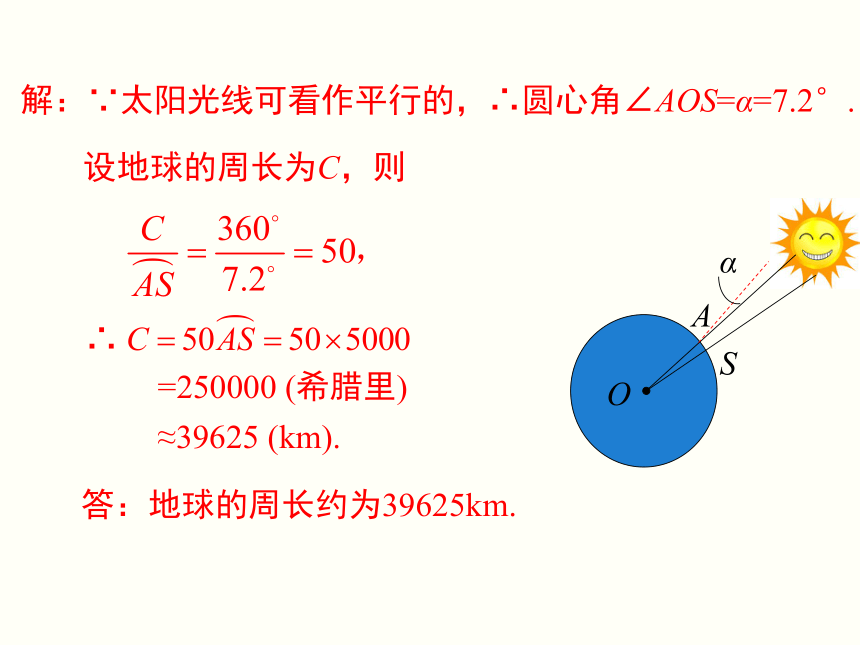
进行计算吗?解:∵太阳光线可看作平行的,∴圆心角∠AOS=α=7.2°.设地球的周长为C,则答:地球的周长约为39625km.=250000 (希腊里)
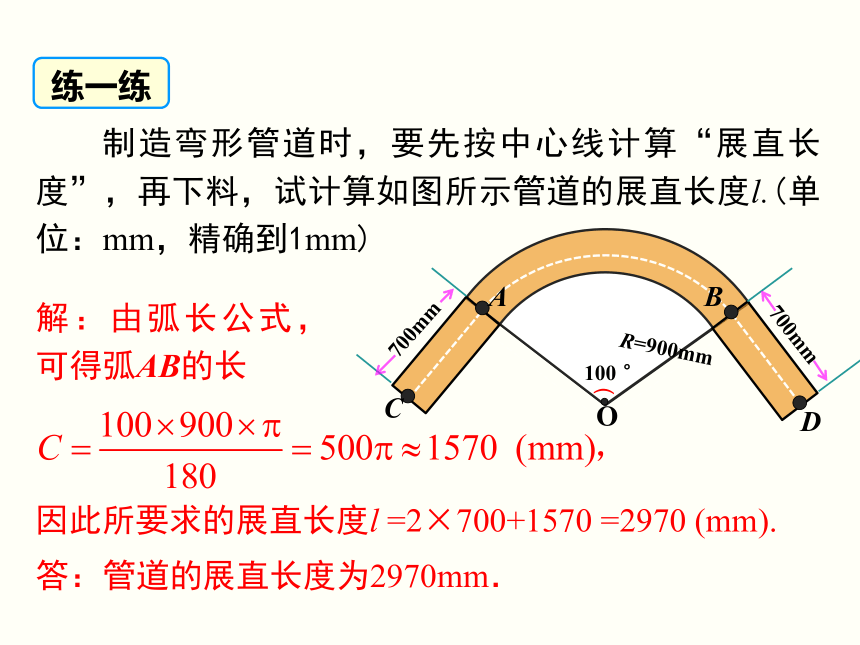
≈39625 (km). 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度l.(单位:mm,精确到1mm)
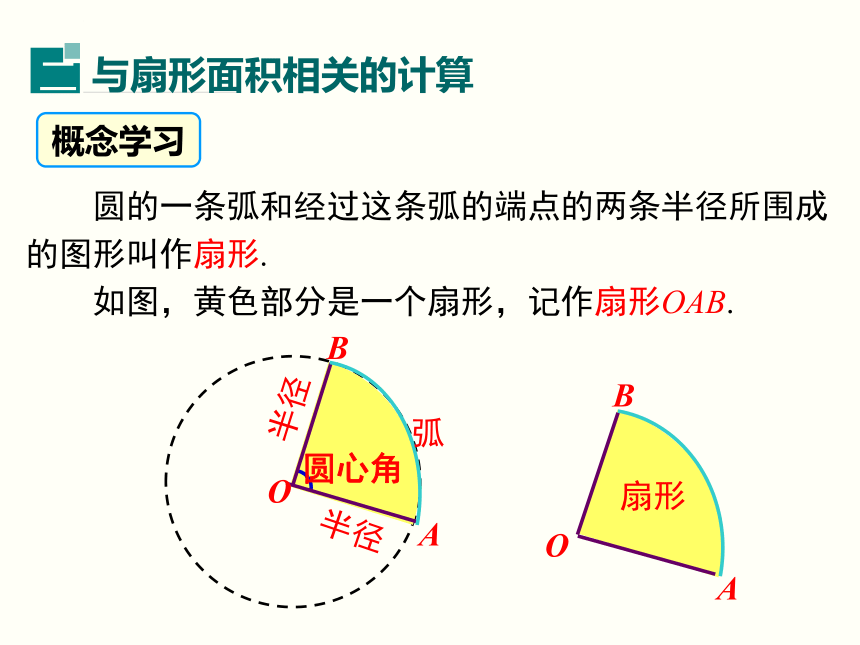
解:由弧长公式,可得弧AB的长因此所要求的展直长度l =2×700+1570 =2970 (mm). 答:管道的展直长度为2970mm. 练一练 圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
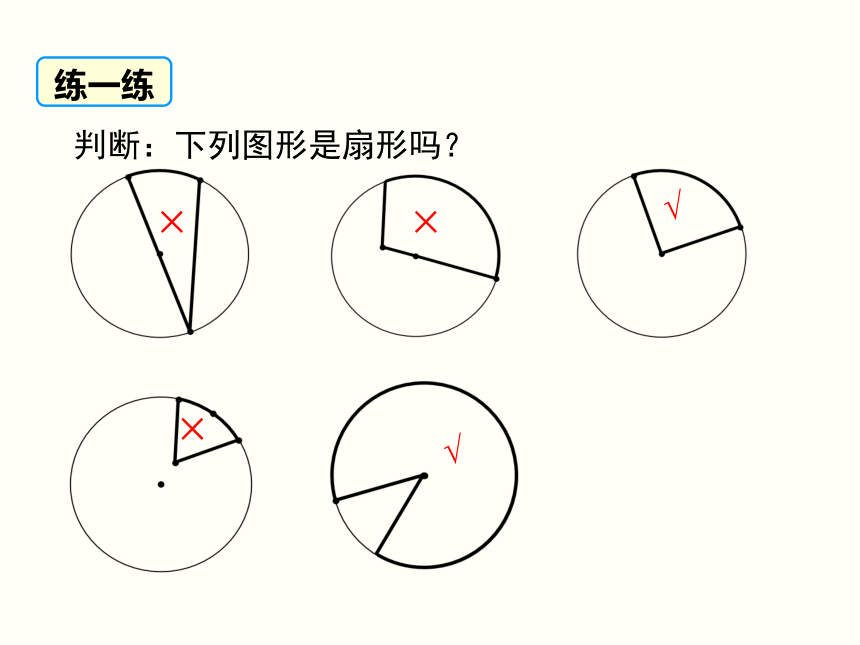
如图,黄色部分是一个扇形,记作扇形OAB.OBA圆心角概念学习判断:下列图形是扇形吗?√×××√练一练合作探究问题1 半径为r的圆,面积是多少?问题2 下图中各扇形面积分别是圆面积的几分之几,具体是多少呢?=半径为r的圆中,圆心角为n°的扇形的面积 ①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).知识要点 ___大小不变时,对应的扇形面积与 __ 有关,
___ 越长,面积越大.圆心角半径半径圆的 不变时,扇形面积与 有关, 越大,面积越大.圆心角半径 圆心角 总结:扇形的面积与圆心角、半径有关.问题 扇形的面积与哪些因素有关?问题 扇形的弧长公式与面积公式有联系吗? 想一想 扇形的面积公式与什么公式类似? 例3 如图,圆心角为60°的扇形的半径为10cm.求这个扇形的面积和周长.(精确到0.01cm2和0.01cm)解:∵n=60,r=10cm,
∴扇形的面积为扇形的周长为2. 已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇= .练一练例4 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;证明:连接OC,如图.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠ACO=∠A=30°.
∴∠OCD=180°-∠A-∠D-∠ACO=90°.
即OC⊥CD,
∴CD是⊙O的切线.
(2)若⊙O的半径为2,求图中阴影部分的面积.解:∵∠A=30°,∴∠COB=2∠A=60°,在Rt△OCD中,例5 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm) 讨论:(1)截面上有水部分的面积是指图上哪一部分?阴影部分.D(2)(3)(2) 水面高0.3 m是指哪一条线段的长?这条线段应该怎样画出来?线段DC. 过点O作OD垂直符号于AB并长交圆O于C.(3) 要求图中阴影部分面积,应该怎么办?阴影部分面积 = 扇形OAB的面积 - △OAB 的面积解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.∵ OC=0.6,DC=0.3, ∴ OD=OC- DC=0.3,∴ OD=DC.又 AD ⊥DC,∴ AD是线段OC的垂直平分线,∴ AC=AO=OC. 从而 ∠AOD=60?,∠AOB=120?. 有水部分的面积: S =S扇形OAB - SΔOAB弓形的面积=扇形的面积±三角形的面积S弓形=S扇形-S三角形S弓形=S扇形+S三角形知识要点弓形的面积公式 当堂练习C3.如图,☉A、☉B、 ☉C、 ☉D两两不相交,且半径都是2cm,则图中阴影部分的面积是 .解析:点A所经过的路线的长为三个半径为2,圆心角为120°的扇形弧长与两个半径为 ,圆心角为90°的扇形弧长之和,即 5. 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.ABDCE6. 如图,一个边长为10cm的等边三角形模板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A'B'C的位置,求顶点A从开始到结束所经过的路程为多少.解:由图可知,由于∠A'CB'=60°,则等边三角形木板绕点C按顺时针方向旋转了120°,即∠ACA' =120°,这说明顶点A经过的路程长等于弧AA' 的长.
∵等边三角形ABC的边长为10cm,
∴弧AA' 所在圆的半径为10cm.
∴l弧AA' 答:顶点A从开始到结束时所经过的路程为课堂小结弧长扇形定义公式阴影部分面积
求法:整体思想弓形公式S弓形=S扇形-S三角形
S弓形=S扇形+S三角形割补法公式
2. 会利用弧长和扇形面积的计算公式进行计算.
(重点) 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?怎样来计算弯道的“展直长度”?因为要保证这些弯道的“展直长度”是一样的.导入新课讲授新课问题1 半径为R的圆,周长是多少?问题2 下图中各圆心角所对的弧长分别是圆周长的几分之几?观察与思考注意:用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.算一算 已知弧所对的圆心角为60°,半径是4,则弧长为知识要点弧长公式解:设半径OA绕轴心O按逆时针方向旋转的度数为n°,则解得 n≈90°.因此,滑轮旋转的角度约为90°.典例精析例2 古希腊埃拉托塞尼曾给出一个估算地球周长(或子午圈长)的简单方法. 如图,点 S 和点 A 分别表示埃及的塞伊尼和亚历山大两地,亚历山大在塞伊尼的北方,两地的经度大致相同,两地的实际距离为5 000希腊里(1 希腊里≈158.5 m). 当太阳光线在塞伊尼直射时,同一时刻在亚历山大测量太阳光线偏离
直射方向的角为α.实际测得α是7.2°,
由此估算出了地球的周长,你能
进行计算吗?解:∵太阳光线可看作平行的,∴圆心角∠AOS=α=7.2°.设地球的周长为C,则答:地球的周长约为39625km.=250000 (希腊里)
≈39625 (km). 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度l.(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长因此所要求的展直长度l =2×700+1570 =2970 (mm). 答:管道的展直长度为2970mm. 练一练 圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图,黄色部分是一个扇形,记作扇形OAB.OBA圆心角概念学习判断:下列图形是扇形吗?√×××√练一练合作探究问题1 半径为r的圆,面积是多少?问题2 下图中各扇形面积分别是圆面积的几分之几,具体是多少呢?=半径为r的圆中,圆心角为n°的扇形的面积 ①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).知识要点 ___大小不变时,对应的扇形面积与 __ 有关,
___ 越长,面积越大.圆心角半径半径圆的 不变时,扇形面积与 有关, 越大,面积越大.圆心角半径 圆心角 总结:扇形的面积与圆心角、半径有关.问题 扇形的面积与哪些因素有关?问题 扇形的弧长公式与面积公式有联系吗? 想一想 扇形的面积公式与什么公式类似? 例3 如图,圆心角为60°的扇形的半径为10cm.求这个扇形的面积和周长.(精确到0.01cm2和0.01cm)解:∵n=60,r=10cm,
∴扇形的面积为扇形的周长为2. 已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇= .练一练例4 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;证明:连接OC,如图.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠ACO=∠A=30°.
∴∠OCD=180°-∠A-∠D-∠ACO=90°.
即OC⊥CD,
∴CD是⊙O的切线.
(2)若⊙O的半径为2,求图中阴影部分的面积.解:∵∠A=30°,∴∠COB=2∠A=60°,在Rt△OCD中,例5 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm) 讨论:(1)截面上有水部分的面积是指图上哪一部分?阴影部分.D(2)(3)(2) 水面高0.3 m是指哪一条线段的长?这条线段应该怎样画出来?线段DC. 过点O作OD垂直符号于AB并长交圆O于C.(3) 要求图中阴影部分面积,应该怎么办?阴影部分面积 = 扇形OAB的面积 - △OAB 的面积解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.∵ OC=0.6,DC=0.3, ∴ OD=OC- DC=0.3,∴ OD=DC.又 AD ⊥DC,∴ AD是线段OC的垂直平分线,∴ AC=AO=OC. 从而 ∠AOD=60?,∠AOB=120?. 有水部分的面积: S =S扇形OAB - SΔOAB弓形的面积=扇形的面积±三角形的面积S弓形=S扇形-S三角形S弓形=S扇形+S三角形知识要点弓形的面积公式 当堂练习C3.如图,☉A、☉B、 ☉C、 ☉D两两不相交,且半径都是2cm,则图中阴影部分的面积是 .解析:点A所经过的路线的长为三个半径为2,圆心角为120°的扇形弧长与两个半径为 ,圆心角为90°的扇形弧长之和,即 5. 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.ABDCE6. 如图,一个边长为10cm的等边三角形模板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A'B'C的位置,求顶点A从开始到结束所经过的路程为多少.解:由图可知,由于∠A'CB'=60°,则等边三角形木板绕点C按顺时针方向旋转了120°,即∠ACA' =120°,这说明顶点A经过的路程长等于弧AA' 的长.
∵等边三角形ABC的边长为10cm,
∴弧AA' 所在圆的半径为10cm.
∴l弧AA' 答:顶点A从开始到结束时所经过的路程为课堂小结弧长扇形定义公式阴影部分面积
求法:整体思想弓形公式S弓形=S扇形-S三角形
S弓形=S扇形+S三角形割补法公式
