北师大数学九上 第六章 第50课时回顾与思考 课件
文档属性
| 名称 | 北师大数学九上 第六章 第50课时回顾与思考 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 667.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-06 00:00:00 | ||
图片预览




文档简介
课件10张PPT。 第六单元 反比例函数第50课时 回顾与思考北师大版 九年级上册一、选择题
1.若反比例函数 的图象经过点(8,4),则函数 y=-kx 为( )
A.y=32x B.y=-32x C. D.
2.已知 P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数 的图象上的
三点,且 x1<x2<0<x3,则 y1,y2,y3 的大小关系是( )
A.y3<y2<y1 B.y1<y2<y3 C.y2<y1<y3 D.y2<y3<y1
BC一、选择题
3.某学校要种植一块面积为 100 m2 的长方形草坪,要求两边长均不小于5
m,则草坪的一边长为 y(单位:m)随另一边长 x(单位:m)的变化而变化
的图象可能是( )
4.如图所示,矩形 AOBC 的面积为 4,反比例函数 的图象的一支经过矩形
对角线的交点 P,则该反比例函数的解析式是( )
A.y= B.y= C.y= D.y=
CC二、填空题
5.如果菱形的面积为 35,对角线长分别是 x,y,那么 y 与 x 的函数关系式
是 ________.
6.已知 y 与 2x+1 成反比例,且当 x=1 时,y=2,那么,当 x=0 时,
y= _____ .
7.若反比例函数 的图象经过点(-1,2),则 k 的值为 ____ .
8.若点 A(m,-2)在反比例函数 的图象上,则当函数值 y≥-2 时,自
变量 x 的取值范围是_____________ .
6-3x≤-2 或 x>0二、填空题
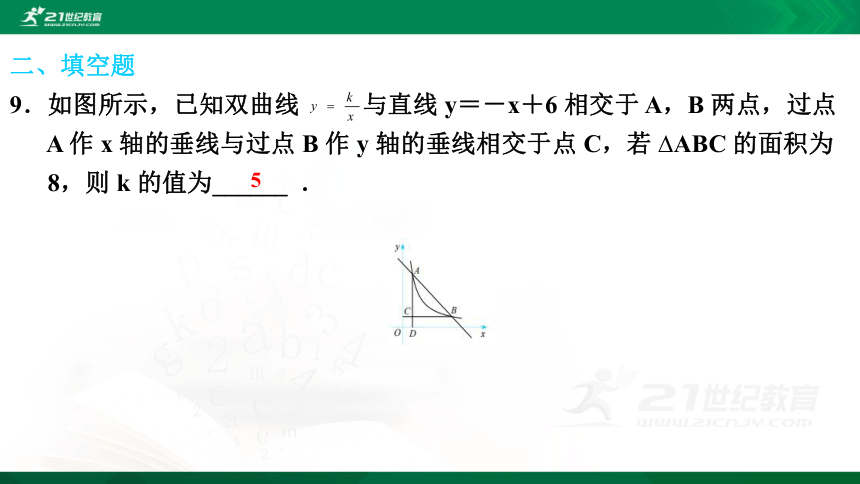
9.如图所示,已知双曲线 与直线 y=-x+6 相交于 A,B 两点,过点
A 作 x 轴的垂线与过点 B 作 y 轴的垂线相交于点 C,若 ?ABC 的面积为
8,则 k 的值为______ .5三、解答题
10.如图所示,□ABCD 放置在平面直角坐标系中,已知点 A(2,0),B(6,
0),D(0,3),反比例函数的图象经过点 C.
(1)求反比例函数的解析式;
【答案】(1)∵□ABCD 中,A(2,0),B(6,0),D(0,3),
∴AB=CD=4,DC∥AB,∴C(4,3).
设反比例解析式为 , 把 C 坐标代入得:k=12.
则反比例解析式为 .
三、解答题
10.如图所示,□ABCD 放置在平面直角坐标系中,已知点 A(2,0),B(6,
0),D(0,3),反比例函数的图象经过点 C.
(2)将□ABCD 向上平移,使点 B 恰好落在双曲线上,此时 A,B,C, D
的对应点分别为 A′,B′,C′,D′,且 C′D′与双曲线交于点 E,求线段
AA′的长及点 E 的坐标.
【答案】(2)如图所示,∵B(6,0),
∴把 x=6 代入反比例解析式得:y=2,即 B′(6,2).
∴平行四边形 ABCD 向上平移 2 个单位,即 AA′=2.
∴D′(0,5).
把 y=5 代入反比例解析式得: ,即
三、解答题
11.如图所示,已知反比例函数 的图象与一次函数 y2=ax+b 的图象交
于点 A(1,4)和点 B(m,-2).
(1)求这两个函数的表达式;
【答案】(1)∵函数 的图象过点 A(1,4),
即 ,∴k=4,即 .
又∵点 B(m,-2)在 上,
∴m=-2,∴B(-2,-2).
又∵一次函数 y2=ax+b 过 A,B 两点,
即 解得 ∴y2=2x+2.
综上可得 y1= 4x ,y2=2x+2. 三、解答题
11.如图所示,已知反比例函数 的图象与一次函数 y2=ax+b 的图象交
于点 A(1,4)和点 B(m,-2).
(2)观察图象,当 x>0 时,直接写出 y1>y2 时自变量 x 的取值范围;
(3)如果点 C 与点 A 关于 x 轴对称,求△ABC 的面积.
【答案】 (2)要使 y1>y2,即函数 y1 的图象总在函数 y2的图象上方,
∴x<-2 或 0<x<1.
(3)如图所示,过点 B 作 BD⊥AC 于点 D,
由图形及题意可得:AC=8,BD=3.
∴△ABC 的面积 谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.若反比例函数 的图象经过点(8,4),则函数 y=-kx 为( )
A.y=32x B.y=-32x C. D.
2.已知 P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数 的图象上的
三点,且 x1<x2<0<x3,则 y1,y2,y3 的大小关系是( )
A.y3<y2<y1 B.y1<y2<y3 C.y2<y1<y3 D.y2<y3<y1
BC一、选择题
3.某学校要种植一块面积为 100 m2 的长方形草坪,要求两边长均不小于5
m,则草坪的一边长为 y(单位:m)随另一边长 x(单位:m)的变化而变化
的图象可能是( )
4.如图所示,矩形 AOBC 的面积为 4,反比例函数 的图象的一支经过矩形
对角线的交点 P,则该反比例函数的解析式是( )
A.y= B.y= C.y= D.y=
CC二、填空题
5.如果菱形的面积为 35,对角线长分别是 x,y,那么 y 与 x 的函数关系式
是 ________.
6.已知 y 与 2x+1 成反比例,且当 x=1 时,y=2,那么,当 x=0 时,
y= _____ .
7.若反比例函数 的图象经过点(-1,2),则 k 的值为 ____ .
8.若点 A(m,-2)在反比例函数 的图象上,则当函数值 y≥-2 时,自
变量 x 的取值范围是_____________ .
6-3x≤-2 或 x>0二、填空题
9.如图所示,已知双曲线 与直线 y=-x+6 相交于 A,B 两点,过点
A 作 x 轴的垂线与过点 B 作 y 轴的垂线相交于点 C,若 ?ABC 的面积为
8,则 k 的值为______ .5三、解答题
10.如图所示,□ABCD 放置在平面直角坐标系中,已知点 A(2,0),B(6,
0),D(0,3),反比例函数的图象经过点 C.
(1)求反比例函数的解析式;
【答案】(1)∵□ABCD 中,A(2,0),B(6,0),D(0,3),
∴AB=CD=4,DC∥AB,∴C(4,3).
设反比例解析式为 , 把 C 坐标代入得:k=12.
则反比例解析式为 .
三、解答题
10.如图所示,□ABCD 放置在平面直角坐标系中,已知点 A(2,0),B(6,
0),D(0,3),反比例函数的图象经过点 C.
(2)将□ABCD 向上平移,使点 B 恰好落在双曲线上,此时 A,B,C, D
的对应点分别为 A′,B′,C′,D′,且 C′D′与双曲线交于点 E,求线段
AA′的长及点 E 的坐标.
【答案】(2)如图所示,∵B(6,0),
∴把 x=6 代入反比例解析式得:y=2,即 B′(6,2).
∴平行四边形 ABCD 向上平移 2 个单位,即 AA′=2.
∴D′(0,5).
把 y=5 代入反比例解析式得: ,即
三、解答题
11.如图所示,已知反比例函数 的图象与一次函数 y2=ax+b 的图象交
于点 A(1,4)和点 B(m,-2).
(1)求这两个函数的表达式;
【答案】(1)∵函数 的图象过点 A(1,4),
即 ,∴k=4,即 .
又∵点 B(m,-2)在 上,
∴m=-2,∴B(-2,-2).
又∵一次函数 y2=ax+b 过 A,B 两点,
即 解得 ∴y2=2x+2.
综上可得 y1= 4x ,y2=2x+2. 三、解答题
11.如图所示,已知反比例函数 的图象与一次函数 y2=ax+b 的图象交
于点 A(1,4)和点 B(m,-2).
(2)观察图象,当 x>0 时,直接写出 y1>y2 时自变量 x 的取值范围;
(3)如果点 C 与点 A 关于 x 轴对称,求△ABC 的面积.
【答案】 (2)要使 y1>y2,即函数 y1 的图象总在函数 y2的图象上方,
∴x<-2 或 0<x<1.
(3)如图所示,过点 B 作 BD⊥AC 于点 D,
由图形及题意可得:AC=8,BD=3.
∴△ABC 的面积 谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
