1.2.2 组合 课件(24张PPT)
文档属性
| 名称 | 1.2.2 组合 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 812.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:40:16 | ||
图片预览







文档简介
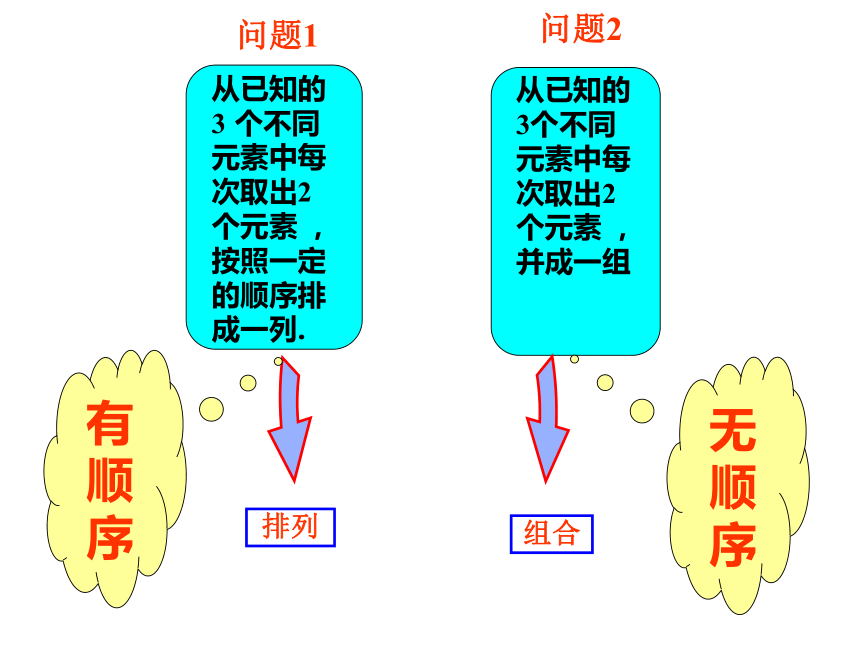
课件24张PPT。1.2.2 组合问题一:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?甲、乙;甲、丙;乙、丙 3情境创设有
顺
序无
顺
序组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.共同点: 都要“从n个不同元素中任取m个元素” 不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.概念讲解组合和排列有什么共同和不同点?判断下列问题是组合问题还是排列问题? (1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个?(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票? 有多少种不同的火车票价?组合问题排列问题(3)10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法?组合问题(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次?组合问题(5)从4个风景点中选出2个游览,有多少种不同的方法?组合问题(6)从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法?排列问题组合问题组合是选择的结果,排列
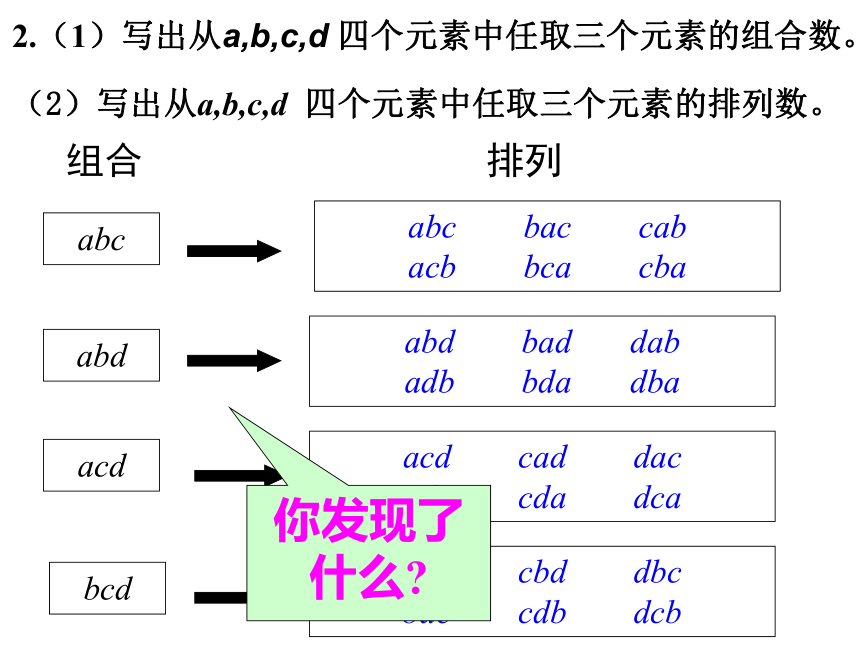
是选择后再排序的结果.概念讲解组合数:我们从具体问题分析:问题一:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?甲、乙;甲、丙;乙、丙 3情境创设组合排列abc bac cab
acb bca cbaabd bad dab
adb bda dbaacd cad dac
adc cda dcabcd cbd dbc
bdc cdb dcb你发现了什么?2.(1)写出从a,b,c,d 四个元素中任取三个元素的组合数。
(2)写出从a,b,c,d 四个元素中任取三个元素的排列数。根据分步计数原理,得到:因此: 组合数公式: 从 n 个不同元中取出m个元素的排列数 概念讲解例1:例2:(1)平面内有10个点,以其中每2个点为端点的线段共有多少条?
(2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?问题2.一个口袋内装有7个不同的白球和1个红球.
(1)从口袋内取出5个球,共有多少种取法?
(2)从口袋内取出5个球,其中恰有1个红球,共有多少种取法?
(3)从口袋内取出5个球,没有红球,共有多少种不同的取法?组合数的两个性质性质1性质2规定:注:
1? 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2? 此性质的作用:恒等变形,简化运算.性质应用1、计算2、解方程1.方程 的解集为( )
练习 1.计算:例3.某次足球赛共12支球队参加,分三个阶段进行:(1)小组赛:经抽签分成甲,乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负。
问全部赛程共需比赛多少场?一、等分组与不等分组问题例:6本不同的书,按下列条件,各有多少种不同的分法;
(1)分给甲、乙、丙三人,每人两本;
(2)分成三份,每份两本;
(3)分成三份,一份1本,一份2本,一份3本;
(4)分给甲、乙、丙3人,一人1本,一人2本,一人3本;方法与技巧练习:
(1)今有10件不同奖品,从中选6件分成三份, 二份各1件,另一份4件, 有多少种分法?
(2) 今有10件不同奖品,从中选6件分给甲乙丙三人,每人二件有多少种分法?解: (1)(2)课堂练习:1、从6位同学中选出4位参加一个座谈会,要求张、王两人中至多有一个人参加,则有不同的选法种数为 。9CD4、把6个学生分到一个工厂的三个车间实习,每个车间2人,若甲必须分到一车间,乙和丙不能分到二车间,则不同的分法有 9 种 。5、某学习小组有5个男生3个女生,从中选3名男生和1名女生参加三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法______种.6、 3 名医生和 6 名护士被分配到 3 所学校为学生体检,每校分配 1 名医生和 2 名护士,不同的分配方法共有多少种?课堂小结1、掌握组合定义,并会求组合数。
2、掌握组合性质并能灵活应用。
3、利用组合知识解决实际问题。布置作业教材22页:A组第六题和B组第1、2题
选做题: 从6个学校中选出30名学生参加数学竞赛,每校至少有1人,这样有几种选法?
分析:问题相当于把30个相同球放入6个不同盒子(盒子不能空的)有几种放法?这类问可用“隔板法”处理.
解:采用“隔板法” 得:
顺
序无
顺
序组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.共同点: 都要“从n个不同元素中任取m个元素” 不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.概念讲解组合和排列有什么共同和不同点?判断下列问题是组合问题还是排列问题? (1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个?(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票? 有多少种不同的火车票价?组合问题排列问题(3)10名同学分成人数相同的数学和英语两个学习小组,共有多少种分法?组合问题(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次?组合问题(5)从4个风景点中选出2个游览,有多少种不同的方法?组合问题(6)从4个风景点中选出2个,并确定这2个风景点的游览顺序,有多少种不同的方法?排列问题组合问题组合是选择的结果,排列
是选择后再排序的结果.概念讲解组合数:我们从具体问题分析:问题一:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?甲、乙;甲、丙;乙、丙 3情境创设组合排列abc bac cab
acb bca cbaabd bad dab
adb bda dbaacd cad dac
adc cda dcabcd cbd dbc
bdc cdb dcb你发现了什么?2.(1)写出从a,b,c,d 四个元素中任取三个元素的组合数。
(2)写出从a,b,c,d 四个元素中任取三个元素的排列数。根据分步计数原理,得到:因此: 组合数公式: 从 n 个不同元中取出m个元素的排列数 概念讲解例1:例2:(1)平面内有10个点,以其中每2个点为端点的线段共有多少条?
(2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?问题2.一个口袋内装有7个不同的白球和1个红球.
(1)从口袋内取出5个球,共有多少种取法?
(2)从口袋内取出5个球,其中恰有1个红球,共有多少种取法?
(3)从口袋内取出5个球,没有红球,共有多少种不同的取法?组合数的两个性质性质1性质2规定:注:
1? 公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与原组合数上标较大的相同的一个组合数.
2? 此性质的作用:恒等变形,简化运算.性质应用1、计算2、解方程1.方程 的解集为( )
练习 1.计算:例3.某次足球赛共12支球队参加,分三个阶段进行:(1)小组赛:经抽签分成甲,乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负。
问全部赛程共需比赛多少场?一、等分组与不等分组问题例:6本不同的书,按下列条件,各有多少种不同的分法;
(1)分给甲、乙、丙三人,每人两本;
(2)分成三份,每份两本;
(3)分成三份,一份1本,一份2本,一份3本;
(4)分给甲、乙、丙3人,一人1本,一人2本,一人3本;方法与技巧练习:
(1)今有10件不同奖品,从中选6件分成三份, 二份各1件,另一份4件, 有多少种分法?
(2) 今有10件不同奖品,从中选6件分给甲乙丙三人,每人二件有多少种分法?解: (1)(2)课堂练习:1、从6位同学中选出4位参加一个座谈会,要求张、王两人中至多有一个人参加,则有不同的选法种数为 。9CD4、把6个学生分到一个工厂的三个车间实习,每个车间2人,若甲必须分到一车间,乙和丙不能分到二车间,则不同的分法有 9 种 。5、某学习小组有5个男生3个女生,从中选3名男生和1名女生参加三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法______种.6、 3 名医生和 6 名护士被分配到 3 所学校为学生体检,每校分配 1 名医生和 2 名护士,不同的分配方法共有多少种?课堂小结1、掌握组合定义,并会求组合数。
2、掌握组合性质并能灵活应用。
3、利用组合知识解决实际问题。布置作业教材22页:A组第六题和B组第1、2题
选做题: 从6个学校中选出30名学生参加数学竞赛,每校至少有1人,这样有几种选法?
分析:问题相当于把30个相同球放入6个不同盒子(盒子不能空的)有几种放法?这类问可用“隔板法”处理.
解:采用“隔板法” 得:
