1.3.2 杨辉三角 课件(24张PPT)
文档属性
| 名称 | 1.3.2 杨辉三角 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 877.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:44:20 | ||
图片预览





文档简介
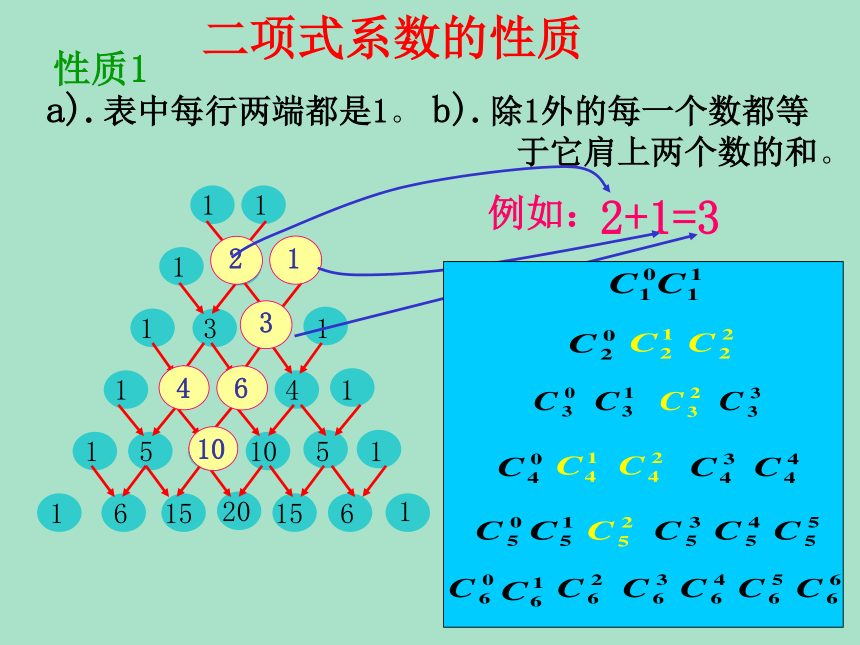
课件24张PPT。1.3.2杨辉三角复习回顾:二项式系数通 项一般地,对于n N*有二项式定理:我们先通过观察n为特殊值时,二项式系数有什么特点?1.“杨辉三角”的来历及规律 杨辉三角1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 …… …… ……a).表中每行两端都是1。b).除1外的每一个数都等
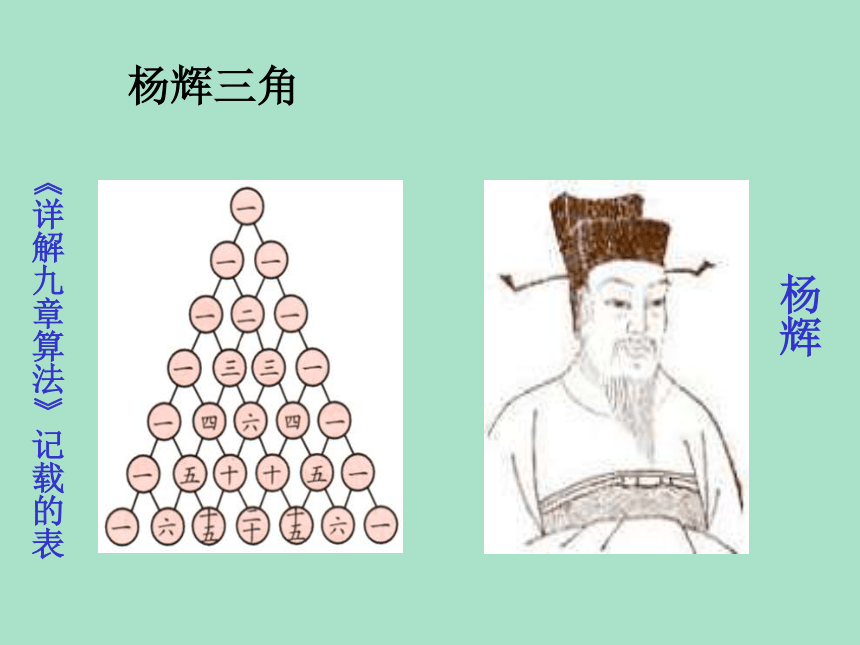
于它肩上两个数的和。4+6=10二项式系数的性质性质1《详解九章算法》记载的表
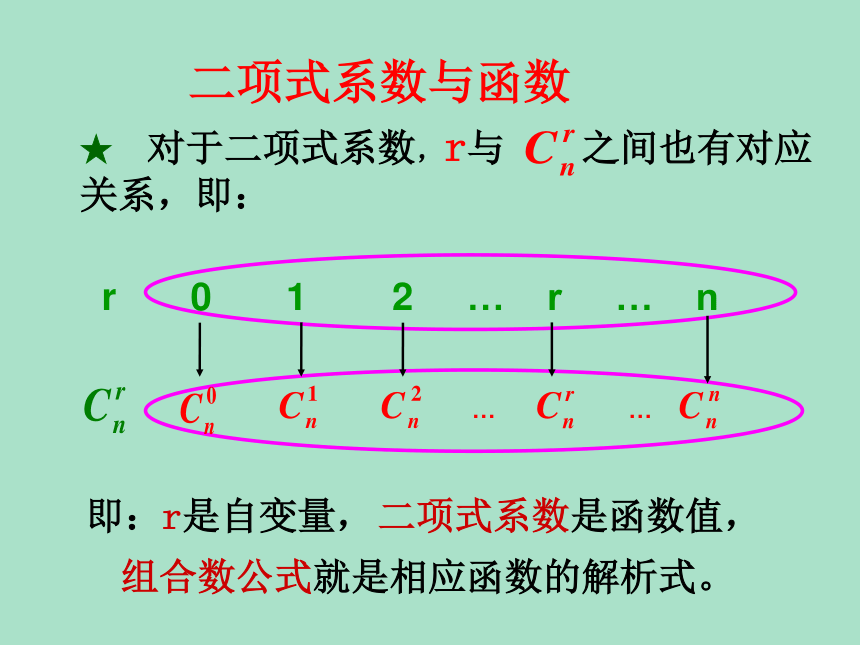
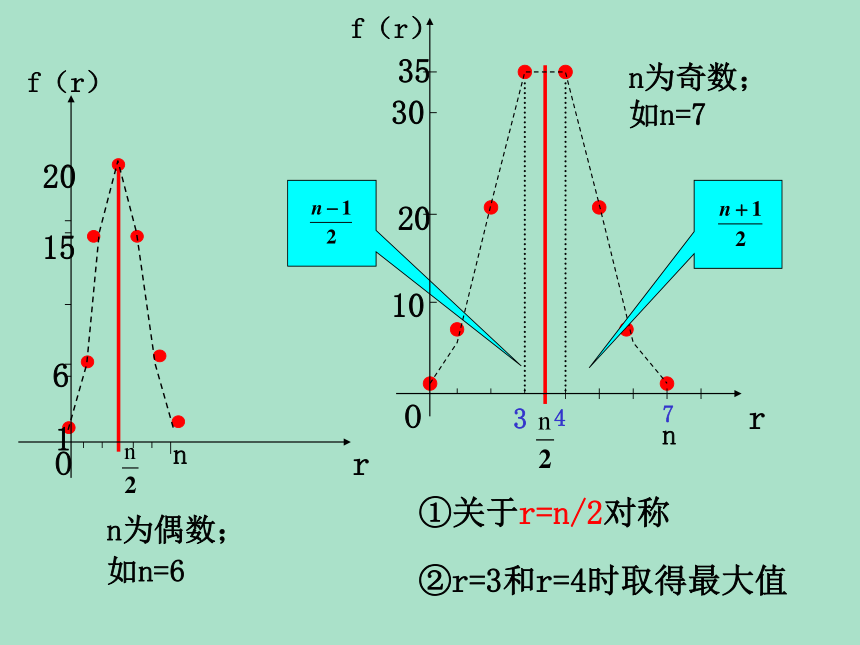
杨辉三角杨辉二项式系数的性质对称二项式系数与函数 即:r是自变量,二项式系数是函数值,组合数公式就是相应函数的解析式。……f(r)n为奇数;
如n=7n为偶数;
如n=6①关于r=n/2对称②r=3和r=4时取得最大值r(3)增减性与最大值. 二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。
当n是奇数时,中间两项的二项式系数 ,
相等,且同时取得最大值。 二项式系数的性质 与首末两端“等距离”的两个二项式系数相等性质2:对称性性质3:增减性与最大值先增后减211111111334465510101行2行3行4行5行n行11=+=+++++=++++=+++=++2122232425···· · ·二项式系数和例1. 证明在 的展开式中,奇数项的二项式系数和等于偶数项的二项式系数和.=?赋值法再应用(4)各二项式系数的和 奇数项的二项式系数和等于偶数项的二项式系数和,即1.二项式系数的四个性质:①递推性: Cn0= Cnn=1
Cn+1m= Cnm + Cnm-1
② 对称性:Cnm= Cnn-m③二项式系数的单调性与最大值: n 偶数,最中间一项的二项式系数最大,即 n 奇数,最中间两项的二项式系数相等且最大,即 ,④二项式系数和:奇数项的二项式系数和等于偶数项的二项式系数和,即课堂练习:
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;a+b19(4)求(1-2x)7展开式中系数最大的项和系数最小的项.解:展开式中系数正负相间,研究系数绝对值由可知r从0到5 ,系数的绝对值增大,r从5到7 ,系数的绝对值减小.故当r=5时,系数最小项为当r=4或6时,二者中系数较大者为系数最大项得当r=4时,系数最大项为赋值法的应用
—解决二项式系数问题.赋值法例2再结合(2)(3)得,其值为2187 1.利用杨辉三角和函数图象可得二项式 系数的对称性、增减性和最大值;
2.注意二项式系数与系数的区别;
3.常用赋值法解决二项式系数问题.如果把此题改为:
在(1+2x)4的展开式中,系数最大的项是?
试归纳出求形如( ax + b) n 展开式中系数最大项的方法或步骤。在(1+x)4的展开式中,二项式系数最大的项是?
去掉“二项式”三个字解法是否一样?2.课后探究:1.课本30页 练习A
31页 练习B作业谢谢指导,再见!
于它肩上两个数的和。4+6=10二项式系数的性质性质1《详解九章算法》记载的表
杨辉三角杨辉二项式系数的性质对称二项式系数与函数 即:r是自变量,二项式系数是函数值,组合数公式就是相应函数的解析式。……f(r)n为奇数;
如n=7n为偶数;
如n=6①关于r=n/2对称②r=3和r=4时取得最大值r(3)增减性与最大值. 二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。
当n是奇数时,中间两项的二项式系数 ,
相等,且同时取得最大值。 二项式系数的性质 与首末两端“等距离”的两个二项式系数相等性质2:对称性性质3:增减性与最大值先增后减211111111334465510101行2行3行4行5行n行11=+=+++++=++++=+++=++2122232425···· · ·二项式系数和例1. 证明在 的展开式中,奇数项的二项式系数和等于偶数项的二项式系数和.=?赋值法再应用(4)各二项式系数的和 奇数项的二项式系数和等于偶数项的二项式系数和,即1.二项式系数的四个性质:①递推性: Cn0= Cnn=1
Cn+1m= Cnm + Cnm-1
② 对称性:Cnm= Cnn-m③二项式系数的单调性与最大值: n 偶数,最中间一项的二项式系数最大,即 n 奇数,最中间两项的二项式系数相等且最大,即 ,④二项式系数和:奇数项的二项式系数和等于偶数项的二项式系数和,即课堂练习:
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;a+b19(4)求(1-2x)7展开式中系数最大的项和系数最小的项.解:展开式中系数正负相间,研究系数绝对值由可知r从0到5 ,系数的绝对值增大,r从5到7 ,系数的绝对值减小.故当r=5时,系数最小项为当r=4或6时,二者中系数较大者为系数最大项得当r=4时,系数最大项为赋值法的应用
—解决二项式系数问题.赋值法例2再结合(2)(3)得,其值为2187 1.利用杨辉三角和函数图象可得二项式 系数的对称性、增减性和最大值;
2.注意二项式系数与系数的区别;
3.常用赋值法解决二项式系数问题.如果把此题改为:
在(1+2x)4的展开式中,系数最大的项是?
试归纳出求形如( ax + b) n 展开式中系数最大项的方法或步骤。在(1+x)4的展开式中,二项式系数最大的项是?
去掉“二项式”三个字解法是否一样?2.课后探究:1.课本30页 练习A
31页 练习B作业谢谢指导,再见!
