1.3.2 杨辉三角 课件(22张PPT)
文档属性
| 名称 | 1.3.2 杨辉三角 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:43:19 | ||
图片预览






文档简介
课件22张PPT。
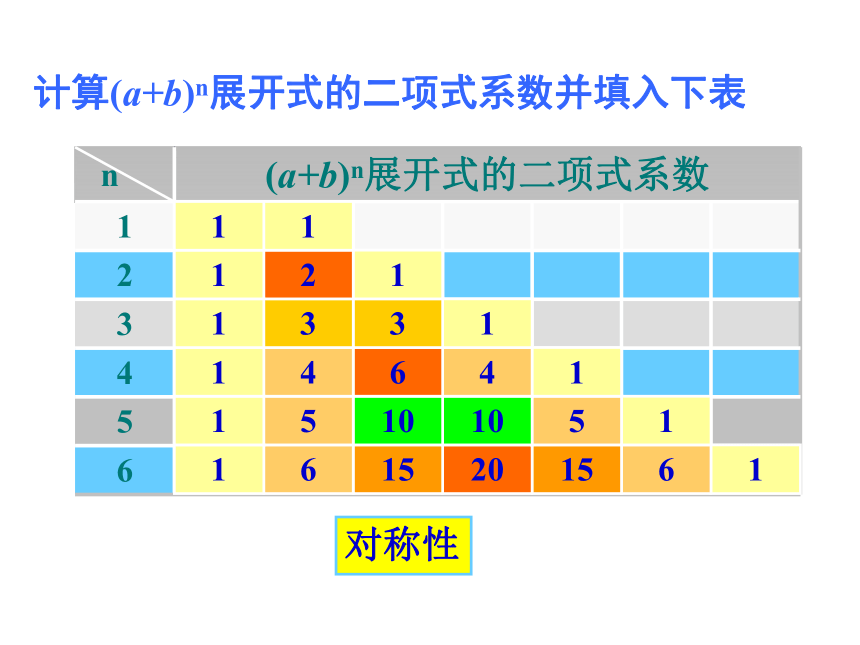
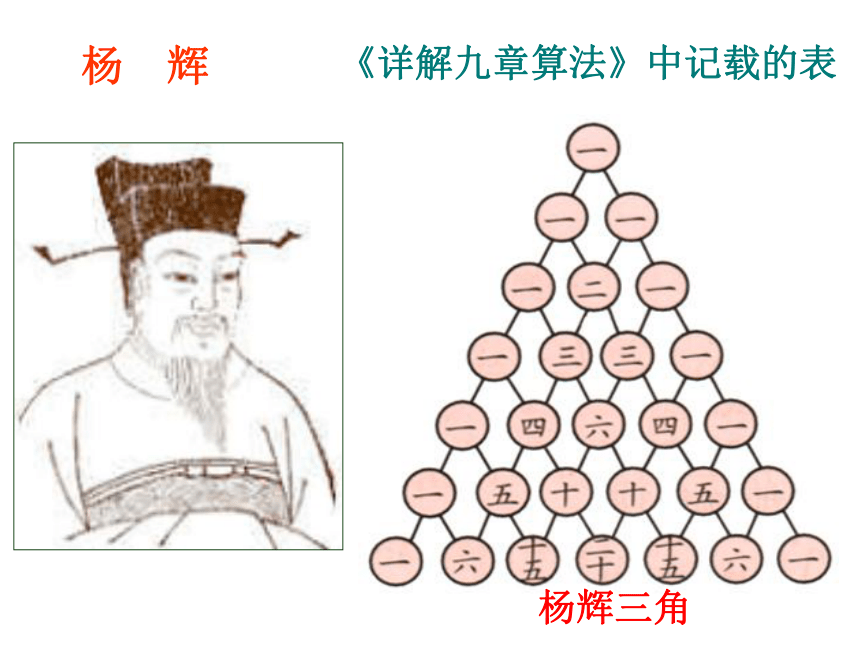
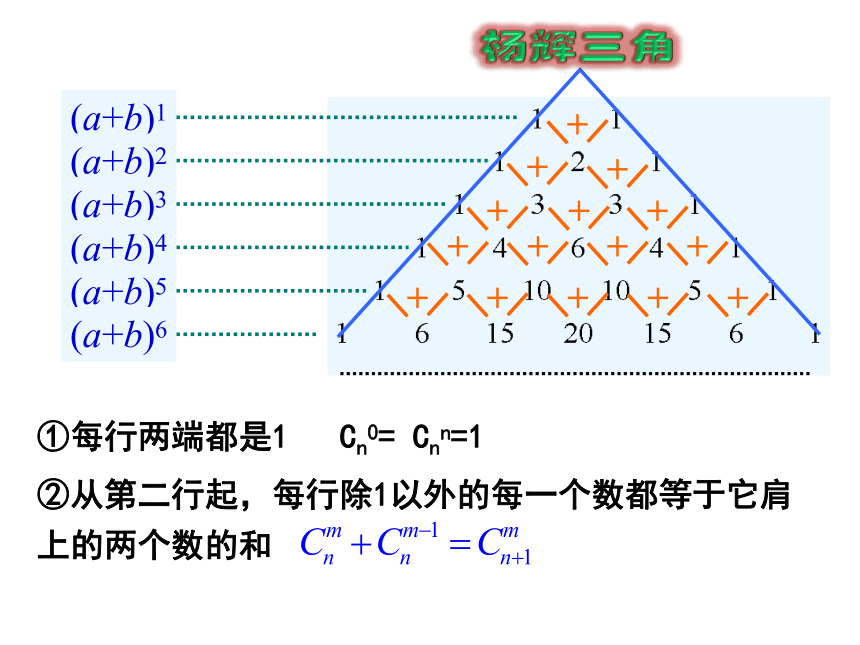
1.3.2 杨辉三角二项展开式中的二项式系数指的是哪些?共有多少个?45 下面我们来研究二项式系数有些什么性质?我们先通过观察n为特殊值时,二项式系数有什么特点?计算(a+b)n展开式的二项式系数并填入下表对称性《详解九章算法》中记载的表杨 辉杨辉三角①每行两端都是1 Cn0= Cnn=1
②从第二行起,每行除1以外的每一个数都等于它肩上的两个数的和 展开式的二项式系数依次是: 从函数角度看, 可看成是以r为自变量的函数 ,其定义域是: 当 时,其图象是右图中的7个孤立点.(2)对称性 与首末两端“等距离”的两个二项式系数相等.这一性质可直接由公式
得到.图象的对称轴:(3)增减性与最大值 由于:所以 相对于 的增减情况由 决定. 由: 可知,当 时,二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 (3)增减性与最大值 (4)各二项式系数的和 在二项式定理中,令 ,则: 这就是说,
的展开式的各二项式系数的和等于: (1) 一般地, 展开式的二项式系数
有如下基本性质: (2)(4)(对称性)第0行 1第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 1第5行 1 5 1第6行 1 6 15 6 1第n-1行 11 第n行 11…… ……… ……………… … … 第7行 1 7 21 21 7 11035++++=3551520104“斜线和”= 125第5行 1 5 10 10 5 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第1行 1 1第0行 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1……138132134如图,写出斜线上各行数字的和,有什么规律?第8行 1 8 28 56 70 56 28 8 1 从第三个数起,任一数都等于前两个数的和,
这就是著名的斐波那契数列 ,也称为兔子数列。例1 证明:在(a+b)n展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。在二项式定理中,令 ,则: 已知
求:(1) ;
(2) ;
(3) ;
(4)例2 已知 展开式的各项二项式系数和等于1024,求展开式中含 的项.类型:求展开式中二项式系数和类型:求展开式中二项式系数、系数的最大的项方法:利用通项公式建立不等式组例3求 的展开式中二项式系数最大的项.变式1:求 的展开式中系数最大的项.变式2:求 的展开式中系数最大 的项.变式练习:
在(3x -2y)20的展开式中,求:
(1)二项式系数最大的项;(2)系数绝对值最大的项.解:(2)设系数绝对值最大的项是第r+1项.则(1)二项式系数的四个性质 (2) 数学思想:函数思想 a 单调性; b 图象;c 最值.小 结 2.求证:
1.3.2 杨辉三角二项展开式中的二项式系数指的是哪些?共有多少个?45 下面我们来研究二项式系数有些什么性质?我们先通过观察n为特殊值时,二项式系数有什么特点?计算(a+b)n展开式的二项式系数并填入下表对称性《详解九章算法》中记载的表杨 辉杨辉三角①每行两端都是1 Cn0= Cnn=1
②从第二行起,每行除1以外的每一个数都等于它肩上的两个数的和 展开式的二项式系数依次是: 从函数角度看, 可看成是以r为自变量的函数 ,其定义域是: 当 时,其图象是右图中的7个孤立点.(2)对称性 与首末两端“等距离”的两个二项式系数相等.这一性质可直接由公式
得到.图象的对称轴:(3)增减性与最大值 由于:所以 相对于 的增减情况由 决定. 由: 可知,当 时,二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 (3)增减性与最大值 (4)各二项式系数的和 在二项式定理中,令 ,则: 这就是说,
的展开式的各二项式系数的和等于: (1) 一般地, 展开式的二项式系数
有如下基本性质: (2)(4)(对称性)第0行 1第1行 1 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 1第5行 1 5 1第6行 1 6 15 6 1第n-1行 11 第n行 11…… ……… ……………… … … 第7行 1 7 21 21 7 11035++++=3551520104“斜线和”= 125第5行 1 5 10 10 5 1第6行 1 6 15 20 15 6 1第7行 1 7 21 35 35 21 7 1第1行 1 1第0行 1第2行 1 2 1第3行 1 3 3 1第4行 1 4 6 4 1……138132134如图,写出斜线上各行数字的和,有什么规律?第8行 1 8 28 56 70 56 28 8 1 从第三个数起,任一数都等于前两个数的和,
这就是著名的斐波那契数列 ,也称为兔子数列。例1 证明:在(a+b)n展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。在二项式定理中,令 ,则: 已知
求:(1) ;
(2) ;
(3) ;
(4)例2 已知 展开式的各项二项式系数和等于1024,求展开式中含 的项.类型:求展开式中二项式系数和类型:求展开式中二项式系数、系数的最大的项方法:利用通项公式建立不等式组例3求 的展开式中二项式系数最大的项.变式1:求 的展开式中系数最大的项.变式2:求 的展开式中系数最大 的项.变式练习:
在(3x -2y)20的展开式中,求:
(1)二项式系数最大的项;(2)系数绝对值最大的项.解:(2)设系数绝对值最大的项是第r+1项.则(1)二项式系数的四个性质 (2) 数学思想:函数思想 a 单调性; b 图象;c 最值.小 结 2.求证:
