2.1.2 离散型随机变量的分布列 课件(20张PPT)
文档属性
| 名称 | 2.1.2 离散型随机变量的分布列 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:45:09 | ||
图片预览







文档简介
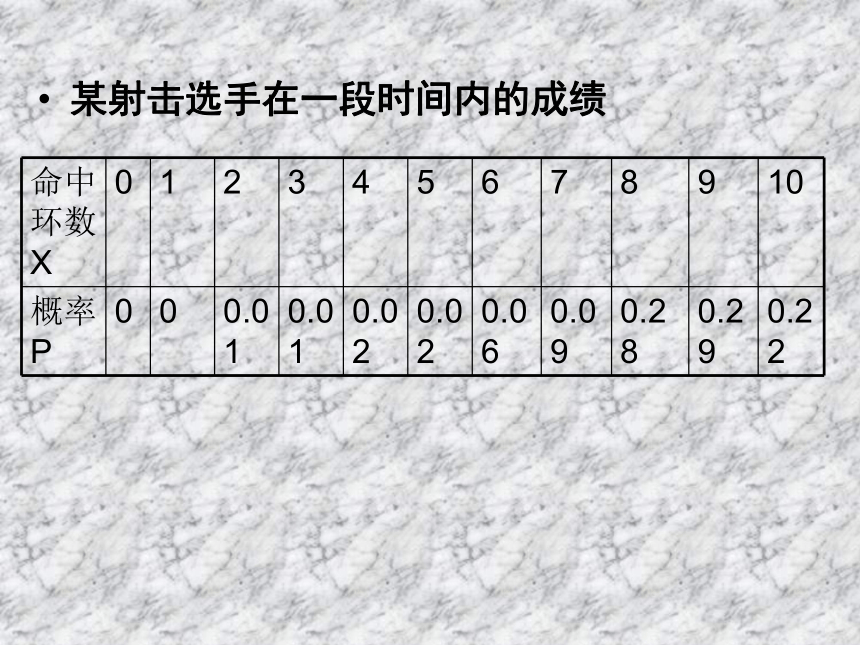
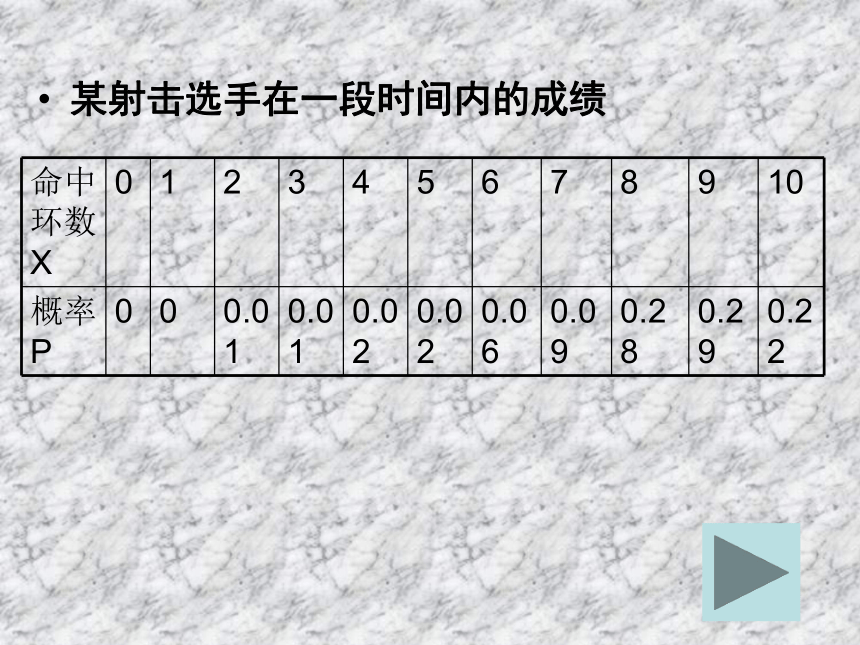
课件20张PPT。2.1.2离散型随机变量的分布列人教B版《数学选修2-3 》复习回顾: 如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量。随机变量常用大写字母X,Y等表示。 如果随机变量X的所有可能取值都能一一列出,则X叫做离散型随机变量 。随机变量:离散型随机变量:某射击选手在一段时间内的成绩提出问题掌握一个离散型随机变量X的取值规律,必须知道1、X所有可能取的值x1,x2,…,xn. 2、X取每一个值xi的概率p1,p2,…,pn.离散型随机变量的分布列一般地,设离散型随机变量X可能取的值为
x1,x2,…,xi,… xn.
X取每一个值xi(i=1,2,…n)的概率pi,则称表为离散型随机变量X的概率分布,简称为X的分布列概念形成求离散型随机变量的分布列的步骤:3、列成表格。1.找出离散型随机变量X可能取的值x1,x2,…,xi,… xn
2.求X的每个概率p1,p2,…,pi,… pn.某射击选手在一段时间内的成绩概念深化注意:随机变量X在一个范围的概率等于此范围内的 所有取值的概率总和。离散型随机变量的分布列的性质:1、 pi≥0, i=1,2,…n。2、 p1+p2+…+ pn=1. 例1 篮球运动员在比赛中每次罚球命中得1分,不中得0分。已知某运动员罚球命中的概率是0.7,求他罚球一次的得分的分布列。应用举例 2、投掷一枚硬币,设X=1表示出现正面,X=0表示出现反面,求离散型随机变量X的分布列。对应练习:教材第44页A2 对应练习:教材第44页B2 2、某商店购进一批西瓜,预计晴天西瓜畅销,可获利1000元;阴天销路一般,可获利500元;下雨天西瓜滞销,这时将亏损500元。根据天气预报,未来数日晴天的概率为0.4,阴天的概率为0.2,下雨的概率为0.4,试写出销售这批西瓜获利的分布列。应用举例 例2.抛掷一枚骰子,所得的点数为X:
(1) 求X的分布列;
(2)求点数大于四的概率;
(3)求点数不超过5的概率。对应练习:教材第44页A4 4.抛掷两枚骰子,所得的点数之和为X:
(1) 求X的分布列;
(2)求点数之和大于9的概率;
(3)求点数之和不超过7的概率。课堂练习:1、设随机变量 的分布列如下:则 的值为 .2、设随机变量 的分布列为则 的值为 .27/13 3、X的分布列为求常数a。解:由离散型随机变量的分布列的性质有课堂小结:本节学习的主要内容及学习目标要求:1、理解离散型随机变量的分布列的意义,会求某些简单的离散型随机变量的分布列;
2、掌握离散型随机变量的分布列的基本
性质,并会用它们来解决一些简单问题.
课后作业
必做题:练习册第21页—22页。
选做题:练习册第23页—24页。谢谢合作,再见!
x1,x2,…,xi,… xn.
X取每一个值xi(i=1,2,…n)的概率pi,则称表为离散型随机变量X的概率分布,简称为X的分布列概念形成求离散型随机变量的分布列的步骤:3、列成表格。1.找出离散型随机变量X可能取的值x1,x2,…,xi,… xn
2.求X的每个概率p1,p2,…,pi,… pn.某射击选手在一段时间内的成绩概念深化注意:随机变量X在一个范围的概率等于此范围内的 所有取值的概率总和。离散型随机变量的分布列的性质:1、 pi≥0, i=1,2,…n。2、 p1+p2+…+ pn=1. 例1 篮球运动员在比赛中每次罚球命中得1分,不中得0分。已知某运动员罚球命中的概率是0.7,求他罚球一次的得分的分布列。应用举例 2、投掷一枚硬币,设X=1表示出现正面,X=0表示出现反面,求离散型随机变量X的分布列。对应练习:教材第44页A2 对应练习:教材第44页B2 2、某商店购进一批西瓜,预计晴天西瓜畅销,可获利1000元;阴天销路一般,可获利500元;下雨天西瓜滞销,这时将亏损500元。根据天气预报,未来数日晴天的概率为0.4,阴天的概率为0.2,下雨的概率为0.4,试写出销售这批西瓜获利的分布列。应用举例 例2.抛掷一枚骰子,所得的点数为X:
(1) 求X的分布列;
(2)求点数大于四的概率;
(3)求点数不超过5的概率。对应练习:教材第44页A4 4.抛掷两枚骰子,所得的点数之和为X:
(1) 求X的分布列;
(2)求点数之和大于9的概率;
(3)求点数之和不超过7的概率。课堂练习:1、设随机变量 的分布列如下:则 的值为 .2、设随机变量 的分布列为则 的值为 .27/13 3、X的分布列为求常数a。解:由离散型随机变量的分布列的性质有课堂小结:本节学习的主要内容及学习目标要求:1、理解离散型随机变量的分布列的意义,会求某些简单的离散型随机变量的分布列;
2、掌握离散型随机变量的分布列的基本
性质,并会用它们来解决一些简单问题.
课后作业
必做题:练习册第21页—22页。
选做题:练习册第23页—24页。谢谢合作,再见!
