2.1.2 离散型随机变量的分布列 课件(21张PPT)
文档属性
| 名称 | 2.1.2 离散型随机变量的分布列 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:45:49 | ||
图片预览








文档简介
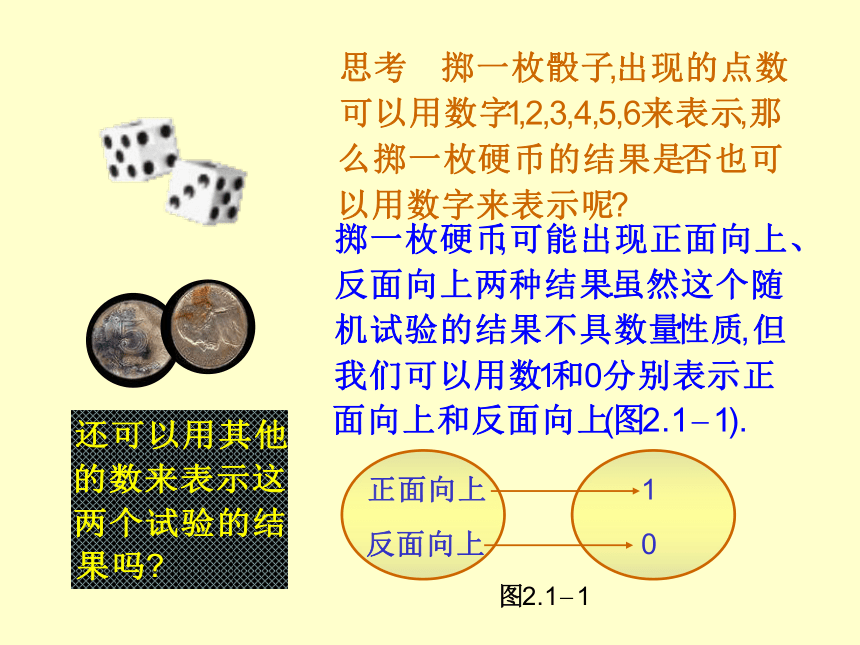
课件21张PPT。例1.某一射手射击所得的环数ξ的分布列如下:求此射手“射击一次命中环数≥7”的概率 解:根据射手射击所得的环数ξ的分布列,有
P(ξ=7)=0.09, P(ξ=8)=0.28,
P(ξ=9)=0.29, P(ξ=10)=0.22.
所求的概率为
P(ξ≥7)=0.09+0.28+0.29+0.22=0.883.两点分布列:
例2.在掷一枚图钉的随机试验中,令
如果针尖向上的概率为试写出随机变量 X 的分布列. 解:根据分布列的性质,针尖向下的概率是于是,随机变量 X 的分布列是像上面这样的分布列称为两点分布列. 两点分布又称0一1分布.由于只有两个可能结果的
随机试验叫伯努利( Bernoulli ) 试验,所以还称这种
分布为伯努利分布.
4. 超几何分布列:例3.在含有 5 件次品的 100 件产品中,任取 3 件,试求:
(1)取到的次品数X 的分布列;
(2)至少取到1件次品的概率解: (1)由于从 100 件产品中任取3 件的结果数为,从100 件产品中任取3件,其中恰有k 件次品的结果数为那么从 100 件产品中任取 3 件,其中恰有 k 件次品的概率为所以随机变量 X 的分布列是(2)根据随机变量X 的分布列,可得至少取到 1 件次品的概率
P ( X≥1 ) = P ( X = 1 ) + P ( X = 2 ) + P ( X = 3 ) ≈0.138 06 + 0. 005 88 + 0. 00006 = 0. 144 00 .一般地,在含有M 件次品的 N 件产品中,任取 n 件,
其中恰有X件次品数,则事件 {X=k}发生的概率为其中,且称分布列为超几何分布列.如果随机变量 X 的分布列为超几何分布列,则称随机变量 X 服从超几何分布随堂练习:中装有10个红球和20个白球,这些球除颜色外完全相同.
一次从中摸出5个球,至少摸到3个红球就中奖.
求中奖的概率.解:设摸出红球的个数为X,则X服从超几何分布,
其中 N = 30 , M=10, n=5 .于是中奖的概率 P (X≥3 ) = P (X =3 ) + P ( X = 4 )十 P ( X = 5 )
=≈0.191. 在某年级的联欢会上设计了一个摸奖游戏,在一个口袋注:求离散型随机变量的概率分布的步骤:(1)确定随机变量的所有可能的值xi(2)求出各取值的概率p(=xi)=pi(3)画出表格五、小结 : (3)离散型随机变量的超几何分布(1)根据随机变量的概率分步(分步列),可以求随机事件的概率;(2)两点分布是一种常见的离散型随机变量的分布,它是概率论中最重要的几种分布之一 六、课后作业:作业10
P(ξ=7)=0.09, P(ξ=8)=0.28,
P(ξ=9)=0.29, P(ξ=10)=0.22.
所求的概率为
P(ξ≥7)=0.09+0.28+0.29+0.22=0.883.两点分布列:
例2.在掷一枚图钉的随机试验中,令
如果针尖向上的概率为试写出随机变量 X 的分布列. 解:根据分布列的性质,针尖向下的概率是于是,随机变量 X 的分布列是像上面这样的分布列称为两点分布列. 两点分布又称0一1分布.由于只有两个可能结果的
随机试验叫伯努利( Bernoulli ) 试验,所以还称这种
分布为伯努利分布.
4. 超几何分布列:例3.在含有 5 件次品的 100 件产品中,任取 3 件,试求:
(1)取到的次品数X 的分布列;
(2)至少取到1件次品的概率解: (1)由于从 100 件产品中任取3 件的结果数为,从100 件产品中任取3件,其中恰有k 件次品的结果数为那么从 100 件产品中任取 3 件,其中恰有 k 件次品的概率为所以随机变量 X 的分布列是(2)根据随机变量X 的分布列,可得至少取到 1 件次品的概率
P ( X≥1 ) = P ( X = 1 ) + P ( X = 2 ) + P ( X = 3 ) ≈0.138 06 + 0. 005 88 + 0. 00006 = 0. 144 00 .一般地,在含有M 件次品的 N 件产品中,任取 n 件,
其中恰有X件次品数,则事件 {X=k}发生的概率为其中,且称分布列为超几何分布列.如果随机变量 X 的分布列为超几何分布列,则称随机变量 X 服从超几何分布随堂练习:中装有10个红球和20个白球,这些球除颜色外完全相同.
一次从中摸出5个球,至少摸到3个红球就中奖.
求中奖的概率.解:设摸出红球的个数为X,则X服从超几何分布,
其中 N = 30 , M=10, n=5 .于是中奖的概率 P (X≥3 ) = P (X =3 ) + P ( X = 4 )十 P ( X = 5 )
=≈0.191. 在某年级的联欢会上设计了一个摸奖游戏,在一个口袋注:求离散型随机变量的概率分布的步骤:(1)确定随机变量的所有可能的值xi(2)求出各取值的概率p(=xi)=pi(3)画出表格五、小结 : (3)离散型随机变量的超几何分布(1)根据随机变量的概率分步(分步列),可以求随机事件的概率;(2)两点分布是一种常见的离散型随机变量的分布,它是概率论中最重要的几种分布之一 六、课后作业:作业10
