2.1.3 超几何分布 课件(27张PPT)
文档属性
| 名称 | 2.1.3 超几何分布 课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览




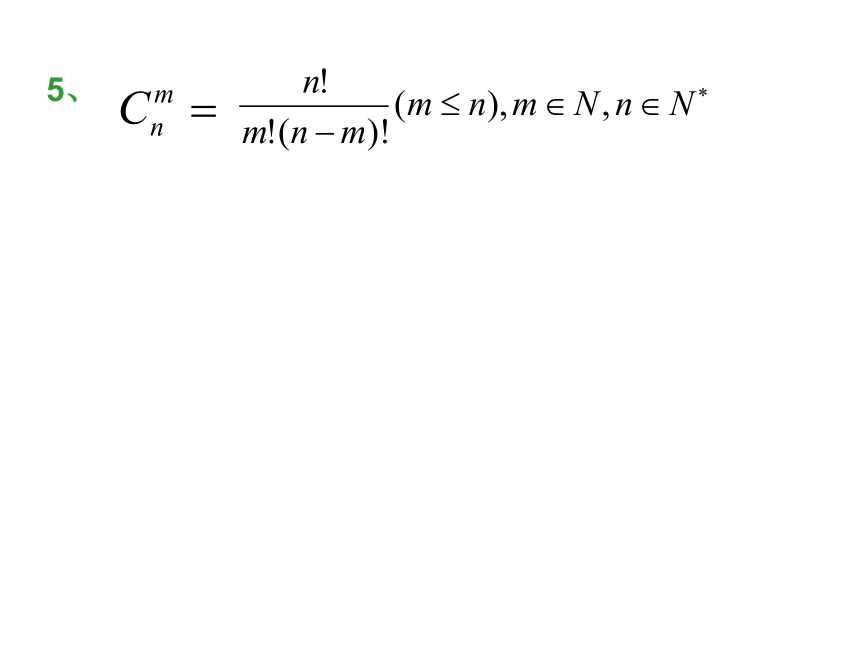



文档简介
课件27张PPT。2.1.3超几何分布一、复习引入:2、离散型随机变量所有取值可以一一列出的随机变量,称为离散型随机变量。如果试验的结果可以用一个变量X来表示,并且X是随着试验结果的不同而变化的,那么这样的变量X叫做随机变量.常用字母X,Y,…,等表示1、随机变量①试验包含有限个不同的基本事件;
②每个基本事件发生的可能性相等。3、古典概型:4、离散型随机变量的分布列:一般地,若离散型随机变量X 可能取的不同值为:
x1,x2,…,xi,…,xn,X取每一个值xi (i=1,2,…,n)的概P(X=xi)=Pi,则称表:为离散型随机变量X的概率分布,简称为X的分布列.分布列具有性质:5、从含有6男4女的10名同学中随机抽取3名同学去采集标本,抽到的女生数为X.
问题1:这10人可分几类?
两类:男生和女生
问题2:取到女生数X的取值有哪些?
X的取值:0、1、2、3.
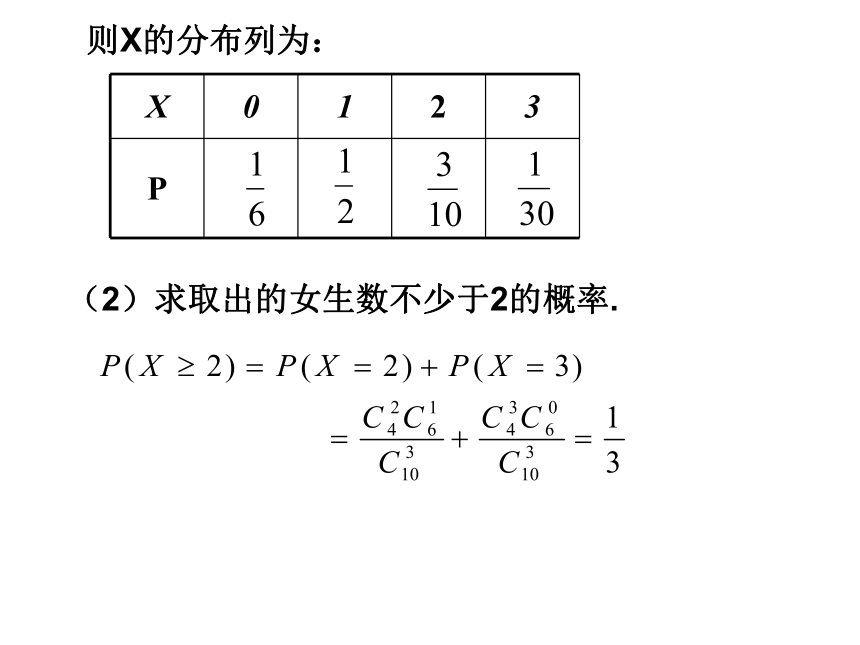
问题3:求女生数X=2的概率.二、新课讲授:一般地,设有总数为N件的两类物品,其中一类有M件,从所有物品中任取n件( ),这n件中所含这类物品件数X是一个离散型随机变量,它取值为m时的概率为我们称离散型随机变量X的这种形式的概率分布为超几何分布,也称X服从参数为N,M,n的超几何分布.超几何分布:例1:从含有6男4女的10名同学中随机抽取3名同学去采集标本,(1)求取到女生数X的分布列;解:X服从参数为N=10,M=4,n=3的超几何分布,它的可能取值为0,1,2,3,根据公式可以算出其相应的概率依次为(2)求取出的女生数不少于2的概率.(2)求取出的女生数不少于2的概率.则X的分布列为:如何解决超几何分布问题:
(1)确定所给问题中的变量服从超几何分布;
(2)写出超几何分布中的参数N,M,n的值;
(3)利用超几何分布公式,求出相应问题的概率.例2、从一批含有13件正品、2件次品的产品中,任取3件,求取得的次品数X的分布列A小组讨论:2.现有语文、数学课本共7本(其中语文课本不少于2本),从中任取2本,至多有1本语文课本的概率是5/7,则语文课本共有 ( )
A.2本 B.3本 C.4本 D.5本2.现有语文、数学课本共7本(其中语文课本不少于2本),从中任取2本,至多有1本语文课本的概率是5/7,则语文课本共有 ( )
A.2本 B.3本 C.4本 D.5本C例3、现有10张奖券,其中8张1元的、2张5元的,从中任取3张,(1)求所得金额的分布列.(2)求“所得金额X不超过10元”的概率.(2)所得金额X不超过10元的概率为3、如何解决超几何分布问题:
(1)确定所给问题中的变量服从超几何分布;
(2)写出超几何分布中的参数N,M,n的值;
(3)利用超几何分布公式,求出相应问题的概率.小结1、超几何分布的定义2、超几何分布概率计算公式 练习1、在10件产品中,有3件一等品,4件二等品,3件三等品.从这10件产品中任取3件.求:
(1)取出的3件产品中一等品件数X的分布列;
(2)取出的3件产品中一等品件数多于二等品件数的概率.P46 练习 A 、B 教材 例2
习题2—1 A 、B
作业:习题2—1 A 4课后作业补充练习2、袋中装有4个白棋子、3个黑棋子,从袋中随机地取棋
子,设取到一个白棋子得2分,取到一个黑棋子得1分,从袋中任取4个棋子.
(1)求得分X的分布列;
(2)求得分大于6的概率.
解:(1)袋中共7个棋子,以取到白棋子为标准,则取到白棋子的个数为1,2,3,4,对应的得分X为5,6,7,8.
由题意知,取到的白棋子数服从参数为N=7,M=4,n=4的超几何分布,故得分也服从该超几何分布.
②每个基本事件发生的可能性相等。3、古典概型:4、离散型随机变量的分布列:一般地,若离散型随机变量X 可能取的不同值为:
x1,x2,…,xi,…,xn,X取每一个值xi (i=1,2,…,n)的概P(X=xi)=Pi,则称表:为离散型随机变量X的概率分布,简称为X的分布列.分布列具有性质:5、从含有6男4女的10名同学中随机抽取3名同学去采集标本,抽到的女生数为X.
问题1:这10人可分几类?
两类:男生和女生
问题2:取到女生数X的取值有哪些?
X的取值:0、1、2、3.
问题3:求女生数X=2的概率.二、新课讲授:一般地,设有总数为N件的两类物品,其中一类有M件,从所有物品中任取n件( ),这n件中所含这类物品件数X是一个离散型随机变量,它取值为m时的概率为我们称离散型随机变量X的这种形式的概率分布为超几何分布,也称X服从参数为N,M,n的超几何分布.超几何分布:例1:从含有6男4女的10名同学中随机抽取3名同学去采集标本,(1)求取到女生数X的分布列;解:X服从参数为N=10,M=4,n=3的超几何分布,它的可能取值为0,1,2,3,根据公式可以算出其相应的概率依次为(2)求取出的女生数不少于2的概率.(2)求取出的女生数不少于2的概率.则X的分布列为:如何解决超几何分布问题:
(1)确定所给问题中的变量服从超几何分布;
(2)写出超几何分布中的参数N,M,n的值;
(3)利用超几何分布公式,求出相应问题的概率.例2、从一批含有13件正品、2件次品的产品中,任取3件,求取得的次品数X的分布列A小组讨论:2.现有语文、数学课本共7本(其中语文课本不少于2本),从中任取2本,至多有1本语文课本的概率是5/7,则语文课本共有 ( )
A.2本 B.3本 C.4本 D.5本2.现有语文、数学课本共7本(其中语文课本不少于2本),从中任取2本,至多有1本语文课本的概率是5/7,则语文课本共有 ( )
A.2本 B.3本 C.4本 D.5本C例3、现有10张奖券,其中8张1元的、2张5元的,从中任取3张,(1)求所得金额的分布列.(2)求“所得金额X不超过10元”的概率.(2)所得金额X不超过10元的概率为3、如何解决超几何分布问题:
(1)确定所给问题中的变量服从超几何分布;
(2)写出超几何分布中的参数N,M,n的值;
(3)利用超几何分布公式,求出相应问题的概率.小结1、超几何分布的定义2、超几何分布概率计算公式 练习1、在10件产品中,有3件一等品,4件二等品,3件三等品.从这10件产品中任取3件.求:
(1)取出的3件产品中一等品件数X的分布列;
(2)取出的3件产品中一等品件数多于二等品件数的概率.P46 练习 A 、B 教材 例2
习题2—1 A 、B
作业:习题2—1 A 4课后作业补充练习2、袋中装有4个白棋子、3个黑棋子,从袋中随机地取棋
子,设取到一个白棋子得2分,取到一个黑棋子得1分,从袋中任取4个棋子.
(1)求得分X的分布列;
(2)求得分大于6的概率.
解:(1)袋中共7个棋子,以取到白棋子为标准,则取到白棋子的个数为1,2,3,4,对应的得分X为5,6,7,8.
由题意知,取到的白棋子数服从参数为N=7,M=4,n=4的超几何分布,故得分也服从该超几何分布.
