2.3.1 离散型随机变量的数学期望 课件(34张PPT)
文档属性
| 名称 | 2.3.1 离散型随机变量的数学期望 课件(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 582.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览










文档简介
课件34张PPT。2.3.1 离散型随机变量的数学期望课前准备:学案、课本、练习本、双色笔、还有你的激情哦!寄语同学:“既然确定更远的飞翔,就别再收回已经张开的翅膀”,永不言弃,突破黑暗,就会看到黎明的曙光!!!预习反馈一、复习回顾1. 离散型随机变量的分布列2. 离散型随机变量分布列的性质:(1) pi≥0,i=1,2,…;
(2) p1+p2+…+pi+…=1.3. 离散型随机变量的分布列:
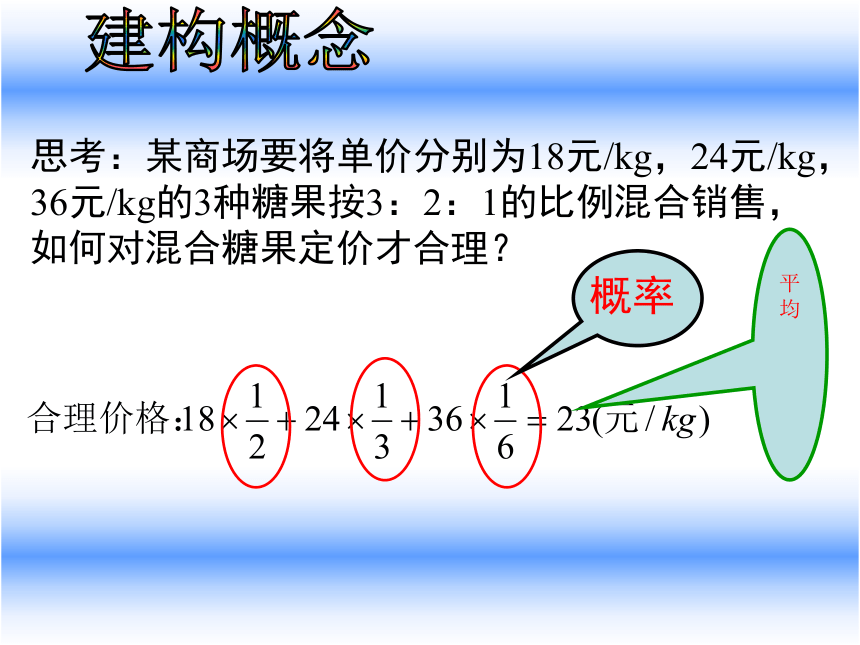
确定随机变量相关事件的概率。4、什么叫n次独立重复试验?一.复习回顾 一般地,由n次试验构成,且每次试验互相独立完成,每次试验的结果仅有两种对立的状态,即A与 ,每次试验中P(A)=p>0。称这样的试验为n次独立重复试验,也称伯努利试验。5、什么叫二项分布?若X~B (n,p)按3:2:1的比例混合 18元/kg ?混合糖果中每一粒糖果的质量都相等24元/kg 36元/kg 定价为混合糖果的平均价格才合理按3:2:1的比例混合 18元/kg 24元/kg 36元/kg 平均价格为
问题1:混合后,每1kg糖的平均价格为多少?问题2:若在混合糖果中任取一粒糖果,用随机变量
X表示这颗糖果的单价(元/kg),写出X的
分布列。某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?362418问题3: 作为顾客,买了1kg糖果要付23元,而顾客
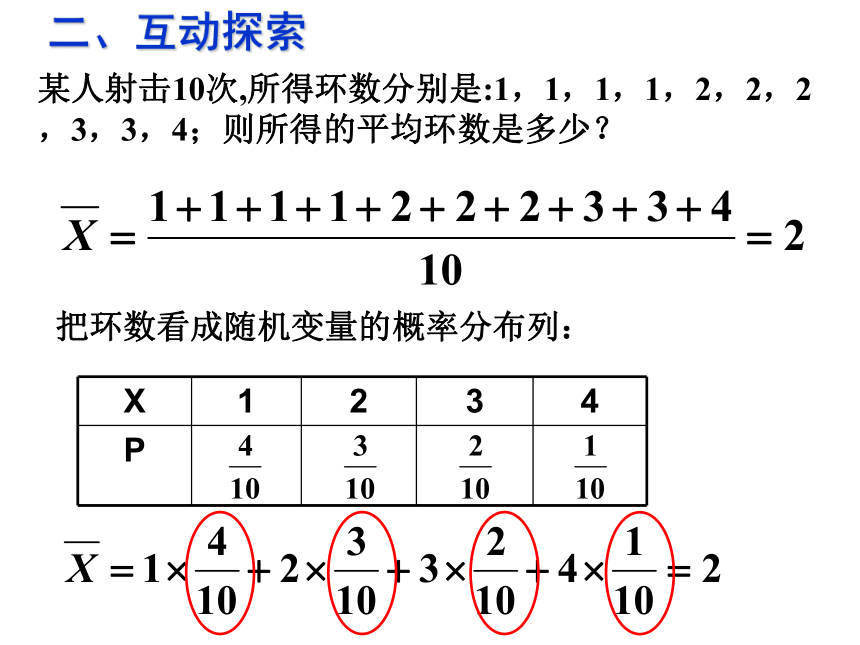
买的这1kg糖果的真实价格一定是23元吗??教学过程建构概念平均概率思考:某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?把环数看成随机变量的概率分布列:二、互动探索三、概念形成
1、离散型随机变量取值的平均值数学期望一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望.
它反映了离散型随机变量取值的平均水平.2、概念形成 离散型随机变量的数学期望(均值)几点说明:(1)均值或数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平。 (2)在有限取值离散型随机变量X的分布中,若p1=p2=p3=…=pn,此时
这说明数学期望与平均值具有相同的含义。例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?3、例题讲解一般地,如果随机变量X服从两点分布,则小结:例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2)证明:
所以若ξ~B(n,p),则Eξ=np. 证明:若ξ~B(n,p),则Eξ=np 一般地,如果随机变量X服从二项分布,即X~B(n,p),则小结:练一练: 一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .3例3.一个袋子里装有大小相同的3 个红球和2个黄球,从中摸出3个球.
(1)求得到黄球个数ξ的分布列;
(2)求ξ的期望。解:(1) ξ 服从超几何分布小结:一般地,如果随机变量X服从参数为N,M,n的超几何分布,则1、如果随机变量X服从两点分布,则2、如果随机变量X服从二项分布,即X~B(n,p),则3、如果随机变量X服从参数为N,M,n的超几何分布,即X~H(n,M,N),则
设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) EY=?思考:···············Y=aX+b即时训练:1、随机变量X的分布列是(1)则EX= . 2、随机变量ξ的分布列是2.4(2)若Y=2X+1,则EY= . 5.8Eξ=7.5,则a= b= .0.40.1反思:1、用定义求随机变量均值的一般步骤:1)找出随机变量的可能取值;反思:2、求随机变量均值的一般方法:1)利用定义求均值;2)求出分布列3)利用定义(公式)求均值。2)利用线性性质求均值。3)两点分布,二项分布,超几何分布直接用公式求均值。根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01.该地区某工地上有一台大型设备,遇到大洪水时损失60000元,遇到小洪水损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元;
方案2:建保护围墙,建设费为2000元,
但围墙只能防小洪水;
方案3:不采取任何措施,希望不发生洪水.
试比较哪一种方案好?练习1解 用x1、x2和x3分别表示三种方案的损失.
采用第一种方案,无论有无洪水,都损失3 800元,即x1=3 800.
采用第二种方案,遇到大洪水时,损失2 000+60 000=62 000元;
没有大洪水时,损失2 000元,即
同样,采用第三种方案,有
于是,
Ex1=3 800,
Ex2=62 000×P(x2=62 000)+2 000×P(x2=2 000)=62 000×0.01+2 000×(1-0.01)=2 600,
Ex3=60 000×P(x3=60 000)+10 000×P(x3=10 000)+0×P(x3=0)
=60 000×0.01+10 000×0.25=3 100.
采用方案二的平均损失最小,所以可以选择方案二.练2 一次单元测验由20个选择题构成,每个选择题有4个选项.其中仅有一个选项正确,每题选对得5分.不选或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从各选项中随机地选择一个.分别求学生甲和学生乙在这次测验中的成绩的均值.思路分析:设甲、乙选对题数分别为X1、X2,则甲、乙两人的成绩分别为Y1= 5X1、Y2= 5X2, 问题转化为求:E(Y1)= E(5X1)=
E(Y2) =E(5X2)=思考:X1、X2服从什么分布?5E(X1)5E(X2)解: 设学生甲和学生乙在这次单元测验中选对的题数分别是X1和X2,则 X1~B(20,0.9),
X2~B(20,0.25),
EX1=20×0.9=18,
EX2=20×0.25=5.
由于答对每题得5分,学生甲和学生乙在这次测验中的成绩分别是5X1和5X2。所以,他们在测验中的成绩的期望分别是
E(5X1)=5EX1=5×18=90,
E(5X2)=5EX2=5×5=25.
归纳总结应用概念步骤期望的概念期望为我们提供了实际问题决策的理论依据。求期望的三个步骤 方法求期望的三种方法五、课堂小结一、离散型随机变量取值的平均值数学期望二、数学期望的性质三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则五、如果随机变量X服从参数为N,M,n的超几何分布,即X~H(n,M,N),则布置作业基础题能力题课后探究题必做题书p70:2,3
选做题p70:1,4高考链接16年全国卷18题证明超几何分布均值公式
谢谢!
(2) p1+p2+…+pi+…=1.3. 离散型随机变量的分布列:
确定随机变量相关事件的概率。4、什么叫n次独立重复试验?一.复习回顾 一般地,由n次试验构成,且每次试验互相独立完成,每次试验的结果仅有两种对立的状态,即A与 ,每次试验中P(A)=p>0。称这样的试验为n次独立重复试验,也称伯努利试验。5、什么叫二项分布?若X~B (n,p)按3:2:1的比例混合 18元/kg ?混合糖果中每一粒糖果的质量都相等24元/kg 36元/kg 定价为混合糖果的平均价格才合理按3:2:1的比例混合 18元/kg 24元/kg 36元/kg 平均价格为
问题1:混合后,每1kg糖的平均价格为多少?问题2:若在混合糖果中任取一粒糖果,用随机变量
X表示这颗糖果的单价(元/kg),写出X的
分布列。某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?362418问题3: 作为顾客,买了1kg糖果要付23元,而顾客
买的这1kg糖果的真实价格一定是23元吗??教学过程建构概念平均概率思考:某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?把环数看成随机变量的概率分布列:二、互动探索三、概念形成
1、离散型随机变量取值的平均值数学期望一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望.
它反映了离散型随机变量取值的平均水平.2、概念形成 离散型随机变量的数学期望(均值)几点说明:(1)均值或数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平。 (2)在有限取值离散型随机变量X的分布中,若p1=p2=p3=…=pn,此时
这说明数学期望与平均值具有相同的含义。例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?3、例题讲解一般地,如果随机变量X服从两点分布,则小结:例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2)证明:
所以若ξ~B(n,p),则Eξ=np. 证明:若ξ~B(n,p),则Eξ=np 一般地,如果随机变量X服从二项分布,即X~B(n,p),则小结:练一练: 一个袋子里装有大小相同的3 个红球和2个黄球,从中有放回地取5次,则取到红球次数的数学期望是 .3例3.一个袋子里装有大小相同的3 个红球和2个黄球,从中摸出3个球.
(1)求得到黄球个数ξ的分布列;
(2)求ξ的期望。解:(1) ξ 服从超几何分布小结:一般地,如果随机变量X服从参数为N,M,n的超几何分布,则1、如果随机变量X服从两点分布,则2、如果随机变量X服从二项分布,即X~B(n,p),则3、如果随机变量X服从参数为N,M,n的超几何分布,即X~H(n,M,N),则
设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) EY=?思考:···············Y=aX+b即时训练:1、随机变量X的分布列是(1)则EX= . 2、随机变量ξ的分布列是2.4(2)若Y=2X+1,则EY= . 5.8Eξ=7.5,则a= b= .0.40.1反思:1、用定义求随机变量均值的一般步骤:1)找出随机变量的可能取值;反思:2、求随机变量均值的一般方法:1)利用定义求均值;2)求出分布列3)利用定义(公式)求均值。2)利用线性性质求均值。3)两点分布,二项分布,超几何分布直接用公式求均值。根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01.该地区某工地上有一台大型设备,遇到大洪水时损失60000元,遇到小洪水损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元;
方案2:建保护围墙,建设费为2000元,
但围墙只能防小洪水;
方案3:不采取任何措施,希望不发生洪水.
试比较哪一种方案好?练习1解 用x1、x2和x3分别表示三种方案的损失.
采用第一种方案,无论有无洪水,都损失3 800元,即x1=3 800.
采用第二种方案,遇到大洪水时,损失2 000+60 000=62 000元;
没有大洪水时,损失2 000元,即
同样,采用第三种方案,有
于是,
Ex1=3 800,
Ex2=62 000×P(x2=62 000)+2 000×P(x2=2 000)=62 000×0.01+2 000×(1-0.01)=2 600,
Ex3=60 000×P(x3=60 000)+10 000×P(x3=10 000)+0×P(x3=0)
=60 000×0.01+10 000×0.25=3 100.
采用方案二的平均损失最小,所以可以选择方案二.练2 一次单元测验由20个选择题构成,每个选择题有4个选项.其中仅有一个选项正确,每题选对得5分.不选或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从各选项中随机地选择一个.分别求学生甲和学生乙在这次测验中的成绩的均值.思路分析:设甲、乙选对题数分别为X1、X2,则甲、乙两人的成绩分别为Y1= 5X1、Y2= 5X2, 问题转化为求:E(Y1)= E(5X1)=
E(Y2) =E(5X2)=思考:X1、X2服从什么分布?5E(X1)5E(X2)解: 设学生甲和学生乙在这次单元测验中选对的题数分别是X1和X2,则 X1~B(20,0.9),
X2~B(20,0.25),
EX1=20×0.9=18,
EX2=20×0.25=5.
由于答对每题得5分,学生甲和学生乙在这次测验中的成绩分别是5X1和5X2。所以,他们在测验中的成绩的期望分别是
E(5X1)=5EX1=5×18=90,
E(5X2)=5EX2=5×5=25.
归纳总结应用概念步骤期望的概念期望为我们提供了实际问题决策的理论依据。求期望的三个步骤 方法求期望的三种方法五、课堂小结一、离散型随机变量取值的平均值数学期望二、数学期望的性质三、如果随机变量X服从两点分布,则四、如果随机变量X服从二项分布,即X~B(n,p),则五、如果随机变量X服从参数为N,M,n的超几何分布,即X~H(n,M,N),则布置作业基础题能力题课后探究题必做题书p70:2,3
选做题p70:1,4高考链接16年全国卷18题证明超几何分布均值公式
谢谢!
