2.3.1 离散型随机变量的数学期望 课件(23张PPT)
文档属性
| 名称 | 2.3.1 离散型随机变量的数学期望 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:47:57 | ||
图片预览






文档简介
课件23张PPT。离散型随机变量的数学期望 A, B两人赌技相同,各押赌注32个金币,规定先胜三局者为胜,赌博进行了一段时间,A赌徒已胜2局,B赌徒胜1局,发生意外,赌博中断。A赌徒B赌徒实力相当一、创设情境 引入新课两人该如何分这64金币? A, B两人赌技相同,各押赌注32个金币,规定先胜三局者为胜,赌博进行了一段时间,A赌徒已胜2局,B赌徒胜1局,发生意外,赌博中断。两人该如何分配这64个金币?比赛5局必能决出胜负。因此后两局可能的比赛结果A赌徒
{(胜,胜),(胜,负),(负,胜),(负,负)},
结合前3局已知结果,A赌徒至少胜一局即可获胜,由于两人
赌技相同,故A赌徒获胜的概率为3/4,因此分A赌徒
48金币,B赌徒16金币更为合理。问题1:混合后,每1kg糖的平均价格为多少?问题2:若在混合糖果中任取一粒糖果,用随机变量
X表示这颗糖果的单价(元/kg),写出X的
分布列。探索1、某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?362418问题3: 作为顾客,买了1kg糖果要付23元,而顾客
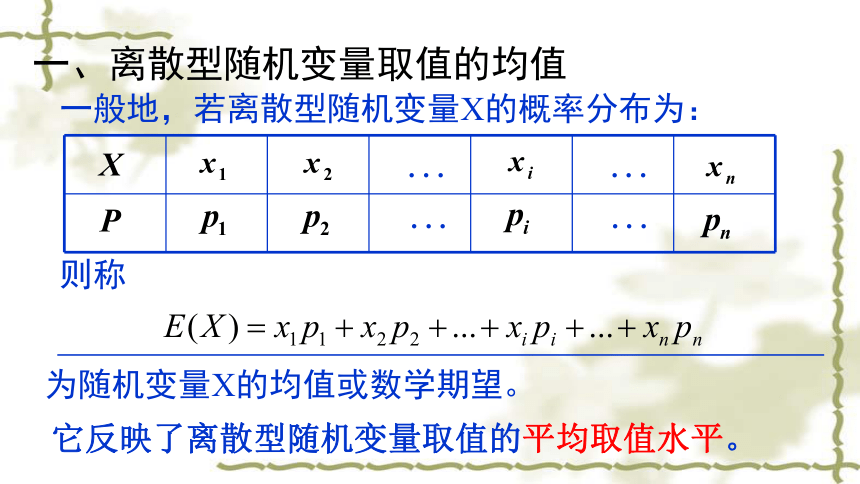
买的这1kg糖果的真实价格一定是23元吗?二、互动探索一、离散型随机变量取值的均值一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均取值水平。1、随机变量X的概率分布为:求X的数学期望。2、盒子中放有大小形状完全相同的标号为1,2,3,4,5的5个小球,一次从盒中取出3个小球,写出小球最大标号X的分布列和数学期望?练一练(1)问题4:离散型随机变量X的期望与X可能取值的算术平均数相同吗?
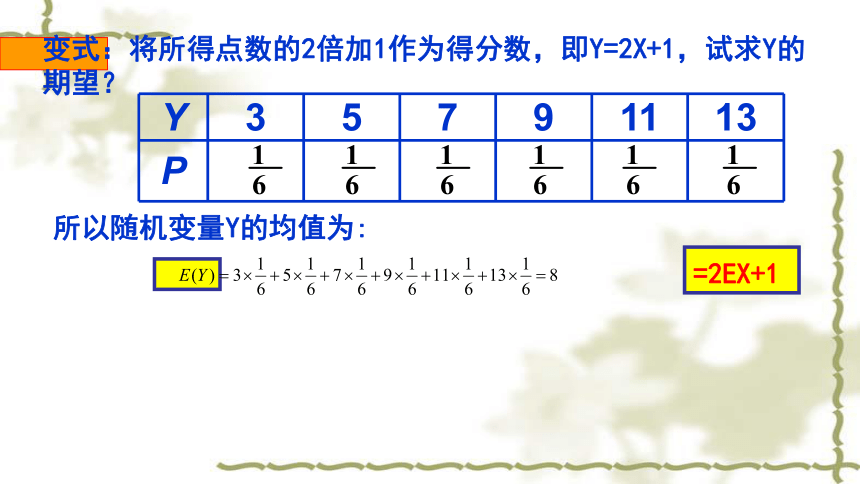
期望的计算是从概率分布出发,因而它是概率意义下的平均值。随机变量X取每个值时概率不同导致了期望不同于初中所学的算术平均数。问题5:离散型随机变量X的期望与X可能取值的算术平均数何时相等?探索2:随机抛掷一个骰子,求所得骰子的点数X的期望。 变式:将所得点数的2倍加1作为得分数,即Y=2X+1,试求Y的 期望?所以随机变量Y的均值为:设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) E(Y)=?思考:···············Y=aX+b一、离散型随机变量取值的均值二、随机变量数学期望的性质(线性性质)1、随机变量X的分布列是(1)则E(X)= . 2、随机变量ξ的分布列是2.4(2)若Y=2X+1,则E(Y)= . 5.8E(ξ)=7.5,则a= b= .0.40.1练一练(2)例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则三、例题讲解两点分布的期望三、例题讲解变式1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他连续罚球3次的得分X的均值是多少?分析: X~B(3,0.7)例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?三、例题讲解变式2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为p,则他连续罚球n次的得分X的均值是多少?X的分布列如下:分析: X~B(n,p)证明:证明:若X~B(n,p),则E(X)=np 2;一般地,如果随机变量X服从二项分布,即X~B(n,p),则E(X)=np结论:1;一般地,如果随机变量X服从
两点分布(1,p),则E(X)=p例2.一个袋子里装有大小相同的3 个红球和2个黄球,从中摸出3个球.(不放回取3次,每次取1球)
(1)求得到黄球个数ξ的分布列;
(2)求ξ的期望。小结:超几何分布的数学期望变式2. 若上述取球改有放回取3次,每次取1球呢?例3. 假如你 是一位商场经理,在五一那天想举行促销活动,根据统计资料显示,若在商场内举行促销活动,可获利2万元;若在商场外举行促销活动,则要看天气情况:不下雨可获利10万元,下雨则要损失4万元。气象台预报五一那天有雨的概率是40%,你应选择哪种促销方式?解:设商场在商场外的促销活动中获
得经济效益为X万元,则X的分布列为0.40.6-410E (X) = 10×0.6+(-4) ×0.4 = 4.4万元>2万元,故应选择在商场外搞促销活动。反思:1、用定义求随机变量均值的一般步骤:1)找出随机变量的可能取值;反思:2、求随机变量均值的一般方法:1)利用定义求均值;2)求出分布列3)利用定义(公式)求均值。2)利用线性性质求均值。3)两点分布,二项分布直接用公式求均值。归纳总结应用概念步骤期望的概念期望为我们提供了实际问题决策的理论依据。求期望的三个步骤 方法求期望的三种方法布置作业谢谢!
{(胜,胜),(胜,负),(负,胜),(负,负)},
结合前3局已知结果,A赌徒至少胜一局即可获胜,由于两人
赌技相同,故A赌徒获胜的概率为3/4,因此分A赌徒
48金币,B赌徒16金币更为合理。问题1:混合后,每1kg糖的平均价格为多少?问题2:若在混合糖果中任取一粒糖果,用随机变量
X表示这颗糖果的单价(元/kg),写出X的
分布列。探索1、某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售,如何对混合糖果定价才合理?362418问题3: 作为顾客,买了1kg糖果要付23元,而顾客
买的这1kg糖果的真实价格一定是23元吗?二、互动探索一、离散型随机变量取值的均值一般地,若离散型随机变量X的概率分布为:则称为随机变量X的均值或数学期望。它反映了离散型随机变量取值的平均取值水平。1、随机变量X的概率分布为:求X的数学期望。2、盒子中放有大小形状完全相同的标号为1,2,3,4,5的5个小球,一次从盒中取出3个小球,写出小球最大标号X的分布列和数学期望?练一练(1)问题4:离散型随机变量X的期望与X可能取值的算术平均数相同吗?
期望的计算是从概率分布出发,因而它是概率意义下的平均值。随机变量X取每个值时概率不同导致了期望不同于初中所学的算术平均数。问题5:离散型随机变量X的期望与X可能取值的算术平均数何时相等?探索2:随机抛掷一个骰子,求所得骰子的点数X的期望。 变式:将所得点数的2倍加1作为得分数,即Y=2X+1,试求Y的 期望?所以随机变量Y的均值为:设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) E(Y)=?思考:···············Y=aX+b一、离散型随机变量取值的均值二、随机变量数学期望的性质(线性性质)1、随机变量X的分布列是(1)则E(X)= . 2、随机变量ξ的分布列是2.4(2)若Y=2X+1,则E(Y)= . 5.8E(ξ)=7.5,则a= b= .0.40.1练一练(2)例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则三、例题讲解两点分布的期望三、例题讲解变式1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他连续罚球3次的得分X的均值是多少?分析: X~B(3,0.7)例1.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?三、例题讲解变式2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为p,则他连续罚球n次的得分X的均值是多少?X的分布列如下:分析: X~B(n,p)证明:证明:若X~B(n,p),则E(X)=np 2;一般地,如果随机变量X服从二项分布,即X~B(n,p),则E(X)=np结论:1;一般地,如果随机变量X服从
两点分布(1,p),则E(X)=p例2.一个袋子里装有大小相同的3 个红球和2个黄球,从中摸出3个球.(不放回取3次,每次取1球)
(1)求得到黄球个数ξ的分布列;
(2)求ξ的期望。小结:超几何分布的数学期望变式2. 若上述取球改有放回取3次,每次取1球呢?例3. 假如你 是一位商场经理,在五一那天想举行促销活动,根据统计资料显示,若在商场内举行促销活动,可获利2万元;若在商场外举行促销活动,则要看天气情况:不下雨可获利10万元,下雨则要损失4万元。气象台预报五一那天有雨的概率是40%,你应选择哪种促销方式?解:设商场在商场外的促销活动中获
得经济效益为X万元,则X的分布列为0.40.6-410E (X) = 10×0.6+(-4) ×0.4 = 4.4万元>2万元,故应选择在商场外搞促销活动。反思:1、用定义求随机变量均值的一般步骤:1)找出随机变量的可能取值;反思:2、求随机变量均值的一般方法:1)利用定义求均值;2)求出分布列3)利用定义(公式)求均值。2)利用线性性质求均值。3)两点分布,二项分布直接用公式求均值。归纳总结应用概念步骤期望的概念期望为我们提供了实际问题决策的理论依据。求期望的三个步骤 方法求期望的三种方法布置作业谢谢!
