2.3.1 离散型随机变量的数学期望 课件(18张PPT)
文档属性
| 名称 | 2.3.1 离散型随机变量的数学期望 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 735.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览






文档简介
课件18张PPT。 离散型随机变量的均值一、温故知新1、离散型随机变量的分布列2、离散型随机变量分布列的性质:(1)pi≥0,i=1,2,…;
(2)p1+p2+…+pn=1.教学目标:
1.通过事例理解离散型随机变量均值的概念,能计算简单的随机变量的均值。
2.通过探究概念的过程,体会由具体到抽象的数学探究方法。
3.通过本节的学习,进一步感受数学的应用价值,提高数学的应用意识。
教学重点:
离散型随机变量均值
教学难点:
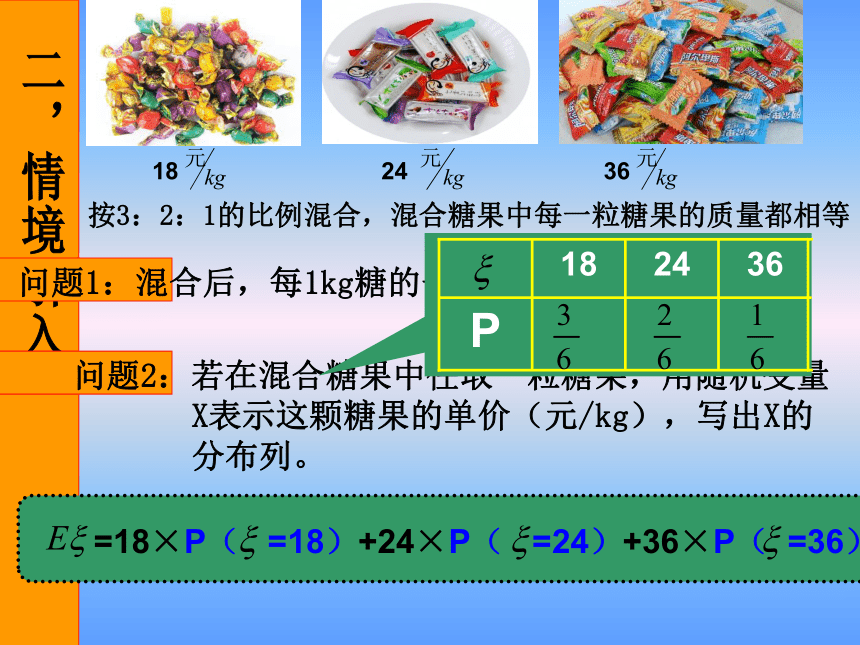
求解离散型随机变量均值按3:2:1的比例混合,混合糖果中每一粒糖果的质量都相等
问题1:混合后,每1kg糖的平均价格定为多少合理?问题2:若在混合糖果中任取一粒糖果,用随机变量
X表示这颗糖果的单价(元/kg),写出X的
分布列。1 一般地,若离散型随机变量的概率分布为则称
为 的数学期望或均值,它反映了随机变量取值的
平均水平.三,新知获得概括定义设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) E(Y)=?2 思考:······························历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9.
例1:(2012高考湖北理)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:求:工期延误天数 Y 的均值。
四、例题讲解解:由已知条件和概率的加法公式有:.
所以的分布列为: 于是故工期延误天数Y的值为3. 当堂训练
1.甲、乙两名射手一次射击中的得分为两个相互独立的甲、乙两人谁的射击水平高?随机变量例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则五、深入理解 探究性质小结:例3.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2)一般地,如果随机变量X服从二项分布,即X~B(n,p),则小结:一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分。学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和学生乙在这次英语单元测验中的成绩的均值。 例题4解: 设学生甲和学生乙在这次英语测验中选择了正确答案的选择题个数分别是ξ和η,则 ξ~B(20,0.9),
η~B(20,0.25),
Eξ=20×0.9=18,
Eη=20×0.25=5.
由于答对每题得5分,学生甲和乙在这次英语测验中的成绩分别是5ξ和5η。所以,他们在测验中的成绩的均值分别是
E(5ξ)=5Eξ=5×18=90,
E(5η)=5Eη=5×5=25.
1、离散型随机变量均值的定义一般地,若离散型随机变量X的概率分布为 则称 为随机变量
X的均值或数学期望,数学期望又简称为期望。 六,课堂小 结2、离散型随机变量均值的性质(1)随机变量均值的线性性质 若ξ~B(n,p),则E(ξ)= np(2)服从两点分布的均值(3)服从二项分布的均值 若ξ~B(1,p), 则E(ξ)= p八,作业布置习题2.3 第1,2题。谢谢大家!
(2)p1+p2+…+pn=1.教学目标:
1.通过事例理解离散型随机变量均值的概念,能计算简单的随机变量的均值。
2.通过探究概念的过程,体会由具体到抽象的数学探究方法。
3.通过本节的学习,进一步感受数学的应用价值,提高数学的应用意识。
教学重点:
离散型随机变量均值
教学难点:
求解离散型随机变量均值按3:2:1的比例混合,混合糖果中每一粒糖果的质量都相等
问题1:混合后,每1kg糖的平均价格定为多少合理?问题2:若在混合糖果中任取一粒糖果,用随机变量
X表示这颗糖果的单价(元/kg),写出X的
分布列。1 一般地,若离散型随机变量的概率分布为则称
为 的数学期望或均值,它反映了随机变量取值的
平均水平.三,新知获得概括定义设Y=aX+b,其中a,b为常数,则Y也是随机变量.
(1) Y的分布列是什么?
(2) E(Y)=?2 思考:······························历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9.
例1:(2012高考湖北理)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:求:工期延误天数 Y 的均值。
四、例题讲解解:由已知条件和概率的加法公式有:.
所以的分布列为: 于是故工期延误天数Y的值为3. 当堂训练
1.甲、乙两名射手一次射击中的得分为两个相互独立的甲、乙两人谁的射击水平高?随机变量例2.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,则他罚球1次的得分X的均值是多少?一般地,如果随机变量X服从两点分布,则五、深入理解 探究性质小结:例3.篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,他连续罚球3次;
(1)求他得到的分数X的分布列;
(2)求X的期望。解:(1) X~B(3,0.7)(2)一般地,如果随机变量X服从二项分布,即X~B(n,p),则小结:一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分。学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一个。求学生甲和学生乙在这次英语单元测验中的成绩的均值。 例题4解: 设学生甲和学生乙在这次英语测验中选择了正确答案的选择题个数分别是ξ和η,则 ξ~B(20,0.9),
η~B(20,0.25),
Eξ=20×0.9=18,
Eη=20×0.25=5.
由于答对每题得5分,学生甲和乙在这次英语测验中的成绩分别是5ξ和5η。所以,他们在测验中的成绩的均值分别是
E(5ξ)=5Eξ=5×18=90,
E(5η)=5Eη=5×5=25.
1、离散型随机变量均值的定义一般地,若离散型随机变量X的概率分布为 则称 为随机变量
X的均值或数学期望,数学期望又简称为期望。 六,课堂小 结2、离散型随机变量均值的性质(1)随机变量均值的线性性质 若ξ~B(n,p),则E(ξ)= np(2)服从两点分布的均值(3)服从二项分布的均值 若ξ~B(1,p), 则E(ξ)= p八,作业布置习题2.3 第1,2题。谢谢大家!
