3.1独立性检验 课件(22张PPT)
文档属性
| 名称 | 3.1独立性检验 课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 641.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:51:41 | ||
图片预览





文档简介
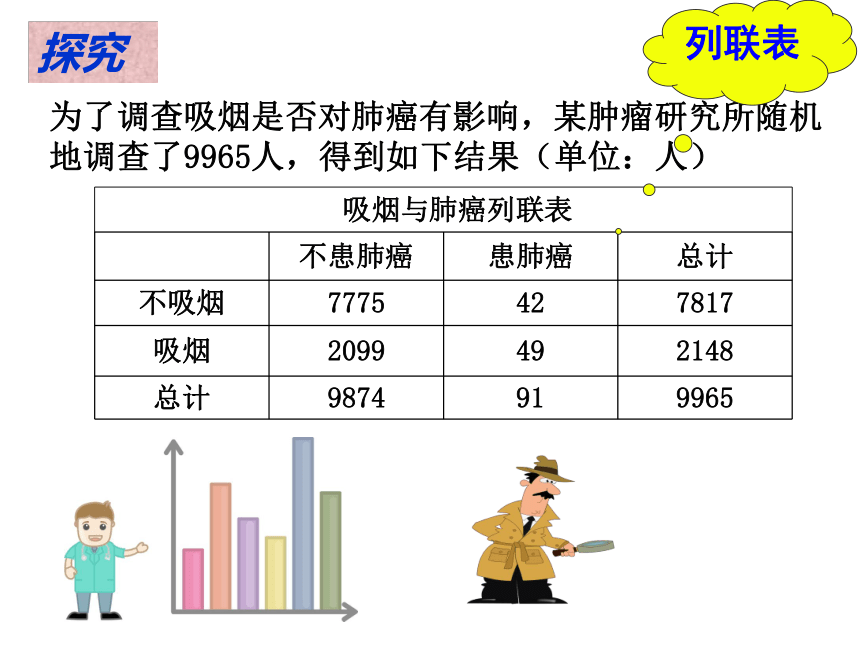
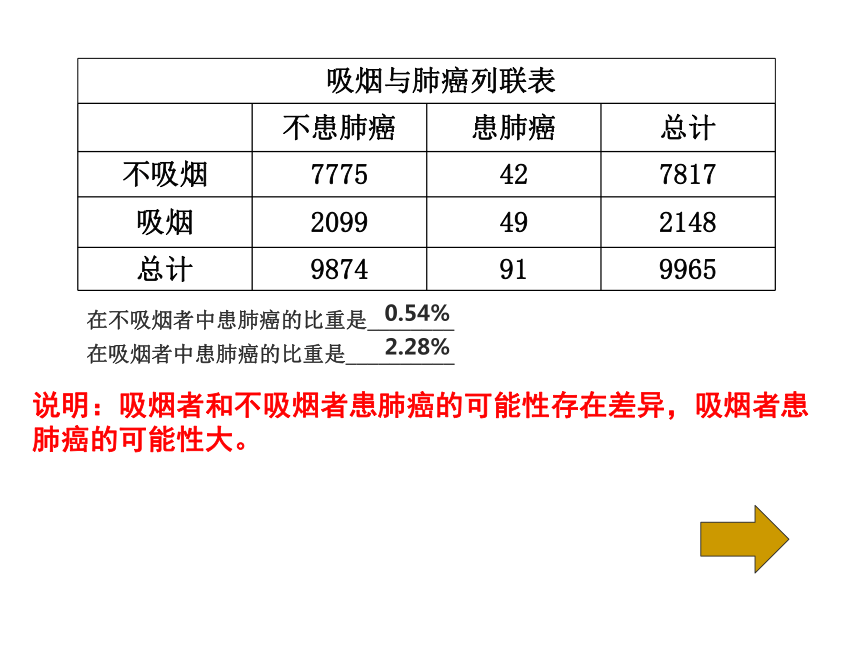
课件22张PPT。3.1独立性检验高二数学 选修2-3 第三章 统计案例如果要研究吸烟与患肺癌是否有关系,我们需要什么数据,可否将你想要的数据列成表格便于查看?得到数据后你准备如何对数据进行分析?为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)列联表探究在吸烟者中患肺癌的比重是__________ 0.54%2.28%说明:吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者患肺癌的可能性大。在不吸烟者中患肺癌的比重是________ 用A表示吸烟,B表示患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”,即P(AB)=P(A)P(B).因此|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;
|ad-bc|越大,说明吸烟与患肺癌之间关系越强。在表中,a恰好为事件AB发生的频数;a+b和a+c恰好分别为事件A和B发生的频数。由于频率接近于概率,所以在AB相互独立思维条件下应该有在一次恶劣气候的飞行航行中调查男女乘客在机上晕机的情况如下表所示,
据此资料你是否因为在恶劣气候飞行中男性比女性更容易晕机?
甲同学说:
因为男性晕机的人所占比例
女性晕机的人所占比例为
乙同学说:
因为P(A1B1)= 与 P(A1) P(B1)=
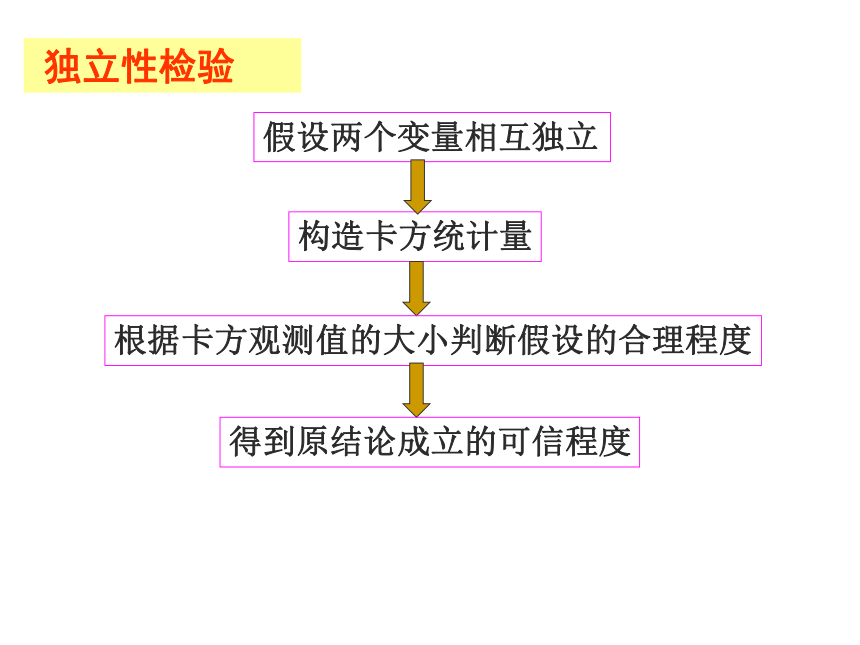
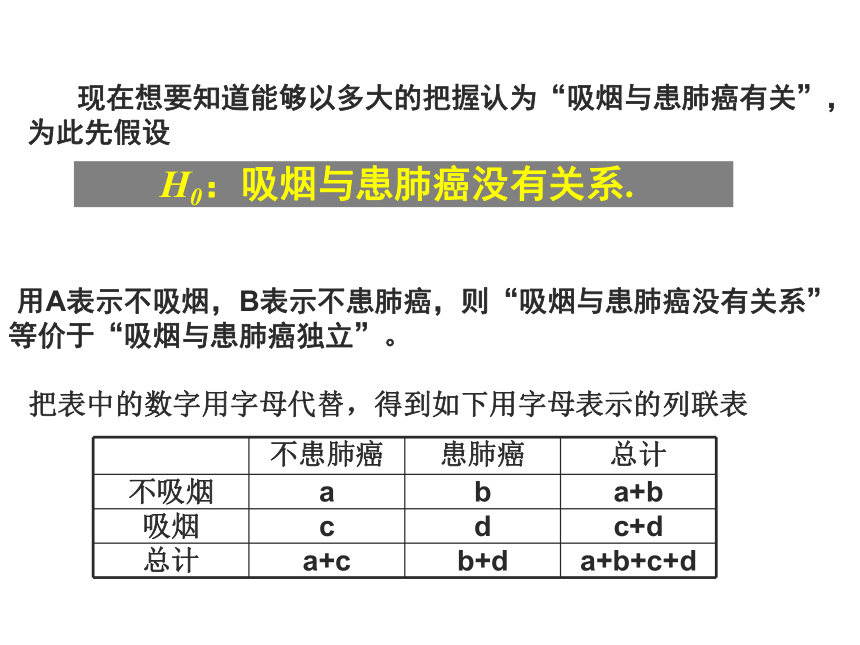
两者差距比较大,所以认为晕机与性别有关。差距不大,所以认为晕机与性别无关。假设两个变量相互独立构造卡方统计量根据卡方观测值的大小判断假设的合理程度得到原结论成立的可信程度 独立性检验 现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,
为此先假设 H0:吸烟与患肺癌没有关系.把表中的数字用字母代替,得到如下用字母表示的列联表 用A表示不吸烟,B表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”。 为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量-----卡方统计量(1)那么这个值到底能告诉我们什么呢? 卡方统计量作为检验在多大程度上可以认为“两个变量有关系”的标准分析:卡方越小,|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;
卡方越大,|ad-bc|越大,说明吸烟与患肺癌之间关系越强.思考:卡方大小的标准是什么呢? 在假设成立,即“吸烟与患肺癌没有关系”成立的前提下,
则卡方应该很小.故,当卡方很小时,说明在一定可信程度上假设成立,即“吸烟与患肺癌没有关系”成立
当卡方很大时,说明没有充分的证据说明假设成立,即没有充分的证据说明“吸烟与患肺癌没有关系”成立,即“吸烟与患肺癌没有关系”不成立,即“吸烟与患肺癌有关系”成立。
H0:吸烟与患肺癌没有关系.在H0成立的情况下,统计学家估算出如下的概率
即在H0成立的情况下,K2的值大于6.635的概率非常小,近似于0.01。 也就是说,在H0成立的情况下,对随机变量K2进行多次观测,观测值超过6.635的频率约为0.01。思考
答:判断出错的概率为0.01。两个临界值:3.841与6.635如果 就认为没有充分的证据说明变量A和B是有关系,即变量A和B是无关。
如果 就有95%的把握认为变量A和B是有关系;
如果 就有99%的把握认为变量A和B是有关系;
在犯错的概率不超过0.01的情况下认为变量A和B是有关系;假设两个变量相互独立构造卡方统计量根据卡方观测值的大小判断假设的合理程度得到原结论成立的可信程度 独立性检验1.给出下列实际问题:
①一种药物对某种病的治愈率;
②两种药物治疗同一种病是否有区别;
③吸烟者得肺病的概率;
④吸烟人群是否与性别有关系;
⑤上网与青少年的犯罪率是否有关系.
其中,用独立性检验可以解决的问题有___2.通过随机询问110名不同的大学生是否爱好某项运动 ,得到如下的列联表:
由
得到的正确结论是( )
有99%以上的把握认为“爱好该项运动与性别有关”
有99%以上的把握认为“爱好该项运动与性别无关”
在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
3.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若卡方的观测值为6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患肺病。
B.由独立性检验可知99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病。
C.若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指5%的可能性使得推判出现错误。
D.以上三种说法都不正确。4.网络对现代人的生活影响较大,尤其对青少年.为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生随机抽取了1000人调查,发现其中经常上网的有200人,其中有80人期末考试不及格,而另外800人中,有120人不及格.问:中学生经常往往是否影响学习?为什么?(你的结论正确率要达到99%)课堂小结1、了解独立性检验的应用范围及思想
2、利用 判断两个分类变量之间是否有关系问题: 数学家庞加莱每天都从一家面包店买一块1000g 的面包,并记录下买回的面包的实际质量。一年后,这位数学家发现,所记录数据的均值为950g。于是庞加莱推断这家面包店的面包分量不足。假设“面包份量足”,则一年购买面包的质量数据的平均值应该不少于1000g ;
“这个平均值不大于950g”是一个与假设“面包份量足”矛盾的小概率事件;
这个小概率事件的发生使庞加莱得出推断结果。独立性检验本节研究的是两个分类变量的独立性检验问题。在日常生活中,我们常常关心分类变量之间是否有关系:例如,吸烟是否与患肺癌有关系?
性别是否对于喜欢数学课程有影响?等等。
|ad-bc|越大,说明吸烟与患肺癌之间关系越强。在表中,a恰好为事件AB发生的频数;a+b和a+c恰好分别为事件A和B发生的频数。由于频率接近于概率,所以在AB相互独立思维条件下应该有在一次恶劣气候的飞行航行中调查男女乘客在机上晕机的情况如下表所示,
据此资料你是否因为在恶劣气候飞行中男性比女性更容易晕机?
甲同学说:
因为男性晕机的人所占比例
女性晕机的人所占比例为
乙同学说:
因为P(A1B1)= 与 P(A1) P(B1)=
两者差距比较大,所以认为晕机与性别有关。差距不大,所以认为晕机与性别无关。假设两个变量相互独立构造卡方统计量根据卡方观测值的大小判断假设的合理程度得到原结论成立的可信程度 独立性检验 现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,
为此先假设 H0:吸烟与患肺癌没有关系.把表中的数字用字母代替,得到如下用字母表示的列联表 用A表示不吸烟,B表示不患肺癌,则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”。 为了使不同样本容量的数据有统一的评判标准,基于上述分析,我们构造一个随机变量-----卡方统计量(1)那么这个值到底能告诉我们什么呢? 卡方统计量作为检验在多大程度上可以认为“两个变量有关系”的标准分析:卡方越小,|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;
卡方越大,|ad-bc|越大,说明吸烟与患肺癌之间关系越强.思考:卡方大小的标准是什么呢? 在假设成立,即“吸烟与患肺癌没有关系”成立的前提下,
则卡方应该很小.故,当卡方很小时,说明在一定可信程度上假设成立,即“吸烟与患肺癌没有关系”成立
当卡方很大时,说明没有充分的证据说明假设成立,即没有充分的证据说明“吸烟与患肺癌没有关系”成立,即“吸烟与患肺癌没有关系”不成立,即“吸烟与患肺癌有关系”成立。
H0:吸烟与患肺癌没有关系.在H0成立的情况下,统计学家估算出如下的概率
即在H0成立的情况下,K2的值大于6.635的概率非常小,近似于0.01。 也就是说,在H0成立的情况下,对随机变量K2进行多次观测,观测值超过6.635的频率约为0.01。思考
答:判断出错的概率为0.01。两个临界值:3.841与6.635如果 就认为没有充分的证据说明变量A和B是有关系,即变量A和B是无关。
如果 就有95%的把握认为变量A和B是有关系;
如果 就有99%的把握认为变量A和B是有关系;
在犯错的概率不超过0.01的情况下认为变量A和B是有关系;假设两个变量相互独立构造卡方统计量根据卡方观测值的大小判断假设的合理程度得到原结论成立的可信程度 独立性检验1.给出下列实际问题:
①一种药物对某种病的治愈率;
②两种药物治疗同一种病是否有区别;
③吸烟者得肺病的概率;
④吸烟人群是否与性别有关系;
⑤上网与青少年的犯罪率是否有关系.
其中,用独立性检验可以解决的问题有___2.通过随机询问110名不同的大学生是否爱好某项运动 ,得到如下的列联表:
由
得到的正确结论是( )
有99%以上的把握认为“爱好该项运动与性别有关”
有99%以上的把握认为“爱好该项运动与性别无关”
在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
3.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若卡方的观测值为6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患肺病。
B.由独立性检验可知99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病。
C.若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指5%的可能性使得推判出现错误。
D.以上三种说法都不正确。4.网络对现代人的生活影响较大,尤其对青少年.为了解网络对中学生学习成绩的影响,某地区教育主管部门从辖区初中生随机抽取了1000人调查,发现其中经常上网的有200人,其中有80人期末考试不及格,而另外800人中,有120人不及格.问:中学生经常往往是否影响学习?为什么?(你的结论正确率要达到99%)课堂小结1、了解独立性检验的应用范围及思想
2、利用 判断两个分类变量之间是否有关系问题: 数学家庞加莱每天都从一家面包店买一块1000g 的面包,并记录下买回的面包的实际质量。一年后,这位数学家发现,所记录数据的均值为950g。于是庞加莱推断这家面包店的面包分量不足。假设“面包份量足”,则一年购买面包的质量数据的平均值应该不少于1000g ;
“这个平均值不大于950g”是一个与假设“面包份量足”矛盾的小概率事件;
这个小概率事件的发生使庞加莱得出推断结果。独立性检验本节研究的是两个分类变量的独立性检验问题。在日常生活中,我们常常关心分类变量之间是否有关系:例如,吸烟是否与患肺癌有关系?
性别是否对于喜欢数学课程有影响?等等。
