1.3.1 ︳ax+b︳≤c,︳ax+b︳≥c型不等式的解法 课件(27张PPT)
文档属性
| 名称 | 1.3.1 ︳ax+b︳≤c,︳ax+b︳≥c型不等式的解法 课件(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 310.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:57:10 | ||
图片预览







文档简介
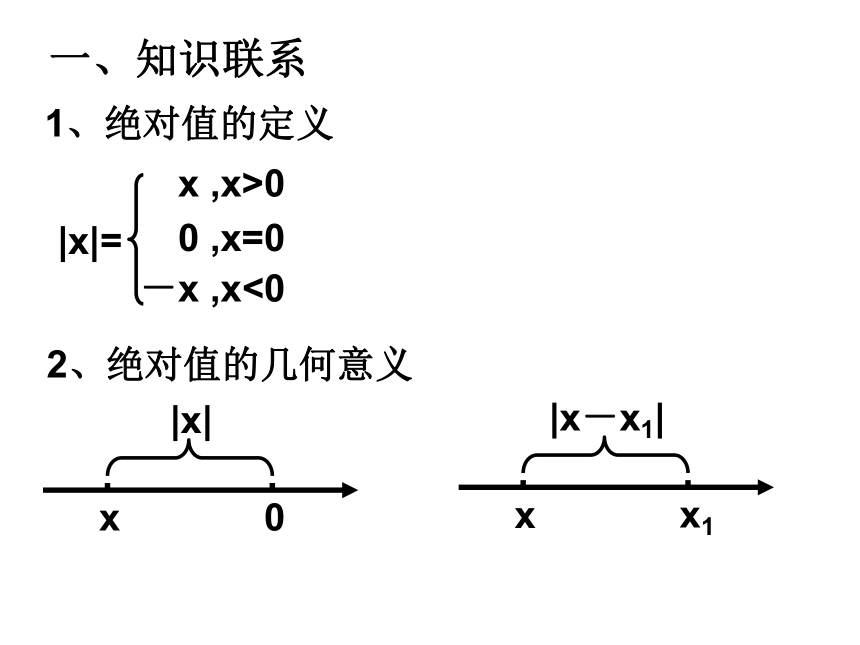
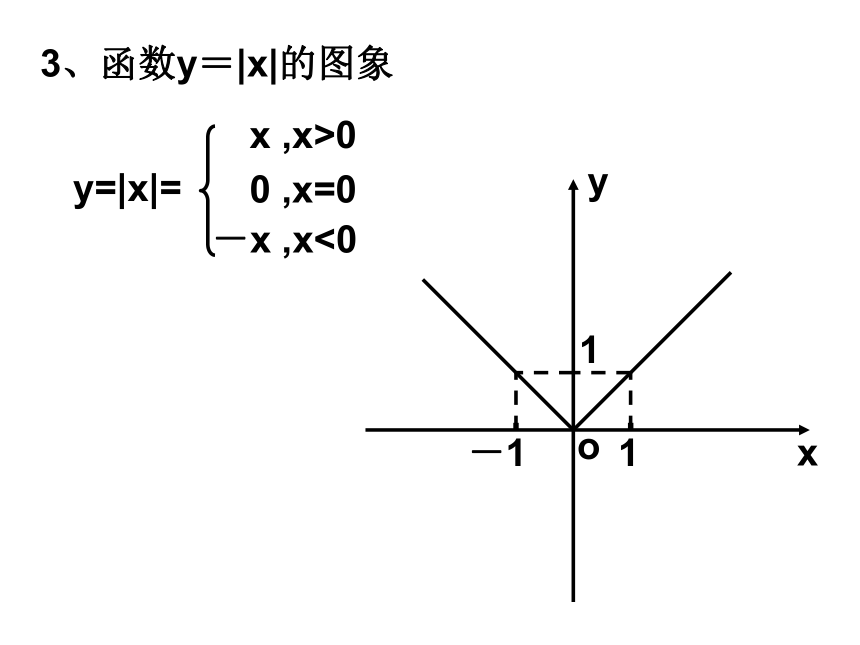
课件27张PPT。绝对值不等式的解法一、知识联系1、绝对值的定义|x|=x ,x>0-x ,x<00 ,x=02、绝对值的几何意义0x|x|x1x|x-x1|3、函数y=|x|的图象二、探索解法探索:不等式|x|<1的解集。方法一:利用绝对值的几何意义观察方法二:利用绝对值的定义去掉绝对值符号,需要分类讨论方法三:两边同时平方去掉绝对值符号方法四:利用函数图象观察这是解含绝对值不等式的四种常用思路 1 2 3 40-1不等式|x|<1的解集表示到原点的距离小于1的点的集合。1所以,不等式|x|<1的解集为{x|-1【解析】由|x-1|<2得-2<x-1<2,解得-1<x<3.
答案:(-1,3)(2)不等式|4-3x|≥2的解集是_____.
【解析】|4-3x|≥2?|3x-4|≥2?3x-4≤-2
或3x-4≥2,解得 或x≥2.
答案:题型3:形如n<| ax + b | <m (m>n>0)不等式等价于不等式组例2、解不等式 3<|3-2x|≤5 .例2 解不等式 3<|3-2x|≤5 .例2 解不等式 3<|3-2x|≤5 .① |f(x)||f(x)|② |f(x)|>g(x)型不等式
|f(x)|>g(x)?f(x)>g(x)或f(x)<-g(x)题型4:例3、解不等式|2x-1|<2-3x.例4、解不等式解:平方法例5、解不等式|x+1|+|x-1|≥3.题型:|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法.【思路点拨】 可用零点分段讨论,可用图象法,也可用绝对值几何意义求解.方法一:当x≤-1时,原不等式可以化为
-(x+1)-(x-1)≥3,解得
当-1<x<1时,原不等式可以化为
x+1-(x-1)≥3,即2≥3.不成立,无解.
当x≥1时,原不等式可以化为x+1+x-1≥3.所以
综上,可知原不等式的解集为例5、解不等式|x+1|+|x-1|≥3.方法二:将原不等式转化为|x+1|+|x-1|-3≥0.
构造函数y=|x+1|+|x-1|-3,即
作出函数的图象(如图).函数的零点是从图象可知当 或 时,y≥0.
即|x+1|+|x-1|-3≥0.
所以原不等式的解集为
例5、解不等式|x+1|+|x-1|≥3.解:方法三:如图,设数轴上与-1,1对应的点分别为A,B,那么
A,B两点间的距离为2,因此区间[-1,1]上的数都不是不等式
的解.设在A点左侧有一点A1到A,B两点的距离和为3,A1对应数
轴上的 .
同理设B点右侧有一点B1到A,B两点的距离和为3,B1对应数轴
上的 ,从数轴上可看到,
点A1的左边或点B1的右边的任何点到A,B的距离之和都大于3,
所以原不等式的解集是例5、解不等式|x+1|+|x-1|≥3.小结:|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法.
(1)利用绝对值不等式的几何意义求解,体现数形结合思想,
理解绝对值的几何意义,给绝对值不等式以准确的几何解释.
(2)以绝对值的零点为分界点,将数轴分为几个区间,利用“零
点分段法”求解,体现分类讨论的思想.确定各个绝对值符号
内多项式的_______性,进而去掉绝对值符号.
(3)通过构造函数,利用函数的图象求解,体现了函数与方程
的思想.正确求出函数的_____并画出函数图象(有时需要考查
函数的增减性)是关键. 正、负零点 (1)对任意x∈R,若|x-3|+|x+2|>a恒成立,求实数a的取值范围.
(2)关于x的不等式a>|x-3|+|x+2|的解集非空,求实数a的取值范围.
(3)关于x的不等式a>|x-3|+|x+2|在R上无解,求实数a的取值范围.形如|x+m|±|x+n|<(或>)a恒成立的问题【思路点拨】 对(1)(2)(3)来说,问题的关键是如何转化,求出函数f(x)=|x-3|+|x+2|的最值,则问题获解.【解】 (1)问题可转化为对一切x∈R恒有
a ∵f(x)=|x-3|+|x+2|≥|(x-3)-(x+2)|=5,
即f(x)min=5,∴a<5.
(2)问题可转化为a>f(x)的某些值,由题意a>f(x)min,同上得a>5.
(3)问题可转化为对一切x∈R恒有
a≤f(x)?a≤f(x)min,可知a≤5.四、小结(1)解含绝对值的不等式的关键是要去掉绝对值的符号,其基本思想是把含绝对值的不等式转为不含绝对值的不等式。(2)零点分段法解含有多个绝对值的不等式。谢谢!
答案:(-1,3)(2)不等式|4-3x|≥2的解集是_____.
【解析】|4-3x|≥2?|3x-4|≥2?3x-4≤-2
或3x-4≥2,解得 或x≥2.
答案:题型3:形如n<| ax + b | <m (m>n>0)不等式等价于不等式组例2、解不等式 3<|3-2x|≤5 .例2 解不等式 3<|3-2x|≤5 .例2 解不等式 3<|3-2x|≤5 .① |f(x)|
|f(x)|>g(x)?f(x)>g(x)或f(x)<-g(x)题型4:例3、解不等式|2x-1|<2-3x.例4、解不等式解:平方法例5、解不等式|x+1|+|x-1|≥3.题型:|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法.【思路点拨】 可用零点分段讨论,可用图象法,也可用绝对值几何意义求解.方法一:当x≤-1时,原不等式可以化为
-(x+1)-(x-1)≥3,解得
当-1<x<1时,原不等式可以化为
x+1-(x-1)≥3,即2≥3.不成立,无解.
当x≥1时,原不等式可以化为x+1+x-1≥3.所以
综上,可知原不等式的解集为例5、解不等式|x+1|+|x-1|≥3.方法二:将原不等式转化为|x+1|+|x-1|-3≥0.
构造函数y=|x+1|+|x-1|-3,即
作出函数的图象(如图).函数的零点是从图象可知当 或 时,y≥0.
即|x+1|+|x-1|-3≥0.
所以原不等式的解集为
例5、解不等式|x+1|+|x-1|≥3.解:方法三:如图,设数轴上与-1,1对应的点分别为A,B,那么
A,B两点间的距离为2,因此区间[-1,1]上的数都不是不等式
的解.设在A点左侧有一点A1到A,B两点的距离和为3,A1对应数
轴上的 .
同理设B点右侧有一点B1到A,B两点的距离和为3,B1对应数轴
上的 ,从数轴上可看到,
点A1的左边或点B1的右边的任何点到A,B的距离之和都大于3,
所以原不等式的解集是例5、解不等式|x+1|+|x-1|≥3.小结:|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法.
(1)利用绝对值不等式的几何意义求解,体现数形结合思想,
理解绝对值的几何意义,给绝对值不等式以准确的几何解释.
(2)以绝对值的零点为分界点,将数轴分为几个区间,利用“零
点分段法”求解,体现分类讨论的思想.确定各个绝对值符号
内多项式的_______性,进而去掉绝对值符号.
(3)通过构造函数,利用函数的图象求解,体现了函数与方程
的思想.正确求出函数的_____并画出函数图象(有时需要考查
函数的增减性)是关键. 正、负零点 (1)对任意x∈R,若|x-3|+|x+2|>a恒成立,求实数a的取值范围.
(2)关于x的不等式a>|x-3|+|x+2|的解集非空,求实数a的取值范围.
(3)关于x的不等式a>|x-3|+|x+2|在R上无解,求实数a的取值范围.形如|x+m|±|x+n|<(或>)a恒成立的问题【思路点拨】 对(1)(2)(3)来说,问题的关键是如何转化,求出函数f(x)=|x-3|+|x+2|的最值,则问题获解.【解】 (1)问题可转化为对一切x∈R恒有
a
即f(x)min=5,∴a<5.
(2)问题可转化为a>f(x)的某些值,由题意a>f(x)min,同上得a>5.
(3)问题可转化为对一切x∈R恒有
a≤f(x)?a≤f(x)min,可知a≤5.四、小结(1)解含绝对值的不等式的关键是要去掉绝对值的符号,其基本思想是把含绝对值的不等式转为不含绝对值的不等式。(2)零点分段法解含有多个绝对值的不等式。谢谢!
