1.3.1 ︳ax+b︳≤c,︳ax+b︳≥c型不等式的解法(一) 课件(15张PPT)
文档属性
| 名称 | 1.3.1 ︳ax+b︳≤c,︳ax+b︳≥c型不等式的解法(一) 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 882.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览




文档简介
课件15张PPT。绝对值不等式的解法
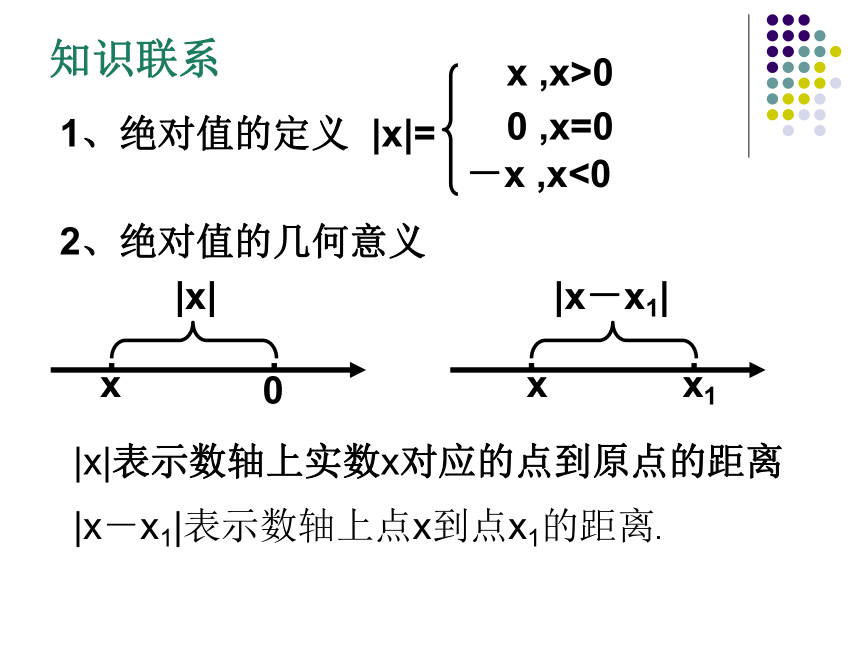
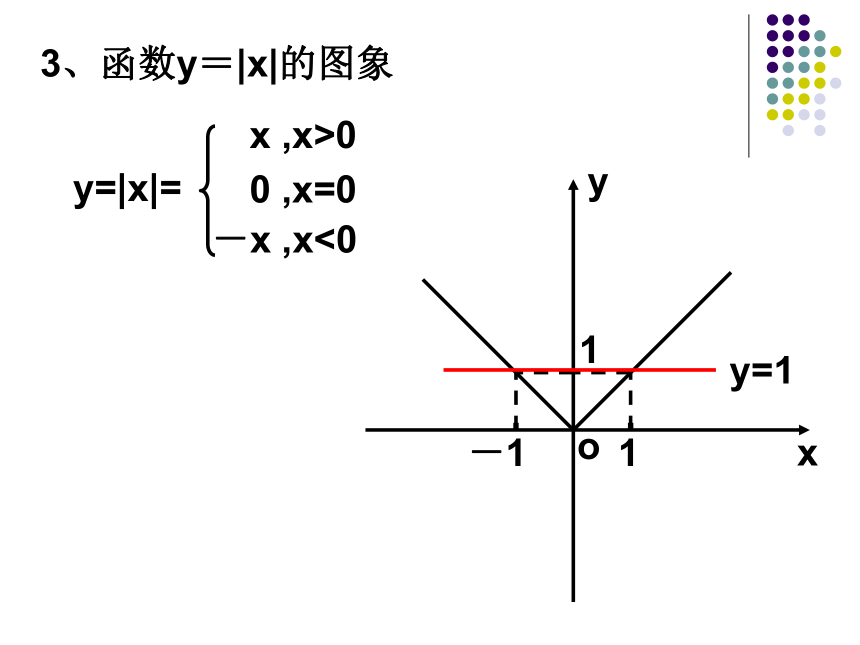
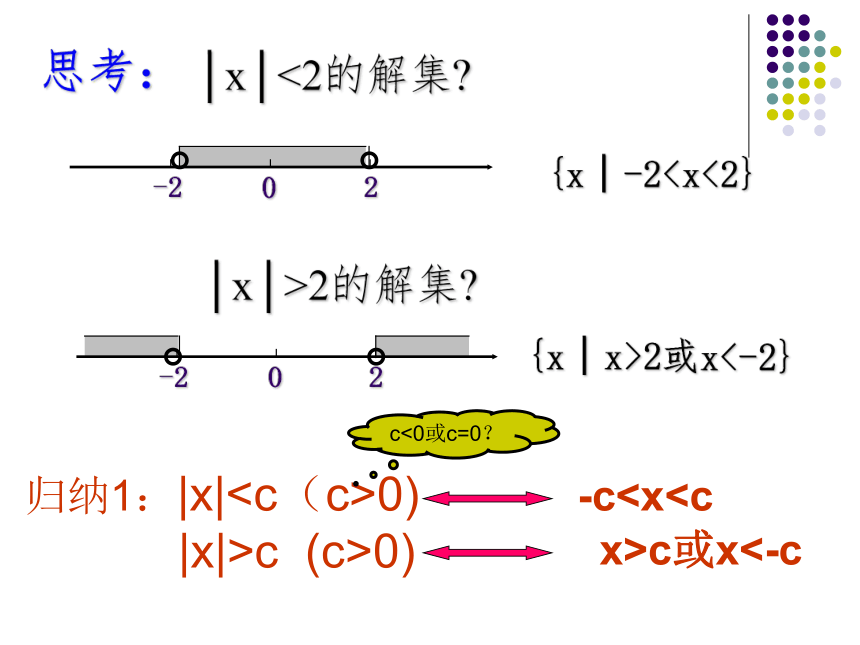
(第一课时)知识联系1、绝对值的定义|x|=x ,x>0-x ,x<00 ,x=02、绝对值的几何意义0x|x|x1x|x-x1||x|表示数轴上实数x对应的点到原点的距离|x-x1|表示数轴上点x到点x1的距离. 3、函数y=|x|的图象探索不等式|x|<1的解集?方法一:利用绝对值的几何意义观察方法二:利用绝对值的定义去掉绝对值符号,需要分类讨论方法三:两边同时平方去掉绝对值符号方法四:利用函数图象观察Z.x.x. K 3、函数y=|x|的图象y=1探索不等式|x|<1的解集?方法一:利用绝对值的几何意义观察方法二:利用绝对值的定义去掉绝对值符号,需要分类讨论方法三:两边同时平方去掉绝对值符号方法四:利用函数图象观察这是解含绝对值不等式的四种常用方法Z.x.x. K 类比:|x|<3的解|x|>3的解│x│<2的解集?思考: {x│-22的解集?{x│x>2或x<-2}归纳1:|x|0)
|x|>c (c>0) -cc或x<-cc<0或c=0?小结1:含绝对值不等式|x|c的解集例 解下列不等式 解:原不等式等价于整体换元解得 解得小结2:推广:
型如| f(x)|c (c>0) 不等式的解法例 解下列不等式 解:原不等式等价于整体换元解得 解得解下列不等式课堂小练:课堂小结:(2)相关点:绝对值的几何意义,
整体换元的思想,
不等式的性质
课堂延伸:解下列不等式课后作业: 优化方案P16-探究点1同学们再见!
(第一课时)知识联系1、绝对值的定义|x|=x ,x>0-x ,x<00 ,x=02、绝对值的几何意义0x|x|x1x|x-x1||x|表示数轴上实数x对应的点到原点的距离|x-x1|表示数轴上点x到点x1的距离. 3、函数y=|x|的图象探索不等式|x|<1的解集?方法一:利用绝对值的几何意义观察方法二:利用绝对值的定义去掉绝对值符号,需要分类讨论方法三:两边同时平方去掉绝对值符号方法四:利用函数图象观察Z.x.x. K 3、函数y=|x|的图象y=1探索不等式|x|<1的解集?方法一:利用绝对值的几何意义观察方法二:利用绝对值的定义去掉绝对值符号,需要分类讨论方法三:两边同时平方去掉绝对值符号方法四:利用函数图象观察这是解含绝对值不等式的四种常用方法Z.x.x. K 类比:|x|<3的解|x|>3的解│x│<2的解集?思考: {x│-2
|x|>c (c>0) -c
型如| f(x)|
整体换元的思想,
不等式的性质
课堂延伸:解下列不等式课后作业: 优化方案P16-探究点1同学们再见!
