不等式的基本性质和证明的基本方法(18张)
文档属性
| 名称 | 不等式的基本性质和证明的基本方法(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 15:03:02 | ||
图片预览





文档简介
(共18张PPT)
例题分析
例题分析
能力提升
小结:
绝对值不等式的综合应用中
讨论去绝对值是最基本方法,
当符合一定条件时,绝对值
的三角不等式简化问题,但
要注意等号成立的条件。
例题分析
例题分析
用分析法证“若A则B”
为了证明命题B为真,
只需证明命题B1为真,从而有…
只需证明命题B2为真,从而有…
……
只需证明命题A为真,而已知A为真,故B必真
例题分析
例题分析
小结:
本章介绍的证明不等式的基本方
法有比较、综合、分析、反证、放缩。证明问题的知识依据主要有不等式的性质、基本不等式、绝对值的三角不等式等。
课堂演练
解题过程
巩固练习
解题过程
巩固练习
解题过程
谢谢!
例1解下列关于x的不等式
(1)x-1<3
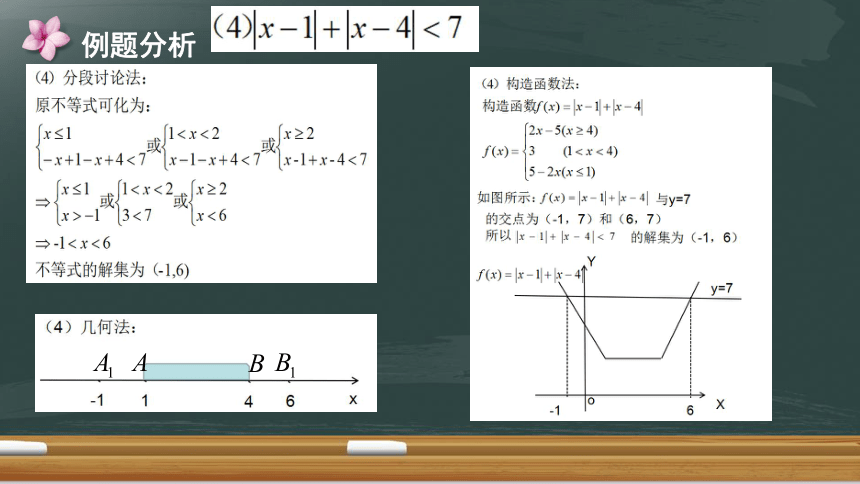
(2)2x-4(3)x-1(4)1x-1+x-41<7
(5)3x+3+x-2>4
(4)构造函数法:
构造函数(x)=x-1+x-4
2x-5(x>4)
f(x)=13(15-2x(x≤1)
如图所示:f(x)=x-1+x-4与y=
7
的交点为(-1,7)和(6,7)
所以|x-1|1+|x-4|<7的解集为(-1,6)
f(x)=1x-1+x-41
y=7
6
(4)分段讨论法:
原不等式可化为:
x<1
x≥2
或
或
x+1-x+4<7|x-1-x+4<7|x-1+x-4<7
{xs1或1x<2或x2
x>-13<7
→-1不等式的解集为(-1,6)
(4)几何法
46
(4)x-1+x-4<7
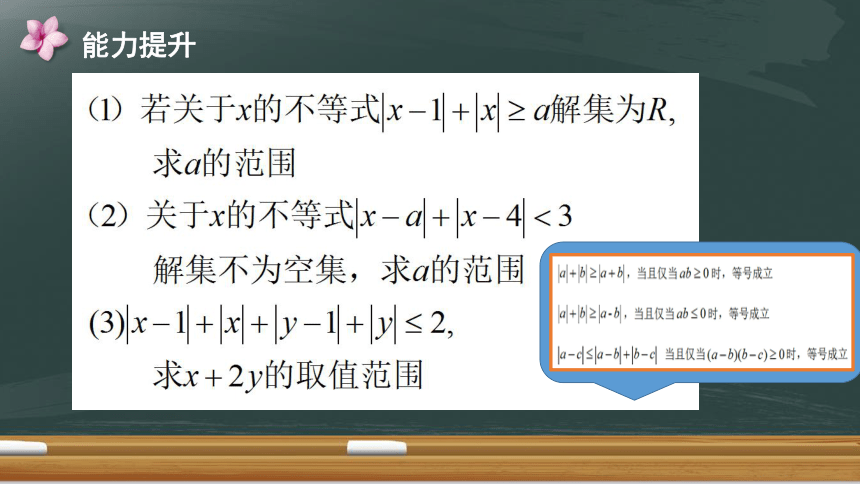
(1)若关于x的不等式x-1+x2a解集为R
求a的范围
(2)关于x的不等式x-a+x-4<3
解集不为空集,求a的范围
(3)x-1+x+|y-1+y≤
求x+2y的取值范围
a+1b≥a+b,当且仅当ab≥0时,等号成立
al+b≥a-b,当且仅当ab≤0时,等号成立
a-s|a-b+b-4当且仅当(a-b)(b-c)≥0时,等号成立
例2证明不等式
(1)求证:a2+b2+1≥ab+a+b
(2)若a>0,b>0,2c>a+b,求证:c2>ab
(3)求证:x-a+x-b2≥a-b
(1)证明
a2+b2+1≥ab+a+b
←2(a2+b2+1)≥2(ab+a+b)
2(a2+b2+1)-2(ab+a+b)≥0
←(a-b)2+(a-1)2+(b-1)2≥0
(1)求证:a2+b2+12ab+a+b
(2)证明:
因为a>0,b>0,2c>a+b
atb
于是c>
atb
atb
又因为
≥ab
所以c2>ab
(2)若a>0,b>0,2c>a+b,求证:c2>ab
(3)证明:由绝对值的三角不等式
a+≥a-b可得
x-a+x-b2(x-a)-(x-b)=a-b
(3)求证:x-a+x-b≥a-b
(2017全国卷I)已知函数f(x)=-x2+ax+4,g(x)=|x+1|+-1
(1)当a=1时,求不等式fx)≥g(x)的解集
(2)若不等式f(x)≥g(x)的解集包含[—1,1],求a的取值范围
解:(1)当a=1时,不等式∫(x)≥g(x)等价于
2-x+x+1+x-1|-4≤0.①
当x<-1时,①式化为x2-3x-4≤0,无解;
当1≤x≤1时,①式化为x2-x-2≤0,从而一1≤x≤1
当x>1时,①式化为x2+x-4≤0,
从而1<-1+17
2
≤x≤=1+7
所以f(x)=g(x)的解集为x
2
(2)当x∈[1,1时,g(x)=2
所以f(x)≥g(x)的解集包含[一1,1,等价于当x∈[1,1]时,f(x)≥2
又f(x)在[1们的最小值必为f(-1)与f(1)之一,
所以f(1)≥2且f(1)≥2,得-1≤a≤1.
已知函数f(x)=2x-a+a
(1)当a=2时,求不等式fx)≤6的解集;
(2)设函数g(x)=2x-1,当x∈R时,fx)+
g(x)≥3,求a的取值范围
解:(1)当a=2时,fx)=2x-2|+
解不等式2x-2+2≤6,得-1≤x≤3
因此,f(x)≤6的解集为{x-1≤x≤3}
(2)当x∈R时,f(x)+gx)=2x-a+a+1-2x≥2x-a+1-2x|+a=1-al+a,
当x=时等号成立,
所以当x∈R时,fx)+g(x)≥3等价于1-a+a≥3
a≤1时,①等价于1-a+a≥3,无解
a>1时,①等价于a-1+a≥3,解得a≥2
所以a的取值范围是[2,+∞)
(1)已知-1<,b-2,求证:|2x+y-4
(2)当一1(1)证明:由(1)知,当a,b∈M时,-1从而(a+b)2-(1+ab)2=a2+b2-a2b2-1=(a2-1)(1-b2)<0,
因此a+b<1+ab
(2)证明:因为x-1,-2
所以2x+y-4=2(x-1)+(y-2)
2|x-1+y-2|<2×+g
课堂小结
例题分析
例题分析
能力提升
小结:
绝对值不等式的综合应用中
讨论去绝对值是最基本方法,
当符合一定条件时,绝对值
的三角不等式简化问题,但
要注意等号成立的条件。
例题分析
例题分析
用分析法证“若A则B”
为了证明命题B为真,
只需证明命题B1为真,从而有…
只需证明命题B2为真,从而有…
……
只需证明命题A为真,而已知A为真,故B必真
例题分析
例题分析
小结:
本章介绍的证明不等式的基本方
法有比较、综合、分析、反证、放缩。证明问题的知识依据主要有不等式的性质、基本不等式、绝对值的三角不等式等。
课堂演练
解题过程
巩固练习
解题过程
巩固练习
解题过程
谢谢!
例1解下列关于x的不等式
(1)x-1<3
(2)2x-4
(5)3x+3+x-2>4
(4)构造函数法:
构造函数(x)=x-1+x-4
2x-5(x>4)
f(x)=13(1
如图所示:f(x)=x-1+x-4与y=
7
的交点为(-1,7)和(6,7)
所以|x-1|1+|x-4|<7的解集为(-1,6)
f(x)=1x-1+x-41
y=7
6
(4)分段讨论法:
原不等式可化为:
x<1
或
或
x+1-x+4<7|x-1-x+4<7|x-1+x-4<7
{xs1或1x<2或x2
x>-13<7
→-1
(4)几何法
46
(4)x-1+x-4<7
(1)若关于x的不等式x-1+x2a解集为R
求a的范围
(2)关于x的不等式x-a+x-4<3
解集不为空集,求a的范围
(3)x-1+x+|y-1+y≤
求x+2y的取值范围
a+1b≥a+b,当且仅当ab≥0时,等号成立
al+b≥a-b,当且仅当ab≤0时,等号成立
a-s|a-b+b-4当且仅当(a-b)(b-c)≥0时,等号成立
例2证明不等式
(1)求证:a2+b2+1≥ab+a+b
(2)若a>0,b>0,2c>a+b,求证:c2>ab
(3)求证:x-a+x-b2≥a-b
(1)证明
a2+b2+1≥ab+a+b
←2(a2+b2+1)≥2(ab+a+b)
2(a2+b2+1)-2(ab+a+b)≥0
←(a-b)2+(a-1)2+(b-1)2≥0
(1)求证:a2+b2+12ab+a+b
(2)证明:
因为a>0,b>0,2c>a+b
atb
于是c>
atb
atb
又因为
≥ab
所以c2>ab
(2)若a>0,b>0,2c>a+b,求证:c2>ab
(3)证明:由绝对值的三角不等式
a+≥a-b可得
x-a+x-b2(x-a)-(x-b)=a-b
(3)求证:x-a+x-b≥a-b
(2017全国卷I)已知函数f(x)=-x2+ax+4,g(x)=|x+1|+-1
(1)当a=1时,求不等式fx)≥g(x)的解集
(2)若不等式f(x)≥g(x)的解集包含[—1,1],求a的取值范围
解:(1)当a=1时,不等式∫(x)≥g(x)等价于
2-x+x+1+x-1|-4≤0.①
当x<-1时,①式化为x2-3x-4≤0,无解;
当1≤x≤1时,①式化为x2-x-2≤0,从而一1≤x≤1
当x>1时,①式化为x2+x-4≤0,
从而1<-1+17
2
≤x≤=1+7
所以f(x)=g(x)的解集为x
2
(2)当x∈[1,1时,g(x)=2
所以f(x)≥g(x)的解集包含[一1,1,等价于当x∈[1,1]时,f(x)≥2
又f(x)在[1们的最小值必为f(-1)与f(1)之一,
所以f(1)≥2且f(1)≥2,得-1≤a≤1.
已知函数f(x)=2x-a+a
(1)当a=2时,求不等式fx)≤6的解集;
(2)设函数g(x)=2x-1,当x∈R时,fx)+
g(x)≥3,求a的取值范围
解:(1)当a=2时,fx)=2x-2|+
解不等式2x-2+2≤6,得-1≤x≤3
因此,f(x)≤6的解集为{x-1≤x≤3}
(2)当x∈R时,f(x)+gx)=2x-a+a+1-2x≥2x-a+1-2x|+a=1-al+a,
当x=时等号成立,
所以当x∈R时,fx)+g(x)≥3等价于1-a+a≥3
a≤1时,①等价于1-a+a≥3,无解
a>1时,①等价于a-1+a≥3,解得a≥2
所以a的取值范围是[2,+∞)
(1)已知-1<,b-2,求证:|2x+y-4
(2)当一1
因此a+b<1+ab
(2)证明:因为x-1,-2
所以2x+y-4=2(x-1)+(y-2)
2|x-1+y-2|<2×+g
课堂小结
