1.3.2 _x-a_+_x-b_≥c,_x-a_+_x-b_≤c型不等式的解法 课件(21张PPT)
文档属性
| 名称 | 1.3.2 _x-a_+_x-b_≥c,_x-a_+_x-b_≤c型不等式的解法 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 13.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 14:58:59 | ||
图片预览








文档简介
课件21张PPT。绝对值不等式的解法4
|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法
① 利用“零点分段法”求解,体现了分类讨论的思想;
② 通过构造函数,利用函数的图象求解,体现了函数与方程的思想.
③ 利用绝对值不等式的几何意义求解,体现了数形结合的思想;方法一:利用零点分段法求解 . 解析:① 当x<-3时,
原不等式化为-(x+3)-(1-2x)< +1,
解得x<10,∴x<-3 .② 当-3≤x< 时,
原不等式化为(x+3)-(1-2x)< +1,
解得x<- ,∴-3≤x<- .③ 当x≥ 时,
原不等式化为(x+3)-(2x-1)< +1,
解得x>2,∴x>2 .解不等式|x+1|+|x-1|≥3 .分析:本题可以用分段讨论法或数形结合法求解.
对于形如|x+a|+|x+b|的代数式,可以认为是分段函数.方法一:利用零点分段法求解 .
当x≤-1时,原不等式可以化为-(x+1)-(x-1)≥3
解得:x≤- .
当-1 即2≥3 . 不成立,无解.
当x≥1时,原不等式可以化为x+1+x-1≥3 .
所以x≥ .
综上,可知原不等式的解集为?方法二:通过构造函数,利用函数的图象求解
将原不等式转化为|x+1|+|x-1|-3≥0 .
构造函数y=|x+1|+|x-1|-3,
即y=
作出函数的图象(如右图).函数的零点是- , .
从图象可知,当x≤- 或x≥ 时,y≥0,
即|x+1|+|x-1|-3≥0 .
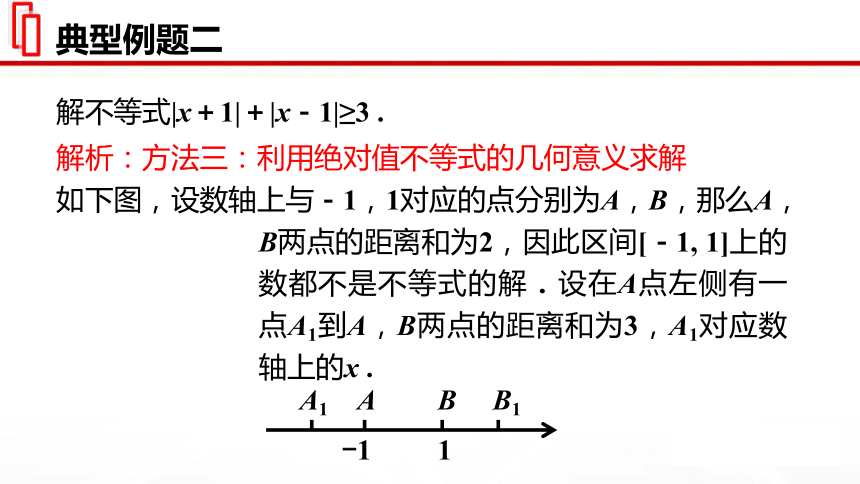
所以原不等式的解集为 .解不等式|x+1|+|x-1|≥3 .解析:方法三:利用绝对值不等式的几何意义求解
如下图,设数轴上与-1,1对应的点分别为A,B,那么A,B两点的距离和为2,因此区间[-1, 1]上的数都不是不等式的解.设在A点左侧有一点A1到A,B两点的距离和为3,A1对应数轴上的x .∴-1-x+1-x=3,得x=- ,
同理设B点右侧有一点B1到A,B两点距离和为3,B1对应数轴上的x,
∴x-1+x-(-1)=3 . ∴x= .
从数轴上可看到,点A1,B1之间的点到A,B的距离之和都小于3;点A1的左边或点B1的右边的任何点到A,B的距离之和都大于3 .
∴原不等式的解集是 .解不等式|x-1|+|x-2|>5 .解析:方法一:利用零点分段法求解
分类讨论|x-1|=0 . |x-2|=0的根1, 2把数轴分成三个区间.在这三个区间上,根据绝对值的定义.代数式|x-1|+|x-2|有不同的解析表达式,因而原不等式的解集为以下三个不等式组解集的并集.(1) 因为在x≤1的限制条件之下:
|x-1|+|x-2|=1-x+2-x=3-2x,
所以当x≤1时,
|x-1|+|x-2|>5?3-2x>5?2x<-2?x<-1 .
因此不等式组 的解集为(-∞,-1).
(2)因为在1 |x-1|+|x-2|=x-1+2-x=1 .
所以当15无解.
因此不等式组 的解集为 ? .(3)由于在x≥2的限制条件之下:
|x-1|+|x-2|=x-1+x-2=2x-3,
所以当x≥2时,|x-1|+|x-2|>5?2x-3>5?2x>8?x>4 .
所以不等式组 的解集为(4,+∞).
于是原不等式的解集为以上三个不等式组解集的并集,
即(-∞,-1)∪?∪(4, +∞)=(-∞, -1)∪(4, +∞).方法二:通过构造函数,利用函数的图象求解
|x-1|+|x-2|>5?|x-1|+|x-2|-5>0 .
构造函数f(x)=|x-1|+|x-2|-5,
于是原不等式的解集为{x|f(x)>0}.
写出f(x)的分段解析表达式:
f(x)=
作出函数f(x)的图象如下图所示.f(x)为分段函数,其零点为-1,4,于是f(x)>0?x<-1或x>4 .
所以原不等式的解集为(-∞,-1)∪(4,+∞).方法三:利用绝对值不等式的几何意义求解
x为不等式|x-1|+|x-2|>5的解集?x是与数轴的点A(1)及B(2)两点距离之和大于5的点.由于A、B两点的距离1,线段AB上的点不符合要求,利用图形(如上图),可知符合条件的点应该是在A点的左侧离A最近距离是2,在B点的右侧离B最近距离为2的点处,即x>4或x<-1,所以原不等式的解集为(-∞,-1)∪(4,+∞).不等式|x-2|+|x-1|≥5的解集是____________________.{x|x≥4 或 x≤-1}解析:方法一:利用零点分段法求解
当x≤1时,原不等式可以化为-(x - 2)-(x-1)≥5,
解得x≤-1.
当1 即1≥5 . 不成立,无解.
当x≥2时,原不等式可以化为(x-2)+(x-1)≥5 .
所以x≥4 .
综上,可知原不等式的解集为{x|x≤-1 或x≥4} .
不等式|x|+|x+1|<2的解集是______________.解析:方法一:利用零点分段法求解
当x≤-1时,原不等式可以化为-x - (x+1)<2,
解得 .
当-1 即1<2 . 成立.
当x≥0时,原不等式可以化为x+(x+1)<2 .
所以 .
综上,可知原不等式的解集为{x| } .形如|x-a|+|x-b|≥c (或≤c) 型的不等式主要有三种解法:
(1)分段讨论法:利用零点分段法求解
利用绝对值号内式子对应方程的根,将数轴分为(-∞, a],(a, b],(b,+∞) (处设a(2)图象法:通过构造函数,利用函数的图象求解
作出函数y1=|x-a|+|x-b|和y2=c的图象,结合图象求解
(3)几何法:利用绝对值不等式的几何意义求解
利用|x-a|+|x-b|>c (c>0) 的几何意义:数轴上到点x1=a和x2=b的距离之和大于c的全体,|x-a|+|x-b|≥|x-a-(x-b)|=|a-b|.
The end
谢谢大家
|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法
① 利用“零点分段法”求解,体现了分类讨论的思想;
② 通过构造函数,利用函数的图象求解,体现了函数与方程的思想.
③ 利用绝对值不等式的几何意义求解,体现了数形结合的思想;方法一:利用零点分段法求解 . 解析:① 当x<-3时,
原不等式化为-(x+3)-(1-2x)< +1,
解得x<10,∴x<-3 .② 当-3≤x< 时,
原不等式化为(x+3)-(1-2x)< +1,
解得x<- ,∴-3≤x<- .③ 当x≥ 时,
原不等式化为(x+3)-(2x-1)< +1,
解得x>2,∴x>2 .解不等式|x+1|+|x-1|≥3 .分析:本题可以用分段讨论法或数形结合法求解.
对于形如|x+a|+|x+b|的代数式,可以认为是分段函数.方法一:利用零点分段法求解 .
当x≤-1时,原不等式可以化为-(x+1)-(x-1)≥3
解得:x≤- .
当-1
当x≥1时,原不等式可以化为x+1+x-1≥3 .
所以x≥ .
综上,可知原不等式的解集为?方法二:通过构造函数,利用函数的图象求解
将原不等式转化为|x+1|+|x-1|-3≥0 .
构造函数y=|x+1|+|x-1|-3,
即y=
作出函数的图象(如右图).函数的零点是- , .
从图象可知,当x≤- 或x≥ 时,y≥0,
即|x+1|+|x-1|-3≥0 .
所以原不等式的解集为 .解不等式|x+1|+|x-1|≥3 .解析:方法三:利用绝对值不等式的几何意义求解
如下图,设数轴上与-1,1对应的点分别为A,B,那么A,B两点的距离和为2,因此区间[-1, 1]上的数都不是不等式的解.设在A点左侧有一点A1到A,B两点的距离和为3,A1对应数轴上的x .∴-1-x+1-x=3,得x=- ,
同理设B点右侧有一点B1到A,B两点距离和为3,B1对应数轴上的x,
∴x-1+x-(-1)=3 . ∴x= .
从数轴上可看到,点A1,B1之间的点到A,B的距离之和都小于3;点A1的左边或点B1的右边的任何点到A,B的距离之和都大于3 .
∴原不等式的解集是 .解不等式|x-1|+|x-2|>5 .解析:方法一:利用零点分段法求解
分类讨论|x-1|=0 . |x-2|=0的根1, 2把数轴分成三个区间.在这三个区间上,根据绝对值的定义.代数式|x-1|+|x-2|有不同的解析表达式,因而原不等式的解集为以下三个不等式组解集的并集.(1) 因为在x≤1的限制条件之下:
|x-1|+|x-2|=1-x+2-x=3-2x,
所以当x≤1时,
|x-1|+|x-2|>5?3-2x>5?2x<-2?x<-1 .
因此不等式组 的解集为(-∞,-1).
(2)因为在1
所以当1
因此不等式组 的解集为 ? .(3)由于在x≥2的限制条件之下:
|x-1|+|x-2|=x-1+x-2=2x-3,
所以当x≥2时,|x-1|+|x-2|>5?2x-3>5?2x>8?x>4 .
所以不等式组 的解集为(4,+∞).
于是原不等式的解集为以上三个不等式组解集的并集,
即(-∞,-1)∪?∪(4, +∞)=(-∞, -1)∪(4, +∞).方法二:通过构造函数,利用函数的图象求解
|x-1|+|x-2|>5?|x-1|+|x-2|-5>0 .
构造函数f(x)=|x-1|+|x-2|-5,
于是原不等式的解集为{x|f(x)>0}.
写出f(x)的分段解析表达式:
f(x)=
作出函数f(x)的图象如下图所示.f(x)为分段函数,其零点为-1,4,于是f(x)>0?x<-1或x>4 .
所以原不等式的解集为(-∞,-1)∪(4,+∞).方法三:利用绝对值不等式的几何意义求解
x为不等式|x-1|+|x-2|>5的解集?x是与数轴的点A(1)及B(2)两点距离之和大于5的点.由于A、B两点的距离1,线段AB上的点不符合要求,利用图形(如上图),可知符合条件的点应该是在A点的左侧离A最近距离是2,在B点的右侧离B最近距离为2的点处,即x>4或x<-1,所以原不等式的解集为(-∞,-1)∪(4,+∞).不等式|x-2|+|x-1|≥5的解集是____________________.{x|x≥4 或 x≤-1}解析:方法一:利用零点分段法求解
当x≤1时,原不等式可以化为-(x - 2)-(x-1)≥5,
解得x≤-1.
当1
当x≥2时,原不等式可以化为(x-2)+(x-1)≥5 .
所以x≥4 .
综上,可知原不等式的解集为{x|x≤-1 或x≥4} .
不等式|x|+|x+1|<2的解集是______________.解析:方法一:利用零点分段法求解
当x≤-1时,原不等式可以化为-x - (x+1)<2,
解得 .
当-1
当x≥0时,原不等式可以化为x+(x+1)<2 .
所以 .
综上,可知原不等式的解集为{x| } .形如|x-a|+|x-b|≥c (或≤c) 型的不等式主要有三种解法:
(1)分段讨论法:利用零点分段法求解
利用绝对值号内式子对应方程的根,将数轴分为(-∞, a],(a, b],(b,+∞) (处设a
作出函数y1=|x-a|+|x-b|和y2=c的图象,结合图象求解
(3)几何法:利用绝对值不等式的几何意义求解
利用|x-a|+|x-b|>c (c>0) 的几何意义:数轴上到点x1=a和x2=b的距离之和大于c的全体,|x-a|+|x-b|≥|x-a-(x-b)|=|a-b|.
The end
谢谢大家
