2.1.1 平面上的柯西不等式的代数和向量形式 课件(23张PPT)
文档属性
| 名称 | 2.1.1 平面上的柯西不等式的代数和向量形式 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览







文档简介
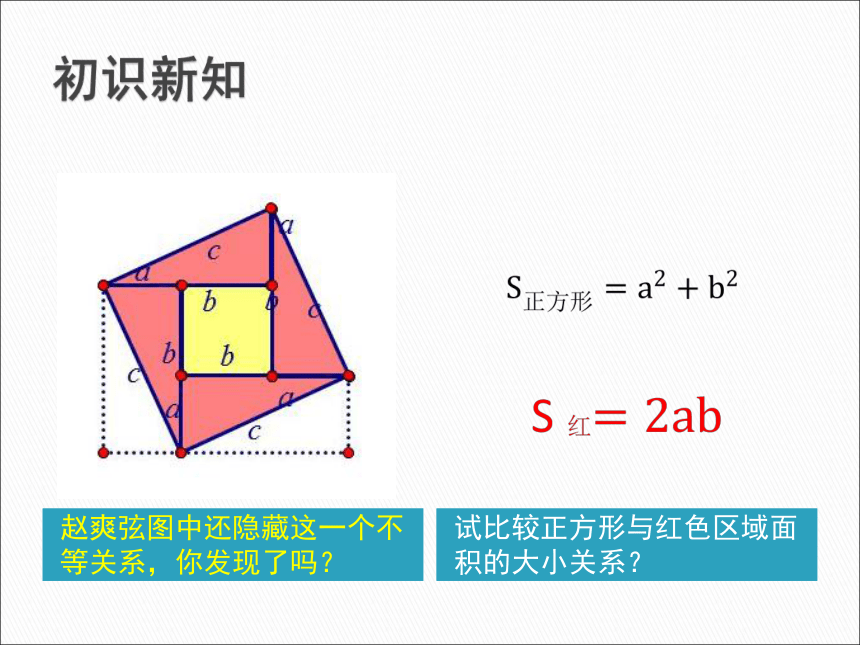
课件23张PPT。赵爽弦图2002年数学家大会会徽赵爽弦图这一设计的基础是公元3世纪中国数学家赵爽的弦图,是为证明发明于周代的勾股定理而绘制的.初识新知赵爽弦图中还隐藏这一个不等关系,你发现了吗?试比较正方形与红色区域面积的大小关系?&2.1.1平面上的柯西不等式的代数和向量形式人教B版 选修4-5不等式选讲柯西小传
柯西画像
柯西的主要贡献柯西(Cauchy),法国人,生于1789年8月21日,卒于1857年5月23日,是十九世纪前半叶最杰出的分析家. 他奠定了数学分析的理论基础,重要贡献在微积分、复变函数和微分方程等方面. 数学中很多定理都冠以柯西的名字,如柯西收敛原理、柯西中值定理、柯西积分不等式、柯西判别法、柯西方程等等.一生共出版7部著作和800多篇论文.
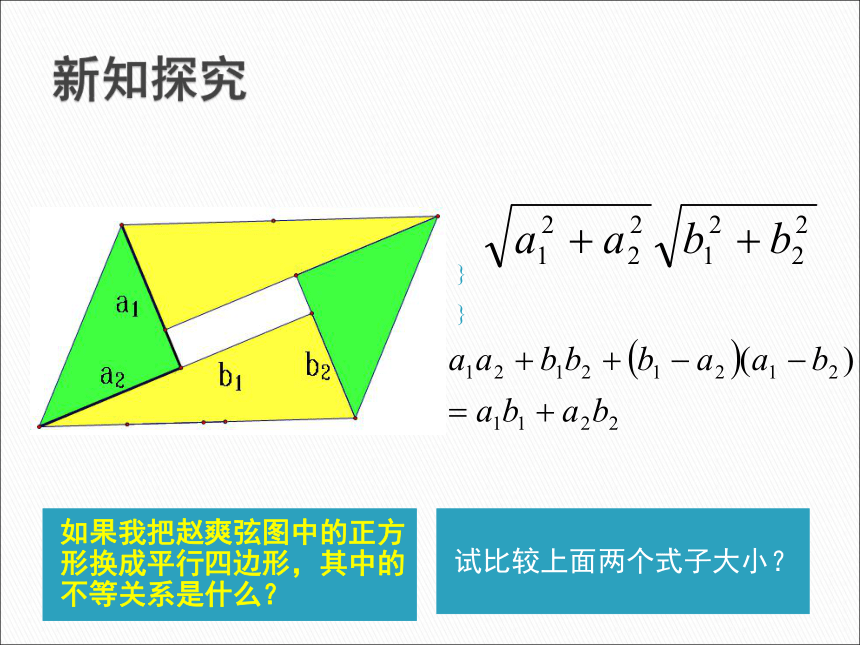
柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。但从历史的角度讲,该不等式应当称为Cauchy-Buniakowsky-Schwarz不等式【柯西-布尼亚科夫斯基-施瓦茨不等式】,因为,正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式应用到近乎完善的地步。柯西不等式新知探究如果我把赵爽弦图中的正方形换成平行四边形,其中的不等关系是什么?试比较上面两个式子大小?
?
?
若a1,a2,b1,b2都是实数,则
(a12+a22)(b12+b22)≥(a1b1+a2b2)2
当且仅当a1b2=a2b1时,等号成立.
定理1(柯西不等式的代数形式) 变形:(a12+a22)(b12+b22)≥(a1b1+a2b2)2定理2: (柯西不等式的向量形式) 设α,β是平面上的两个向量定理3(柯西不等式的三角形式)定理4(平面三角不等式)定理5在探究柯西不等式的过程中,你的收获是什么?探究小结走进柯西应用柯西---不等式证明应用柯西---求函数最值你们的小结知识层面
技能层面
情感价值观
数学思想
数学之美来龙去脉摸清楚,向量关系是基础;
结构特征要牢记,比较结构有思路;
化和为积巧分离,化积为和细设计;
不等变换做传递,相等条件列等式.
我的小结你的眼光决定了世界的色彩看法不一样,形式就不一样
柯西画像
柯西的主要贡献柯西(Cauchy),法国人,生于1789年8月21日,卒于1857年5月23日,是十九世纪前半叶最杰出的分析家. 他奠定了数学分析的理论基础,重要贡献在微积分、复变函数和微分方程等方面. 数学中很多定理都冠以柯西的名字,如柯西收敛原理、柯西中值定理、柯西积分不等式、柯西判别法、柯西方程等等.一生共出版7部著作和800多篇论文.
柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。但从历史的角度讲,该不等式应当称为Cauchy-Buniakowsky-Schwarz不等式【柯西-布尼亚科夫斯基-施瓦茨不等式】,因为,正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式应用到近乎完善的地步。柯西不等式新知探究如果我把赵爽弦图中的正方形换成平行四边形,其中的不等关系是什么?试比较上面两个式子大小?
?
?
若a1,a2,b1,b2都是实数,则
(a12+a22)(b12+b22)≥(a1b1+a2b2)2
当且仅当a1b2=a2b1时,等号成立.
定理1(柯西不等式的代数形式) 变形:(a12+a22)(b12+b22)≥(a1b1+a2b2)2定理2: (柯西不等式的向量形式) 设α,β是平面上的两个向量定理3(柯西不等式的三角形式)定理4(平面三角不等式)定理5在探究柯西不等式的过程中,你的收获是什么?探究小结走进柯西应用柯西---不等式证明应用柯西---求函数最值你们的小结知识层面
技能层面
情感价值观
数学思想
数学之美来龙去脉摸清楚,向量关系是基础;
结构特征要牢记,比较结构有思路;
化和为积巧分离,化积为和细设计;
不等变换做传递,相等条件列等式.
我的小结你的眼光决定了世界的色彩看法不一样,形式就不一样
