湘教版八年级数学上册2.1.2三角形的高、角平分线和中线课件(27张ppt)
文档属性
| 名称 | 湘教版八年级数学上册2.1.2三角形的高、角平分线和中线课件(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 22:14:47 | ||
图片预览





文档简介
课件26张PPT。第2章
三角形八年级数学湘教版·上册2.1.2三角形的高、角平分线和中线授课人:XXXX学习目标1.三角形角平分线、中线、高的概念及其画法;(重点)
2.钝角三角形高的画法.(难点)新课导入2.线段中点的定义:3.角的平分线的定义:1.垂线的定义:一条射线把一个角分成两个相等的角,
这条射线叫作这个角的平分线.把一条线段分成两条相等的线段的点.当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫作另一条直线的垂线.新课导入1.三角形的定义: 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫作三角形.2.三角形的分类:锐角三角形
直角三角形
钝角三角形不等边三角形
等腰三角形底边与腰不相等的等腰三角形
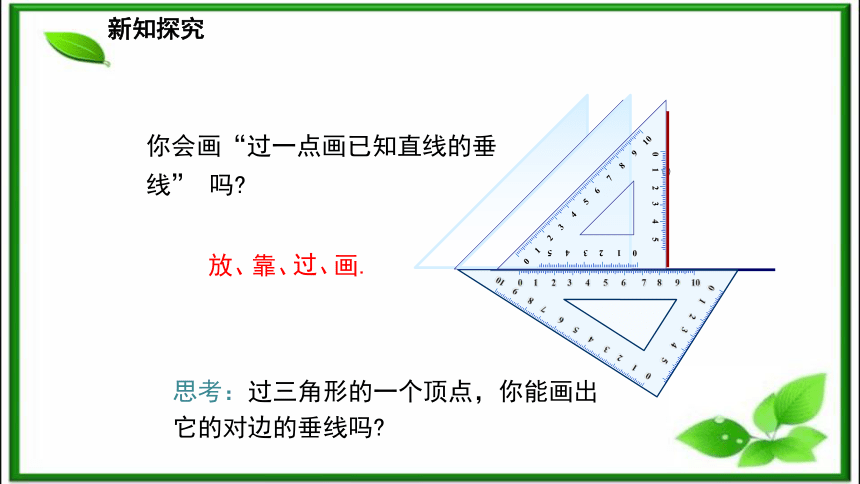
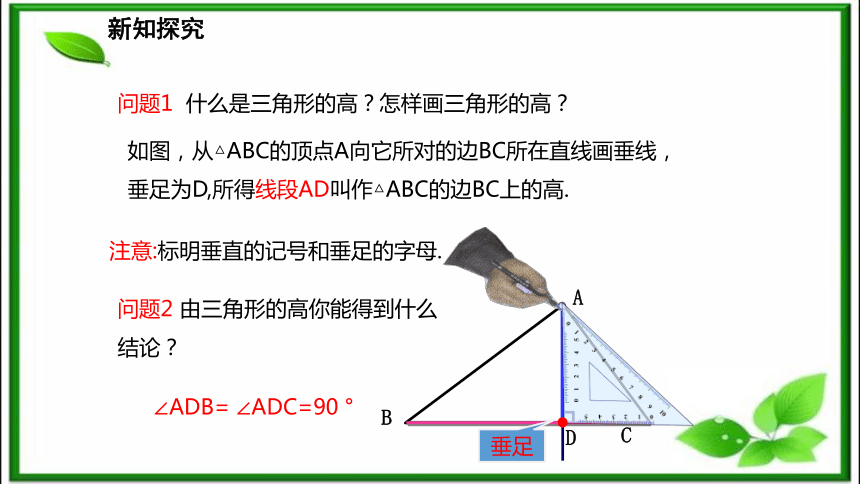
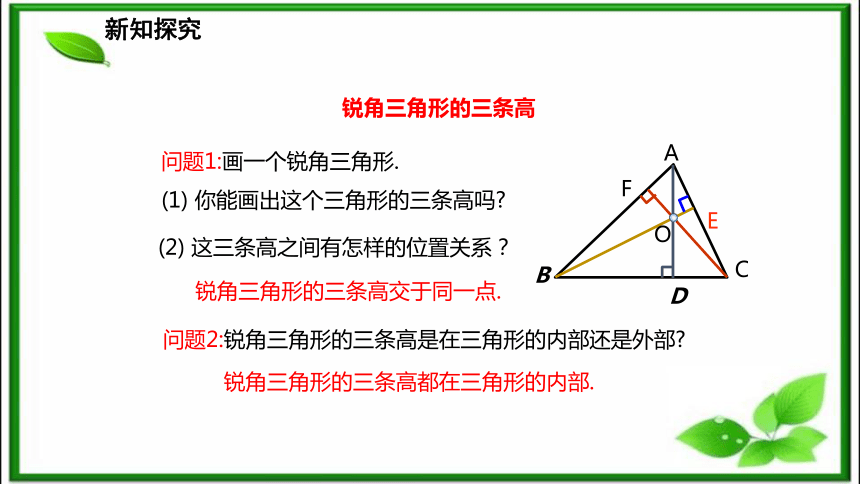
等边三角形3.三角形的三边关系: 三角形任意两边之和大于第三边,任意两边之差小于第三边.按角分 按边分新知探究你会画“过一点画已知直线的垂线” 吗?放、靠、过、画.思考:过三角形的一个顶点,你能画出它的对边的垂线吗?新知探究问题1 什么是三角形的高?怎样画三角形的高?如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫作△ABC的边BC上的高.问题2 由三角形的高你能得到什么结论?∠ADB= ∠ADC=90 °ABC垂足注意:标明垂直的记号和垂足的字母.锐角三角形的三条高问题1:画一个锐角三角形.
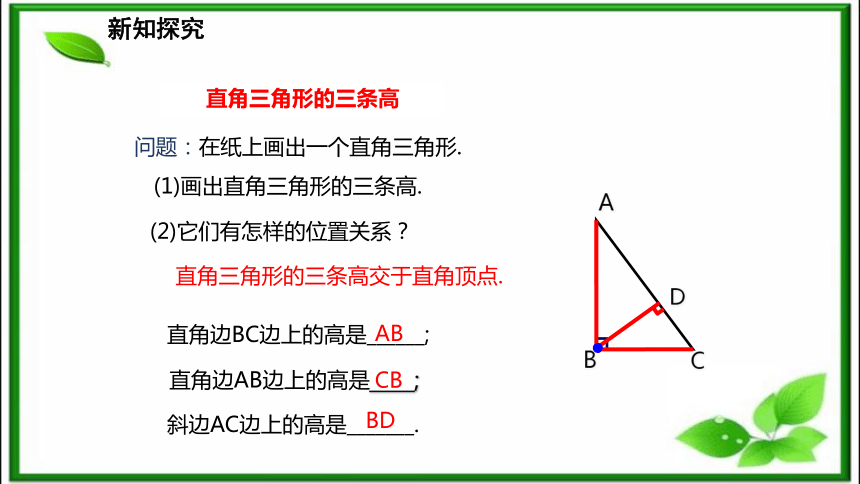
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?问题2:锐角三角形的三条高是在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部.新知探究新知探究直角三角形的三条高问题:在纸上画出一个直角三角形.ABC(1)画出直角三角形的三条高.直角边BC边上的高是______; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是_______. BD●直角三角形的三条高交于直角顶点.新知探究钝角三角形的三条高 (1) 你能画出钝角三角形的三条
高吗?DEFBFCEADABCDF(3)钝角三角形的三条高交于一点吗?(4)它们所在的直线交于一点吗?OE钝角三角形的三条高不相交于一点;钝角三角形的三条高所在的直线交于一点.新知探究从三角形中的一个顶点向它的对边的所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
三角形的三条高所在的直线交于一点.
新知探究三角形的角平分线ABCD∵AD是 ∠ ABC的角平分线●●三角形的角平分线与角的角平分线相同吗?
相同点: ∠ BAD= ∠ CAD;
不同点:前者是线段,后者是射线.新知探究问题4:请画出这个三角形的另外两条角平分线,你发现了什么?三角形的三条角平分线交于一点.ABCDEF问题3:一个三角形有几条角平分线?3称之为三角形的内心.新知探究在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.
三角形的三条角平分线交于一点称之为三角形的内心.
新知探究问题5 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线?ABC如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫作△ABC的边BC上的中线.想一想:由三角形的中线能得到什么结论?BD=CD= BC新知探究画一画:如图,分别画出下列三角形的三条中线,并观察它们中线的交点有什么规律?画图发现 三角形的三条中线相交于一点.我们称为三角形的重心.ABCABCABCDEFDDEFEF问题6 如图所示,在△ABC中,AD是△ABC的中线,AE是
△ABC的高.试判断△ABD和△ACD的面积有什么关系?
为什么?答:相等,因为两个三角形等底同高,所以它们的面积相等.问题7 通过问题6你能发现什么规律?答:三角形的中线能将三角形的面积平分.新知探究新知探究在三角形中,连接一个顶点与它的对边中点的线段叫作三角形的中线.
三角形的三条中线相交于一点,我们称为三角形的重心.新知探究例2 如图,AD是△ABC的中线, AE是△ABC的高.
(1)图中共有几个三角形?请分别列举出来;解: (1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.新知探究(2)其中哪些三角形的面积相等?解: 因为AD是△ABC的中线,所以 BD=DC.因为AE是△ABC的高,也是△ABD和△ADC的高,所以S△ABD = S△ADC .又S△ABD = BD?AE,S△ADC = DC?AE, 新知探究三角形的中线把三角形分成面积相等的两个部分.课堂小结与三角形有关的线段三角形中,连接一个顶点和它对边中点的线段叫作三角形的中线.三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线.(2) 如图所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有的性质是( ) .
A.边BB′上的中线 B.边BB′上的高
C.∠BAB′的平分线 D.以上三种性质合一
(1)下列说法正确的是 ( ).
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线课堂小测1.选择.BD课堂小测2.填空.(1)如图1,AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= .
(2)如图2, AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 . AFCD? ∠2 ?∠4课堂小测3.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高.
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
CEBC∠CAD∠BAC∠AFC4.如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35cm,BC=11cm,且△ABD与△ACD的周长差为3cm,求AB与AC的长.解: ∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
∵△ABD与△ACD的周长差为3cm,
∴AB-AC=3cm,
∴AB=13.5cm,AC=10.5cm.课堂小测课堂小测5.在△ABC中,CD是中线,已知BC-AC=5cm, △DBC的周长为25cm,求ΔADC的周长.解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)
=25-5
=20cm.
2.钝角三角形高的画法.(难点)新课导入2.线段中点的定义:3.角的平分线的定义:1.垂线的定义:一条射线把一个角分成两个相等的角,
这条射线叫作这个角的平分线.把一条线段分成两条相等的线段的点.当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫作另一条直线的垂线.新课导入1.三角形的定义: 由不在同一直线上的三条线段首尾顺次相接所组成的图形叫作三角形.2.三角形的分类:锐角三角形
直角三角形
钝角三角形不等边三角形
等腰三角形底边与腰不相等的等腰三角形
等边三角形3.三角形的三边关系: 三角形任意两边之和大于第三边,任意两边之差小于第三边.按角分 按边分新知探究你会画“过一点画已知直线的垂线” 吗?放、靠、过、画.思考:过三角形的一个顶点,你能画出它的对边的垂线吗?新知探究问题1 什么是三角形的高?怎样画三角形的高?如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫作△ABC的边BC上的高.问题2 由三角形的高你能得到什么结论?∠ADB= ∠ADC=90 °ABC垂足注意:标明垂直的记号和垂足的字母.锐角三角形的三条高问题1:画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?问题2:锐角三角形的三条高是在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部.新知探究新知探究直角三角形的三条高问题:在纸上画出一个直角三角形.ABC(1)画出直角三角形的三条高.直角边BC边上的高是______; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是_______. BD●直角三角形的三条高交于直角顶点.新知探究钝角三角形的三条高 (1) 你能画出钝角三角形的三条
高吗?DEFBFCEADABCDF(3)钝角三角形的三条高交于一点吗?(4)它们所在的直线交于一点吗?OE钝角三角形的三条高不相交于一点;钝角三角形的三条高所在的直线交于一点.新知探究从三角形中的一个顶点向它的对边的所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
三角形的三条高所在的直线交于一点.
新知探究三角形的角平分线ABCD∵AD是 ∠ ABC的角平分线●●三角形的角平分线与角的角平分线相同吗?
相同点: ∠ BAD= ∠ CAD;
不同点:前者是线段,后者是射线.新知探究问题4:请画出这个三角形的另外两条角平分线,你发现了什么?三角形的三条角平分线交于一点.ABCDEF问题3:一个三角形有几条角平分线?3称之为三角形的内心.新知探究在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.
三角形的三条角平分线交于一点称之为三角形的内心.
新知探究问题5 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.类比三角形的高的概念,试说明什么叫三角形的中线?ABC如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫作△ABC的边BC上的中线.想一想:由三角形的中线能得到什么结论?BD=CD= BC新知探究画一画:如图,分别画出下列三角形的三条中线,并观察它们中线的交点有什么规律?画图发现 三角形的三条中线相交于一点.我们称为三角形的重心.ABCABCABCDEFDDEFEF问题6 如图所示,在△ABC中,AD是△ABC的中线,AE是
△ABC的高.试判断△ABD和△ACD的面积有什么关系?
为什么?答:相等,因为两个三角形等底同高,所以它们的面积相等.问题7 通过问题6你能发现什么规律?答:三角形的中线能将三角形的面积平分.新知探究新知探究在三角形中,连接一个顶点与它的对边中点的线段叫作三角形的中线.
三角形的三条中线相交于一点,我们称为三角形的重心.新知探究例2 如图,AD是△ABC的中线, AE是△ABC的高.
(1)图中共有几个三角形?请分别列举出来;解: (1)图中有6个三角形,它们分别是:△ABD,△ADE,△AEC,△ABE,△ADC,△ABC.新知探究(2)其中哪些三角形的面积相等?解: 因为AD是△ABC的中线,所以 BD=DC.因为AE是△ABC的高,也是△ABD和△ADC的高,所以S△ABD = S△ADC .又S△ABD = BD?AE,S△ADC = DC?AE, 新知探究三角形的中线把三角形分成面积相等的两个部分.课堂小结与三角形有关的线段三角形中,连接一个顶点和它对边中点的线段叫作三角形的中线.三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线.(2) 如图所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有的性质是( ) .
A.边BB′上的中线 B.边BB′上的高
C.∠BAB′的平分线 D.以上三种性质合一
(1)下列说法正确的是 ( ).
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线课堂小测1.选择.BD课堂小测2.填空.(1)如图1,AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= .
(2)如图2, AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 . AFCD? ∠2 ?∠4课堂小测3.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高.
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
CEBC∠CAD∠BAC∠AFC4.如图,△ABC中,AD是BC边上的中线,若△ABC的周长为35cm,BC=11cm,且△ABD与△ACD的周长差为3cm,求AB与AC的长.解: ∵AD是△ABC的中线,
∴CD=BD.
∵△ABC的周长为35cm,BC=11cm,
∴AC+AB=35-11=24(cm).
∵△ABD与△ACD的周长差为3cm,
∴AB-AC=3cm,
∴AB=13.5cm,AC=10.5cm.课堂小测课堂小测5.在△ABC中,CD是中线,已知BC-AC=5cm, △DBC的周长为25cm,求ΔADC的周长.解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)
=25-5
=20cm.
同课章节目录
