2.3.1等腰三角形的性质 课件(27张ppt)
文档属性
| 名称 | 2.3.1等腰三角形的性质 课件(27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 396.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 22:14:16 | ||
图片预览




文档简介
课件27张PPT。第2章
三角形八年级数学湘教版·上册2.3.1等腰三角形的性质授课人:XXXX学习目标1.等腰三角形的性质及其应用,等边三角形的性质;(重点)
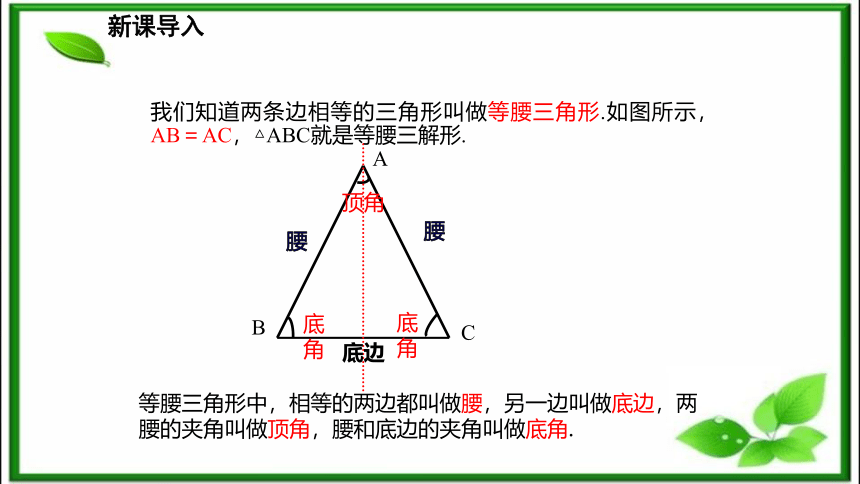
2.能运用等腰(边)三角形的性质进行有关的证明和计算.(难点)腰新课导入我们知道两条边相等的三角形叫做等腰三角形.如图所示,AB=AC,△ABC就是等腰三解形.等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
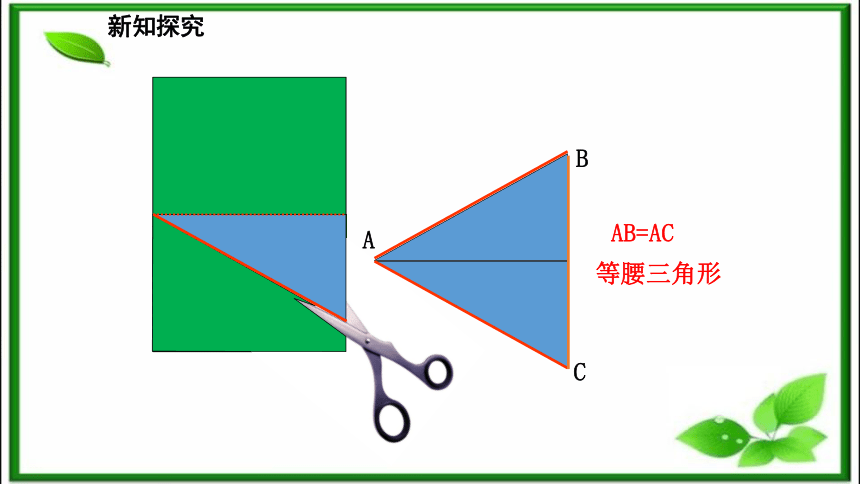
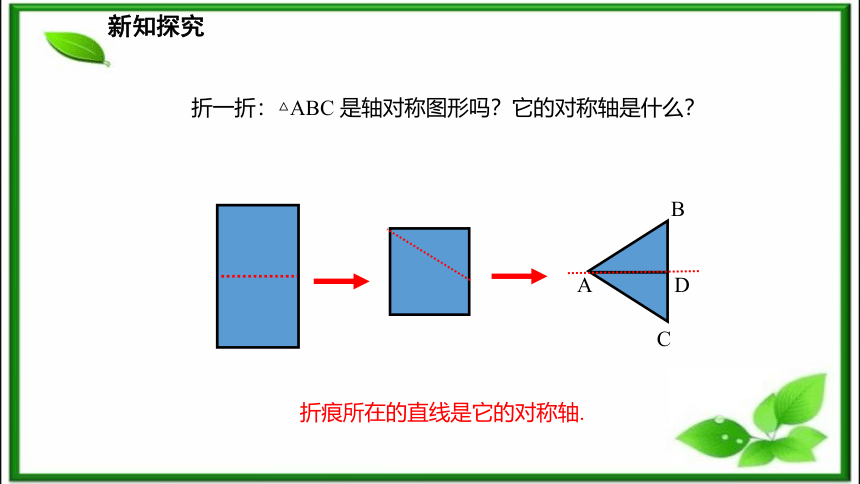
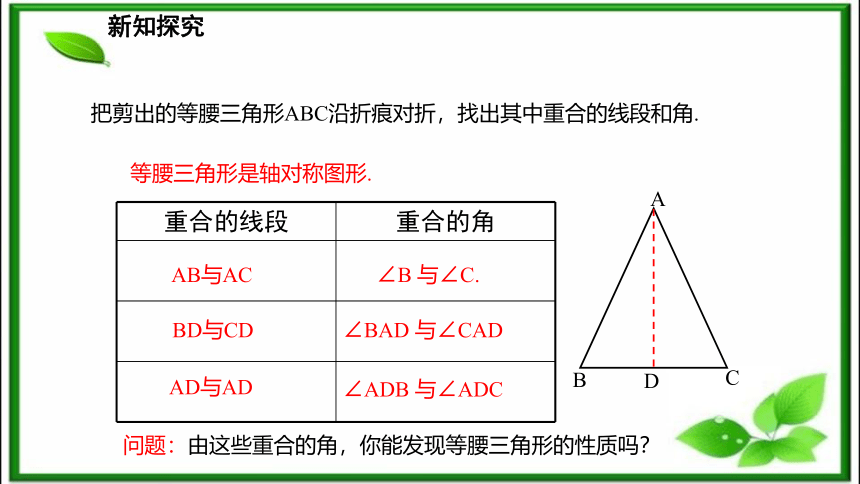
腰CBA顶角底边新知探究剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点?ABCAB=AC等腰三角形新知探究折一折:△ABC 是轴对称图形吗?它的对称轴是什么?折痕所在的直线是它的对称轴.新知探究把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角. AC B D AB与AC BD与CD AD与AD ∠B 与∠C.∠BAD 与∠CAD∠ADB 与∠ADC等腰三角形是轴对称图形.问题:由这些重合的角,你能发现等腰三角形的性质吗?新知探究新知探究等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
等腰三角形的两底角相等(简称“等边对等角”).
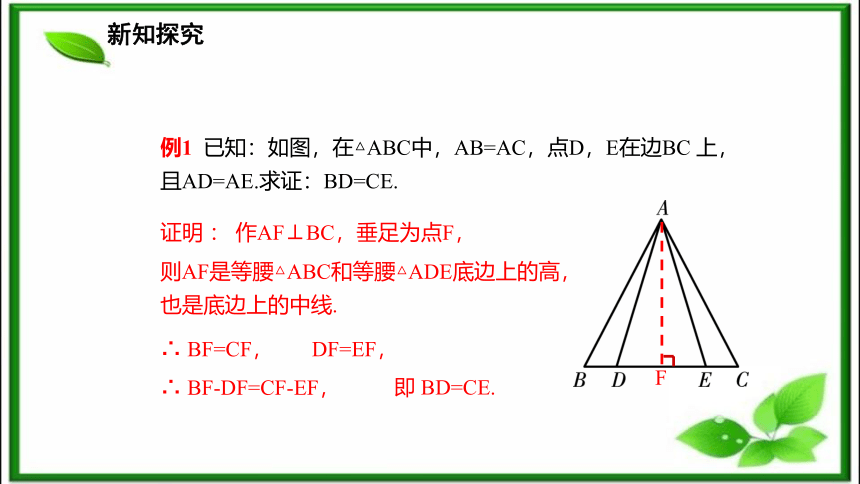
新知探究例1 已知:如图,在△ABC中,AB=AC,点D,E在边BC 上,且AD=AE.求证:BD=CE.证明 : 作AF⊥BC,垂足为点F,则AF是等腰△ABC和等腰△ADE底边上的高,也是底边上的中线.∴ BF=CF,∴ BF-DF=CF-EF,DF=EF,即 BD=CE.新知探究 在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
(2)设∠A=x,请把△ ABC的内角和用含x的式子表示出来. 例2 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.解析:(1)观察∠BDC与∠A,∠ABD的关系,∠ABC,∠C呢?∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,∠ABC= ∠C= ∠BDC=2 ∠A,∠C= ∠BDC=2 ∠A.∵ ∠A+ ∠ABC+ ∠ C=180 °,
∴x+2x+2x=180 °,新知探究解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得 x=36 ° ,
在△ABC中, ∠A=36°,∠ABC=∠C=72°.新知探究新知探究 利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角、直角或者钝角.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.(×)(×)(×)(×)(√)(√)判断题新知探究类比探究等边三角形的三个内角之间有什么关系?等腰三角形AB=AC∠B=∠C等边三角形AB=AC=BCAB=AC∠B=∠CAC=BC∠A=∠B∠A=∠B=∠C=60°内角和为180°新知探究新知探究 如图, △ABC 是等边三角形, 那么∠A, ∠B,∠C 的大小之间有什么关系呢?因为△ABC 是等边三角形,
所以AB=BC=AC,
从而∠C =∠A=∠B.
由三角形内角和定理,得
∠A=∠B=∠C = 60°.新知探究等边三角形的三个内角相等,且都等于60°.
等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?顶角的平分线、底边上的高
底边的中线
三线合一一条对称轴三条对称轴新知探究新知探究 等边三角形每条边上的中线、高和所对角的平分线都“三线合一”.
新知探究例3 等腰三角形的一个内角是50°,求这个三角形的底角的度数.解:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.新知探究例4 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE, ∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.新知探究 等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合”等边对等角”、三角形的内角和与外角的性质.
课堂小结等腰三角形的性质三线合一,注意是指顶角的平分线、底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.等边对等角,注意是指同一个三角形中.推论,等边三角形三个内角相等且均等于60°.课堂小测1. 选择题(2)如图,在△ABC中,AB=AC,过点A作AD∥BC,若 ∠1=70°,
则∠BAC的大小为( )
A.40° B.30° C.70° D.50° A(1)等腰三角形有一个角是90°,则另两个角的度数分别是 ( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70° B课堂小测 (1)等腰三角形一个底角为75°,它的另外两个角为 .
(2)等腰三角形一个角为36°,它的另外两个角为 .
(3)等腰三角形一个角为120°,它的另外两个角为 .75°, 30°72°,72°或36°,108°30°,30°2. 填空题课堂小测3.如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 30°,求 ∠BAD 和 ∠ADC的度数.解:∵AB=AC,D是BC边上的中点, ∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°. ∴∠ BAC =180° - 30°-30° = 120°.课堂小测课堂小结4. 如图,点P为等边三角形ABC的边BC上一点,且∠APD= 80°,AD=AP,求∠DPC的度数.解:∵三角形ABC是等边三角形,
∴C=60? ,
∵AD=AP,
∴∠APD= ∠ADP =80°,
∴∠DPC= ∠ADP - ∠C
=20?.
2.能运用等腰(边)三角形的性质进行有关的证明和计算.(难点)腰新课导入我们知道两条边相等的三角形叫做等腰三角形.如图所示,AB=AC,△ABC就是等腰三解形.等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
腰CBA顶角底边新知探究剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点?ABCAB=AC等腰三角形新知探究折一折:△ABC 是轴对称图形吗?它的对称轴是什么?折痕所在的直线是它的对称轴.新知探究把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角. AC B D AB与AC BD与CD AD与AD ∠B 与∠C.∠BAD 与∠CAD∠ADB 与∠ADC等腰三角形是轴对称图形.问题:由这些重合的角,你能发现等腰三角形的性质吗?新知探究新知探究等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
等腰三角形的两底角相等(简称“等边对等角”).
新知探究例1 已知:如图,在△ABC中,AB=AC,点D,E在边BC 上,且AD=AE.求证:BD=CE.证明 : 作AF⊥BC,垂足为点F,则AF是等腰△ABC和等腰△ADE底边上的高,也是底边上的中线.∴ BF=CF,∴ BF-DF=CF-EF,DF=EF,即 BD=CE.新知探究 在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
(2)设∠A=x,请把△ ABC的内角和用含x的式子表示出来. 例2 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.解析:(1)观察∠BDC与∠A,∠ABD的关系,∠ABC,∠C呢?∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,∠ABC= ∠C= ∠BDC=2 ∠A,∠C= ∠BDC=2 ∠A.∵ ∠A+ ∠ABC+ ∠ C=180 °,
∴x+2x+2x=180 °,新知探究解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得 x=36 ° ,
在△ABC中, ∠A=36°,∠ABC=∠C=72°.新知探究新知探究 利用等腰三角形的性质和三角形外角的性质可以得到角与角之间的关系,当这种等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角、直角或者钝角.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.(×)(×)(×)(×)(√)(√)判断题新知探究类比探究等边三角形的三个内角之间有什么关系?等腰三角形AB=AC∠B=∠C等边三角形AB=AC=BCAB=AC∠B=∠CAC=BC∠A=∠B∠A=∠B=∠C=60°内角和为180°新知探究新知探究 如图, △ABC 是等边三角形, 那么∠A, ∠B,∠C 的大小之间有什么关系呢?因为△ABC 是等边三角形,
所以AB=BC=AC,
从而∠C =∠A=∠B.
由三角形内角和定理,得
∠A=∠B=∠C = 60°.新知探究等边三角形的三个内角相等,且都等于60°.
等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?顶角的平分线、底边上的高
底边的中线
三线合一一条对称轴三条对称轴新知探究新知探究 等边三角形每条边上的中线、高和所对角的平分线都“三线合一”.
新知探究例3 等腰三角形的一个内角是50°,求这个三角形的底角的度数.解:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.方法总结:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.新知探究例4 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE, ∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.新知探究 等边三角形是特殊的三角形,它的三个内角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合”等边对等角”、三角形的内角和与外角的性质.
课堂小结等腰三角形的性质三线合一,注意是指顶角的平分线、底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.等边对等角,注意是指同一个三角形中.推论,等边三角形三个内角相等且均等于60°.课堂小测1. 选择题(2)如图,在△ABC中,AB=AC,过点A作AD∥BC,若 ∠1=70°,
则∠BAC的大小为( )
A.40° B.30° C.70° D.50° A(1)等腰三角形有一个角是90°,则另两个角的度数分别是 ( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70° B课堂小测 (1)等腰三角形一个底角为75°,它的另外两个角为 .
(2)等腰三角形一个角为36°,它的另外两个角为 .
(3)等腰三角形一个角为120°,它的另外两个角为 .75°, 30°72°,72°或36°,108°30°,30°2. 填空题课堂小测3.如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 30°,求 ∠BAD 和 ∠ADC的度数.解:∵AB=AC,D是BC边上的中点, ∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°. ∴∠ BAC =180° - 30°-30° = 120°.课堂小测课堂小结4. 如图,点P为等边三角形ABC的边BC上一点,且∠APD= 80°,AD=AP,求∠DPC的度数.解:∵三角形ABC是等边三角形,
∴C=60? ,
∵AD=AP,
∴∠APD= ∠ADP =80°,
∴∠DPC= ∠ADP - ∠C
=20?.
同课章节目录
