2.3.2等腰三角形的判定 课件(22张ppt)
文档属性
| 名称 | 2.3.2等腰三角形的判定 课件(22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 255.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-06 09:39:57 | ||
图片预览




文档简介
课件22张PPT。第2章
三角形八年级数学湘教版·上册2.3.2等腰三角形的判定授课人:XXXX学习目标1.掌握等腰三角形和等边三角形的判定定理;(重点)
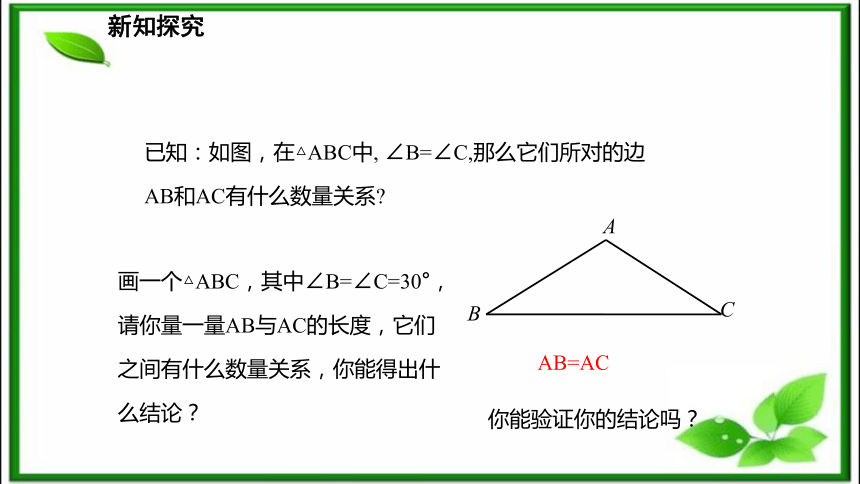
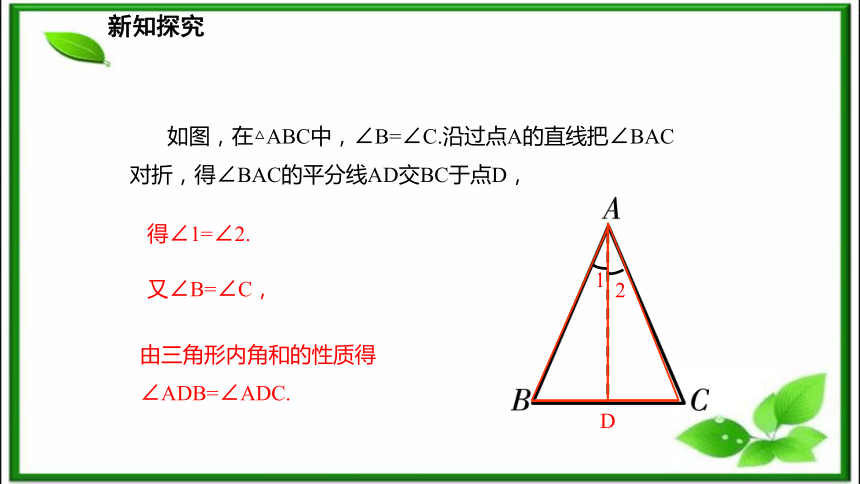
2.掌握等腰三角形和等边三角形的判定定理的运用.(难点)新课导入1、等腰三角形是怎样定义的?有两条边相等的三角形叫作等腰三角形.③等腰三角形是轴对称图形.② 等腰三角形顶角的平分线、底边上的中线、底边上的高重合 (简称“三线合一”).① 等腰三角形的两个底角相等.(简写成“等边对等角”)2、等腰三角形有哪些性质?复习新课导入把“等腰三角形的两个底角相等”改写成“如果------那么-----”的形式.如果一个三角形有两个角相等,那么这个三角形是等腰三角形.如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.新知探究已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?AB=AC你能验证你的结论吗?新知探究 如图,在△ABC中,∠B=∠C.沿过点A的直线把∠BAC对折,得∠BAC的平分线AD交BC于点D,得∠1=∠2.又∠B=∠C,由三角形内角和的性质得
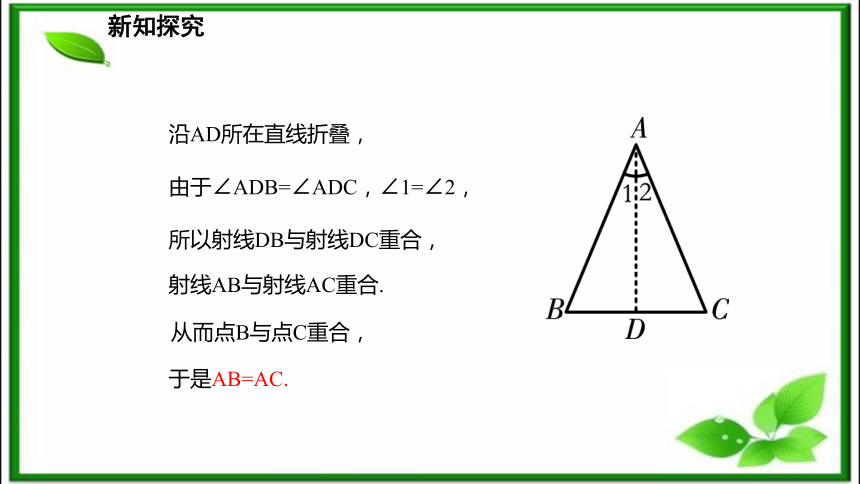
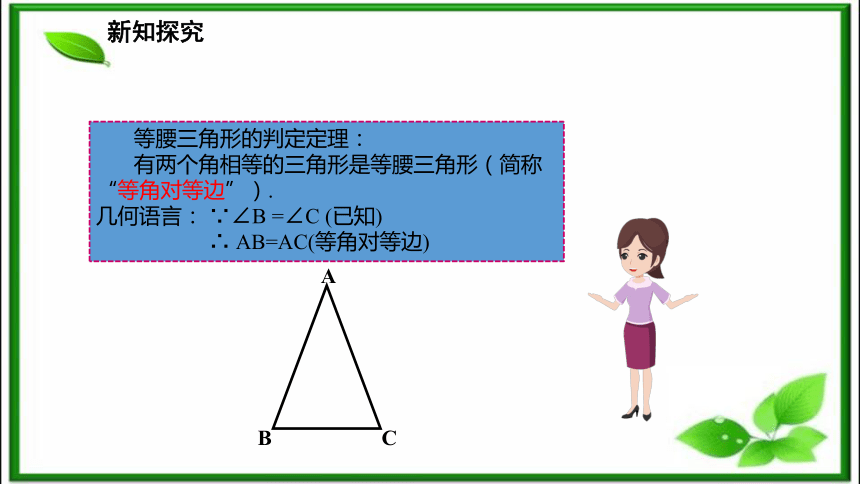
∠ADB=∠ADC.新知探究沿AD所在直线折叠,由于∠ADB=∠ADC,∠1=∠2,所以射线DB与射线DC重合,射线AB与射线AC重合.从而点B与点C重合,于是AB=AC.新知探究 等腰三角形的判定定理:
有两个角相等的三角形是等腰三角形(简称“等角对等边”).
几何语言: ∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
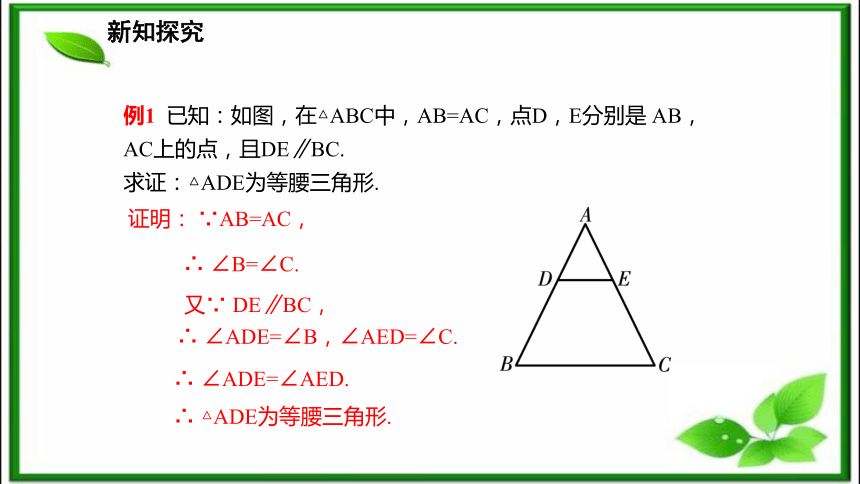
新知探究例1 已知:如图,在△ABC中,AB=AC,点D,E分别是 AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.证明: ∵AB=AC,∴ ∠B=∠C.又∵ DE∥BC,∴ ∠ADE=∠B,∠AED=∠C.∴ ∠ADE=∠AED.∴ △ADE为等腰三角形.新知探究例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.总结:角平分线+平行线=等腰三角形例3 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE
是∠BAC的平分线,AE与CD交于点F.
求证:△CEF是等腰三角形.证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.新知探究新知探究 由等腰三角形的判定定理可以直接得到:
定理1:三个角都相等的三角形是等边三角形.
定理2:有一个角是60°的等腰三角形是等边三角形.
新知探究证明定理2: 有一个角是60°的等腰三角形是等边三角形.证明:如图,在等腰三角形ABC中,AB=AC由三角形内角和定理得∠A+∠B+∠C= 180°.如果顶角∠A=60°,则∠B+∠C= 180°-60°=120°.又 AB=AC,∴ ∠B=∠C.∴ ∠B=∠C=∠A=60°.∴ △ABC是等边三角形.如果底角∠B=60°(或∠C=60°)同样可以证明△ABC是等边三角形.新知探究根据条件判断下列三角形是否为等边三角形.(1)(2)(6)(5)不
是是是是是(4)(3)不一定
是新知探究例4 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.证明:∵ △ABC是等边三角形,∴ ∠A= ∠B= ∠C.∵ DE∥BC,∴ ∠ADE= ∠B, ∠ AED= ∠C.∴ ∠A= ∠ADE= ∠ AED.∴ △ADE是等边三角形.新知探究变式1 若点D,E 在边AB,AC 的反向延长线上,
且DE∥BC,结论依然成立吗? 证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.新知探究变式2:上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.解:是等边三角形.理由如下:∵ △ABC是等边三角形,∴ ∠A= 60°.∵ AD=AE,∴ △ADE是等腰三角形.
∴ △ADE是等边三角形.课堂小结等腰(边)三角形的判定1.三个角都相等的三角形是等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.等角对等边,注意是指同一个三角形中.课堂小测1.如图,已知∠A=36°,∠ABD=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.36°72°△ABC,△DBA,△BCD课堂小测2.如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.123.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为_____.9第2题图第3题图课堂小测4.已知:如图,四边形ABCD中,AB=AD,∠B=∠D.
求证:BC=CD.证明:连接BD.
∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠ABC-∠ABD=∠ADC-∠ADB,
即∠DBC=∠BDC,
∴BC=CD.证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE (等角对等边).课堂小测5.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
2.掌握等腰三角形和等边三角形的判定定理的运用.(难点)新课导入1、等腰三角形是怎样定义的?有两条边相等的三角形叫作等腰三角形.③等腰三角形是轴对称图形.② 等腰三角形顶角的平分线、底边上的中线、底边上的高重合 (简称“三线合一”).① 等腰三角形的两个底角相等.(简写成“等边对等角”)2、等腰三角形有哪些性质?复习新课导入把“等腰三角形的两个底角相等”改写成“如果------那么-----”的形式.如果一个三角形有两个角相等,那么这个三角形是等腰三角形.如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.新知探究已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?画一个△ABC,其中∠B=∠C=30°,请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?AB=AC你能验证你的结论吗?新知探究 如图,在△ABC中,∠B=∠C.沿过点A的直线把∠BAC对折,得∠BAC的平分线AD交BC于点D,得∠1=∠2.又∠B=∠C,由三角形内角和的性质得
∠ADB=∠ADC.新知探究沿AD所在直线折叠,由于∠ADB=∠ADC,∠1=∠2,所以射线DB与射线DC重合,射线AB与射线AC重合.从而点B与点C重合,于是AB=AC.新知探究 等腰三角形的判定定理:
有两个角相等的三角形是等腰三角形(简称“等角对等边”).
几何语言: ∵∠B =∠C (已知)
∴ AB=AC(等角对等边)
新知探究例1 已知:如图,在△ABC中,AB=AC,点D,E分别是 AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.证明: ∵AB=AC,∴ ∠B=∠C.又∵ DE∥BC,∴ ∠ADE=∠B,∠AED=∠C.∴ ∠ADE=∠AED.∴ △ADE为等腰三角形.新知探究例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.总结:角平分线+平行线=等腰三角形例3 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE
是∠BAC的平分线,AE与CD交于点F.
求证:△CEF是等腰三角形.证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.新知探究新知探究 由等腰三角形的判定定理可以直接得到:
定理1:三个角都相等的三角形是等边三角形.
定理2:有一个角是60°的等腰三角形是等边三角形.
新知探究证明定理2: 有一个角是60°的等腰三角形是等边三角形.证明:如图,在等腰三角形ABC中,AB=AC由三角形内角和定理得∠A+∠B+∠C= 180°.如果顶角∠A=60°,则∠B+∠C= 180°-60°=120°.又 AB=AC,∴ ∠B=∠C.∴ ∠B=∠C=∠A=60°.∴ △ABC是等边三角形.如果底角∠B=60°(或∠C=60°)同样可以证明△ABC是等边三角形.新知探究根据条件判断下列三角形是否为等边三角形.(1)(2)(6)(5)不
是是是是是(4)(3)不一定
是新知探究例4 如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.证明:∵ △ABC是等边三角形,∴ ∠A= ∠B= ∠C.∵ DE∥BC,∴ ∠ADE= ∠B, ∠ AED= ∠C.∴ ∠A= ∠ADE= ∠ AED.∴ △ADE是等边三角形.新知探究变式1 若点D,E 在边AB,AC 的反向延长线上,
且DE∥BC,结论依然成立吗? 证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.新知探究变式2:上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.解:是等边三角形.理由如下:∵ △ABC是等边三角形,∴ ∠A= 60°.∵ AD=AE,∴ △ADE是等腰三角形.
∴ △ADE是等边三角形.课堂小结等腰(边)三角形的判定1.三个角都相等的三角形是等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.等角对等边,注意是指同一个三角形中.课堂小测1.如图,已知∠A=36°,∠ABD=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.36°72°△ABC,△DBA,△BCD课堂小测2.如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.123.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为_____.9第2题图第3题图课堂小测4.已知:如图,四边形ABCD中,AB=AD,∠B=∠D.
求证:BC=CD.证明:连接BD.
∵AB=AD,
∴∠ABD=∠ADB.
∵∠ABC=∠ADC,
∴∠ABC-∠ABD=∠ADC-∠ADB,
即∠DBC=∠BDC,
∴BC=CD.证明:∵△ABC是等边三角形,BD是角平分线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE (等角对等边).课堂小测5.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.求证:BD=DE.
同课章节目录
