2.6 用尺规作三角形 课件(29张ppt)
文档属性
| 名称 | 2.6 用尺规作三角形 课件(29张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 325.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-05 00:00:00 | ||
图片预览






文档简介
课件29张PPT。第2章
三角形八年级数学湘教版·上册2.6.1已知三边作三角形授课人:XXXX教学目标1.画图,写出作图的主要画法;(重点)
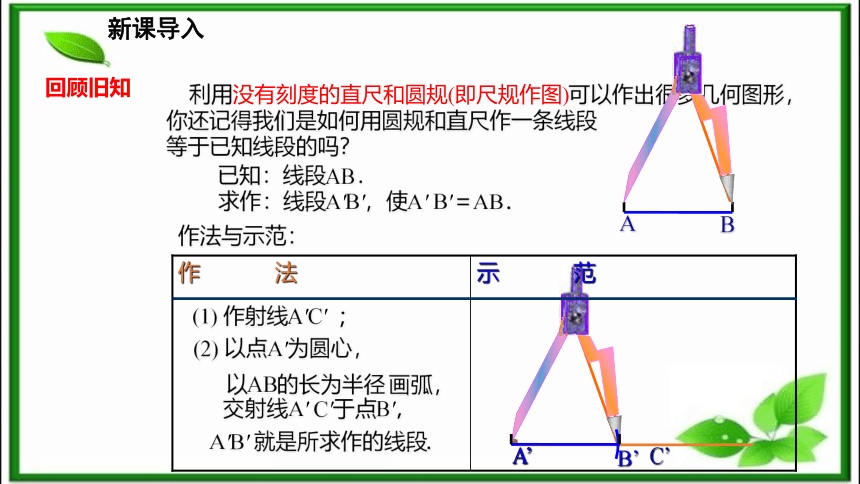
2.写出作图的主要画法,应用尺规作图.(难点)新课导入回顾旧知 利用没有刻度的直尺和圆规(即尺规作图)可以作出很多几何图形,你还记得我们是如何用圆规和直尺作一条线段
等于已知线段的吗?作法与示范:(1) 作射线A′C′ ;A’ C’(2) 以点A′为圆心,以AB的长为半径画弧, 交射线A′ C′于点B′, B’A′B′ 就是所求作的线段.新课导入基本作图:①作一条线段等于已知线段
②作一个角等于已知角
③作角的平分线
④作线段的垂直平分线
⑤过点作直线的垂线
⑥作三角形
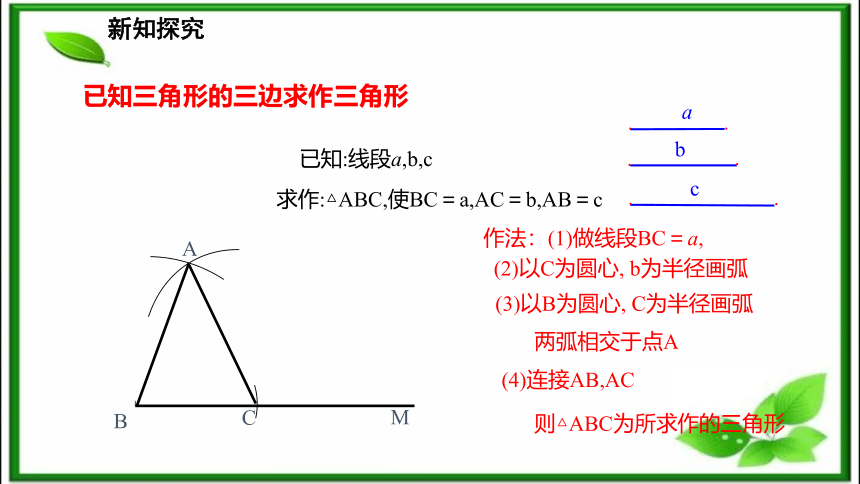
⑦作圆新知探究 根据三角形全等的判定条件,已知三边、两边及其夹角、两角及其夹边,都可以确定唯一的一个三角形.思考:怎么根据这些定理用尺规来作三角形呢?新知探究已知三角形的三边求作三角形已知:线段a,b,c求作:△ABC,使BC=a,AC=b,AB=c作法:(1)做线段BC=a, AC(2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形新知探究如图,已知线段a,h.
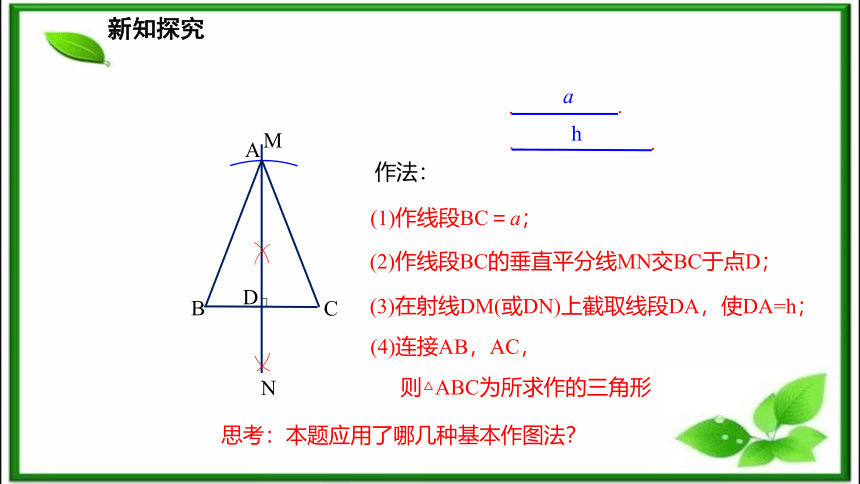
求作△ABC,使AB=AC,且BC=a,高AD=h.思考:①所作的图形是什么?满足哪些条件?②根据条件,你认为先作出等腰三角形的哪部分?③如何作底边上的高?底边上的高在什么线上?底边BC=a底边的垂直平分线已知底边及底边上的高作等腰三角形新知探究(1)作线段BC=a; (2)作线段BC的垂直平分线MN交BC于点D;(3)在射线DM(或DN)上截取线段DA,使DA=h;(4)连接AB,AC, 则△ABC为所求作的三角形作法:ADC BNM思考:本题应用了哪几种基本作图法?新知探究已知∠AOB,求作∠AOB的平分线.(1)在OA,OB上分别截取OD,OE,
使OD=OE;(2)分别以D,E为圆心,以大于 DE的长为半径画弧,在∠AOB内两弧交于点C;(3)作射线OC,DEC作法: 则OC为所求作的∠AOB的平分线.课堂小结根据条件作三角形已知底边及底边上的高作等腰三角形.已知三边作三角形.作角平分线.课堂小测1. 如图,一个机器零件上的两个孔的中心A,B已定好,又知第三个孔的中心C距A点1.5m,距B点1.8m. 如何找出C点的位置呢?答:以点A为圆心,1.5cm为半径画弧,再以点B为圆心,1.8cm为半径画弧,两弧的交点即为第三个孔的中心C.课堂小测2.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画 个. ABCDE4课堂小测3.如图,已知∠AOB.求作:∠AOB的补角的平分线(保留作图痕迹,不写作法).OABDC解:如图,∠AOB的补角为∠AOC,其平分线为射线OD.第2章 三角形八年级数学湘教版·上册2.6.2已知角和边作三角形授课人:XXXX教学目标1.画图,写出作图的主要画法;(重点)
2.出作图的主要画法,应用尺规作图.(难点) 直尺、量角器、圆规都是都是大家很熟悉的工具,大家都知道用直尺可以画线,用量角器可以画角,用圆规可以画圆.
如果只用无刻度的直尺和圆规,你还能画出符合条件的角吗? 新课导入新课导入回顾旧知如何作一个角等于已知角?
如图,已知∠AOB,求作一个角,使它等于∠AOB.D'C'B'O'A'(1)作射线O'A'; (2)以O为圆心, 任意长为半径画
弧,交OA于点C,交OB于点D;(3)以O'为圆心, OC(或OD)的长为半径画弧,交O'A'于点C';(4)以C'为圆心, CD长为半径画弧,交前弧于点D'; 则∠A'O'B'为所求作的角.作法:(5)过D'作射线O'B', BOA新课导入 运用所学知识,请说一说:为什么∠A'O'B'
就是所求作的角?解:由作图过程可知:△D'O'C'≌△DOC(SSS),所以∠D'O'C'=∠DOC,
即∠A'O'B'=∠AOB.O'C'=OC,O'D'=OD,D'C'=DC,新知探究已知两边及其夹角作三角形画一画:如图,已知∠α和线段 a, c. 求作△ABC,
使∠B=∠α,BC=a,BA=c.(2)在射线BM,BN上分别截取
BC=a,BA=c;(3)连接AC,则△ABC为所求作的三角形.作法:(1)作∠MBN= ∠α ; BNMCA 知识归纳(1)作∠···=∠ ··· ;(3)以···为顶点,以···为一边,作∠ ··· =∠ ··· ;(4)作一条线段··· = ··· ;(5)连接·· ,或连接··交··于点· · ;(6)分别以·· , ··为圆心,以·· , ···画弧,两弧交于···点;(2)在···上截取,使··· = ··· ;常用作图语言新知探究例1 如图所示,已知线段a,b,∠α,求作△ABC,使BC=a,AC=b,∠C= ∠α (不写作法,保留作图痕迹).分析:首先要完成 ∠α的作图问题,然后作出三角形.解:如图所示,△ABC即为所求.αabEDBAC新知探究已知两角及其夹边作三角形画一画:如图,已知∠α,∠β和线段a .
求作△ABC,使∠ABC=∠α,∠ACB=∠β,BC = a.A作法:(1)作线段BC = a;EDCB则△ABC为所求作的三角形.(2)在BC的同旁,作∠DBC=∠α,∠ECB=∠β,BD与CE相交于点A,已知线段a,b和∠α,求作△ABC,使其有一个内角等于∠α,且∠α的对边等于a,另有一边等于b.abα分析:先在草纸上画出一个假设的“已作出的三角形”;然后在草图上标出已给的边、角的对应位置;再找出边与角,确定作图的顺序.αbaaABMNCC'作法:
1、作∠MAN=∠α2、在射线AM上截取AB=b3、以B为圆心,以a为半径画弧,交AN
于点C, C'4、连接BC,BC'△ABC和△ABC'就是所求作的三角形.同样是已知两边及一角,为什么会出现两个三角形呢? 知识归纳 已知三角形的两边及一角并不都能只确定一个三角形.当已知两边及夹角时可以确定一个三角形,因此可以用来判定两个三角形全等;而当已知两边及一边的对角时,会画出两个不同的三角形,因此不能用来作为判别两个三角形全等的条件. 课堂小结根据条件作三角形已知两边及夹角作三角形,SAS.作一个角等于已知角.已知两角及夹边作三角形,ASA.课堂小测用尺规完成下列作图(只保留作图痕迹,不要求写出作法).1. 用尺规作一个角等于90°.解:如图所示,
①在直线l上截取线段PA,PB,
使PA=PB;
②分别以点A,B为圆心,大于
PA的任意长度为半径画弧,
两弧相交于点C.
③连接CP,则∠CPA= ∠CPB= 90°.·PABCl课堂小测2. 如图,已知线段a,b,求作一个直角三角形,
使它的两直角边分别为a和b.作法:
①作∠MCN=90°.
②在射线CM上截取CA=a,
在射线CN上截取CB=b.
③连接AB,则△ABC就是所求作的三
角形.abab课堂小测3. 如图,已知线段a和锐角∠α,求作一个Rt△ABC,使∠ACB=90°,∠B=∠α,BC=a.作法:
①作∠MCN=90°.
②在射线CM上截取CB=a.
③以B为顶点,BC为一边,
在CM的上侧作∠CBA=∠α,
交CN于A,
则△ABC就是所求作的三角形.MNCBA·
2.写出作图的主要画法,应用尺规作图.(难点)新课导入回顾旧知 利用没有刻度的直尺和圆规(即尺规作图)可以作出很多几何图形,你还记得我们是如何用圆规和直尺作一条线段
等于已知线段的吗?作法与示范:(1) 作射线A′C′ ;A’ C’(2) 以点A′为圆心,以AB的长为半径画弧, 交射线A′ C′于点B′, B’A′B′ 就是所求作的线段.新课导入基本作图:①作一条线段等于已知线段
②作一个角等于已知角
③作角的平分线
④作线段的垂直平分线
⑤过点作直线的垂线
⑥作三角形
⑦作圆新知探究 根据三角形全等的判定条件,已知三边、两边及其夹角、两角及其夹边,都可以确定唯一的一个三角形.思考:怎么根据这些定理用尺规来作三角形呢?新知探究已知三角形的三边求作三角形已知:线段a,b,c求作:△ABC,使BC=a,AC=b,AB=c作法:(1)做线段BC=a, AC(2)以C为圆心, b为半径画弧 (3)以B为圆心, C为半径画弧两弧相交于点A(4)连接AB,AC则△ABC为所求作的三角形新知探究如图,已知线段a,h.
求作△ABC,使AB=AC,且BC=a,高AD=h.思考:①所作的图形是什么?满足哪些条件?②根据条件,你认为先作出等腰三角形的哪部分?③如何作底边上的高?底边上的高在什么线上?底边BC=a底边的垂直平分线已知底边及底边上的高作等腰三角形新知探究(1)作线段BC=a; (2)作线段BC的垂直平分线MN交BC于点D;(3)在射线DM(或DN)上截取线段DA,使DA=h;(4)连接AB,AC, 则△ABC为所求作的三角形作法:ADC BNM思考:本题应用了哪几种基本作图法?新知探究已知∠AOB,求作∠AOB的平分线.(1)在OA,OB上分别截取OD,OE,
使OD=OE;(2)分别以D,E为圆心,以大于 DE的长为半径画弧,在∠AOB内两弧交于点C;(3)作射线OC,DEC作法: 则OC为所求作的∠AOB的平分线.课堂小结根据条件作三角形已知底边及底边上的高作等腰三角形.已知三边作三角形.作角平分线.课堂小测1. 如图,一个机器零件上的两个孔的中心A,B已定好,又知第三个孔的中心C距A点1.5m,距B点1.8m. 如何找出C点的位置呢?答:以点A为圆心,1.5cm为半径画弧,再以点B为圆心,1.8cm为半径画弧,两弧的交点即为第三个孔的中心C.课堂小测2.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画 个. ABCDE4课堂小测3.如图,已知∠AOB.求作:∠AOB的补角的平分线(保留作图痕迹,不写作法).OABDC解:如图,∠AOB的补角为∠AOC,其平分线为射线OD.第2章 三角形八年级数学湘教版·上册2.6.2已知角和边作三角形授课人:XXXX教学目标1.画图,写出作图的主要画法;(重点)
2.出作图的主要画法,应用尺规作图.(难点) 直尺、量角器、圆规都是都是大家很熟悉的工具,大家都知道用直尺可以画线,用量角器可以画角,用圆规可以画圆.
如果只用无刻度的直尺和圆规,你还能画出符合条件的角吗? 新课导入新课导入回顾旧知如何作一个角等于已知角?
如图,已知∠AOB,求作一个角,使它等于∠AOB.D'C'B'O'A'(1)作射线O'A'; (2)以O为圆心, 任意长为半径画
弧,交OA于点C,交OB于点D;(3)以O'为圆心, OC(或OD)的长为半径画弧,交O'A'于点C';(4)以C'为圆心, CD长为半径画弧,交前弧于点D'; 则∠A'O'B'为所求作的角.作法:(5)过D'作射线O'B', BOA新课导入 运用所学知识,请说一说:为什么∠A'O'B'
就是所求作的角?解:由作图过程可知:△D'O'C'≌△DOC(SSS),所以∠D'O'C'=∠DOC,
即∠A'O'B'=∠AOB.O'C'=OC,O'D'=OD,D'C'=DC,新知探究已知两边及其夹角作三角形画一画:如图,已知∠α和线段 a, c. 求作△ABC,
使∠B=∠α,BC=a,BA=c.(2)在射线BM,BN上分别截取
BC=a,BA=c;(3)连接AC,则△ABC为所求作的三角形.作法:(1)作∠MBN= ∠α ; BNMCA 知识归纳(1)作∠···=∠ ··· ;(3)以···为顶点,以···为一边,作∠ ··· =∠ ··· ;(4)作一条线段··· = ··· ;(5)连接·· ,或连接··交··于点· · ;(6)分别以·· , ··为圆心,以·· , ···画弧,两弧交于···点;(2)在···上截取,使··· = ··· ;常用作图语言新知探究例1 如图所示,已知线段a,b,∠α,求作△ABC,使BC=a,AC=b,∠C= ∠α (不写作法,保留作图痕迹).分析:首先要完成 ∠α的作图问题,然后作出三角形.解:如图所示,△ABC即为所求.αabEDBAC新知探究已知两角及其夹边作三角形画一画:如图,已知∠α,∠β和线段a .
求作△ABC,使∠ABC=∠α,∠ACB=∠β,BC = a.A作法:(1)作线段BC = a;EDCB则△ABC为所求作的三角形.(2)在BC的同旁,作∠DBC=∠α,∠ECB=∠β,BD与CE相交于点A,已知线段a,b和∠α,求作△ABC,使其有一个内角等于∠α,且∠α的对边等于a,另有一边等于b.abα分析:先在草纸上画出一个假设的“已作出的三角形”;然后在草图上标出已给的边、角的对应位置;再找出边与角,确定作图的顺序.αbaaABMNCC'作法:
1、作∠MAN=∠α2、在射线AM上截取AB=b3、以B为圆心,以a为半径画弧,交AN
于点C, C'4、连接BC,BC'△ABC和△ABC'就是所求作的三角形.同样是已知两边及一角,为什么会出现两个三角形呢? 知识归纳 已知三角形的两边及一角并不都能只确定一个三角形.当已知两边及夹角时可以确定一个三角形,因此可以用来判定两个三角形全等;而当已知两边及一边的对角时,会画出两个不同的三角形,因此不能用来作为判别两个三角形全等的条件. 课堂小结根据条件作三角形已知两边及夹角作三角形,SAS.作一个角等于已知角.已知两角及夹边作三角形,ASA.课堂小测用尺规完成下列作图(只保留作图痕迹,不要求写出作法).1. 用尺规作一个角等于90°.解:如图所示,
①在直线l上截取线段PA,PB,
使PA=PB;
②分别以点A,B为圆心,大于
PA的任意长度为半径画弧,
两弧相交于点C.
③连接CP,则∠CPA= ∠CPB= 90°.·PABCl课堂小测2. 如图,已知线段a,b,求作一个直角三角形,
使它的两直角边分别为a和b.作法:
①作∠MCN=90°.
②在射线CM上截取CA=a,
在射线CN上截取CB=b.
③连接AB,则△ABC就是所求作的三
角形.abab课堂小测3. 如图,已知线段a和锐角∠α,求作一个Rt△ABC,使∠ACB=90°,∠B=∠α,BC=a.作法:
①作∠MCN=90°.
②在射线CM上截取CB=a.
③以B为顶点,BC为一边,
在CM的上侧作∠CBA=∠α,
交CN于A,
则△ABC就是所求作的三角形.MNCBA·
同课章节目录
