12.4 综合实践与一次函数模型的应用 课件(共20张PPT)
文档属性
| 名称 | 12.4 综合实践与一次函数模型的应用 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 567.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-06 00:00:00 | ||
图片预览







文档简介
课件20张PPT。第十二章 一次函数八年级数学沪科版·上册12.4综合实践--一次函数模型的应用新课引入 乌鸦喝水,是《伊索寓言》中一个有趣的寓言故事.故事梗概为:"一只口渴的乌鸦看到窄口瓶内有半瓶水,于是将小石子投入瓶中,使水面升高,从而喝到了水."这个故事告诉人们遇到困难要积极地想解决办法,认真思考才能让问题迎刃而解.数学问题也一样哦.新知探究
现实生活或具体情境中的很多问题或现象都可以抽象成数学问题,并通过建立合适的数学模型来表示数量关系和变化规律,再求出结果并讨论结果的意义. 下面有一个实际问题,你能否利用已学的知识给予解决?新知探究
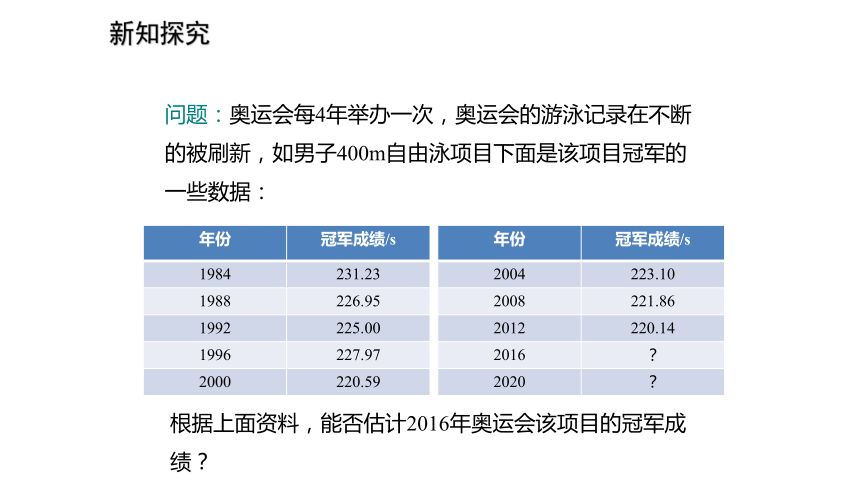
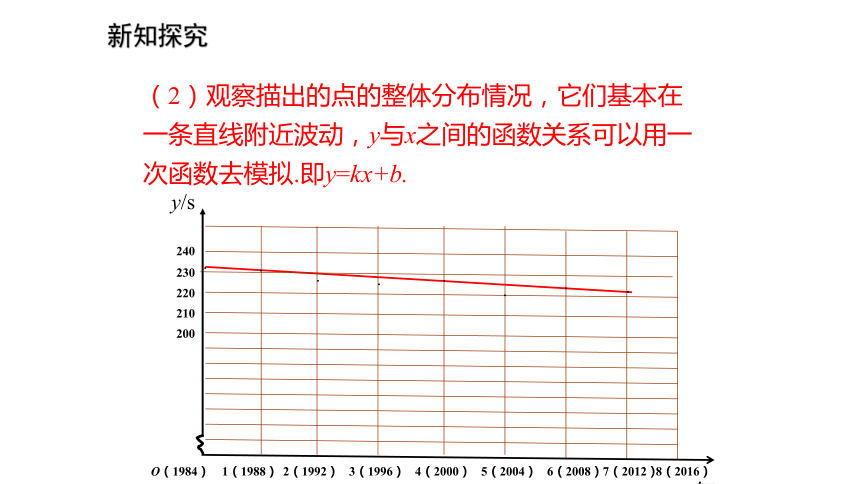
问题:奥运会每4年举办一次,奥运会的游泳记录在不断的被刷新,如男子400m自由泳项目下面是该项目冠军的一些数据:根据上面资料,能否估计2016年奥运会该项目的冠军成绩?新知探究 解:(1)以1984年为零点,每隔4年的年份的x值为横坐标,相应的y值为纵坐标,即(0,231.23),(1,226.95)等,在坐标系中描出这些对应点.O(1984)2301(1988)2(1992)3(1996)4(2000)5(2004)6(2008)7(2012)8(2016)y/sx/年210220200240新知探究(2)观察描出的点的整体分布情况,它们基本在一条直线附近波动,y与x之间的函数关系可以用一次函数去模拟.即y=kx+b.O(1984)2301(1988)2(1992)3(1996)4(2000)5(2004)6(2008)7(2012)8(2016)y/sx/年210220200240········新知探究 这里我们选取第1个点(0,231.23)及第7个点(7,221.86)的坐标代入y=kx+b中,得解得k=-1.34, b=231.23所以,一次函数的解析式为y=-1.34x+231.23.(3) 当把1984年的x值作为0,以后每增加4年得x的一个值,这样2016年时的x值为8,把x=8代入上式,得y=
-1.34×8+231.23=220.51(s)因此,可以得到2016年奥运会男子的自由泳的400m的冠军的成绩约是220.51s新知探究 2016年里约奥运会澳大利亚选手马克-霍顿以221.55s的成绩获得男子400m自由泳项目奥运会冠军,你对你预测的准确程度满意吗?新知探究 通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:(1)将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据
已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题.新知探究 例:小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
问题1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?新知探究3032383634424023252421222726y (码)x(厘米)问题2:据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?这些点在一条直线上,
如图所示.O新知探究 我们选取点(22,34)及
点(25,40)的坐标代入
y=kx+b中,得解得k=2, b=-10所以,一次函数的解析式为y=2x-10.把x=31代入上式,得y=2×31-10=52.因此,可以得到姚明穿52码的鞋子.课堂小结一次函数模型的应用①将得到的数据在直角坐标系中描出②观察这些点的特征,确定选用的函数模型,并根据已知数据求出具体的函数表达式③进行检验④应用这个函数模型解决问题课堂小测1.下图是用棋子摆成的“上”字 ,则第n个图共有多少枚棋子?
解:先列表:描点:如图所示.课堂小测 我们发现图形的变化规律为一条直线,我们可设该直线为
y=kx+b.
选取点(1,6)及
点(2,10)的坐标代入
y=kx+b中,
得解得k=4, b=2,所以,一次函数的解析式为y=4x+2.把x=n 代入上式,得y=4n+2.因此,可以得到第n个图形有(4n+2)枚棋子.课堂小测 2.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(?)计量法.两种计量法之间有如下对应关系:(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
(2)确定y与x之间的函数表达式,并加以检验;
(3)华氏0度时的温度应是多少摄氏度?
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?课堂小测(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;课堂小测(2)确定y与x之间的函数表达式,并加以检验;解:设y=kx+b,把(0,32)和(10,50)代入得解得经检验,点(20,68),(30,86),
(40,104),(50,122)的坐标均能满足上述表达式,
所以y与x之间的函数表达式为课堂小测(3)华氏0度时的温度应是多少摄氏度?解:当y=0时,解得∴华氏0度时的温度应是 摄氏度;课堂小测(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?解:把y=x代入,解得∴华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
现实生活或具体情境中的很多问题或现象都可以抽象成数学问题,并通过建立合适的数学模型来表示数量关系和变化规律,再求出结果并讨论结果的意义. 下面有一个实际问题,你能否利用已学的知识给予解决?新知探究
问题:奥运会每4年举办一次,奥运会的游泳记录在不断的被刷新,如男子400m自由泳项目下面是该项目冠军的一些数据:根据上面资料,能否估计2016年奥运会该项目的冠军成绩?新知探究 解:(1)以1984年为零点,每隔4年的年份的x值为横坐标,相应的y值为纵坐标,即(0,231.23),(1,226.95)等,在坐标系中描出这些对应点.O(1984)2301(1988)2(1992)3(1996)4(2000)5(2004)6(2008)7(2012)8(2016)y/sx/年210220200240新知探究(2)观察描出的点的整体分布情况,它们基本在一条直线附近波动,y与x之间的函数关系可以用一次函数去模拟.即y=kx+b.O(1984)2301(1988)2(1992)3(1996)4(2000)5(2004)6(2008)7(2012)8(2016)y/sx/年210220200240········新知探究 这里我们选取第1个点(0,231.23)及第7个点(7,221.86)的坐标代入y=kx+b中,得解得k=-1.34, b=231.23所以,一次函数的解析式为y=-1.34x+231.23.(3) 当把1984年的x值作为0,以后每增加4年得x的一个值,这样2016年时的x值为8,把x=8代入上式,得y=
-1.34×8+231.23=220.51(s)因此,可以得到2016年奥运会男子的自由泳的400m的冠军的成绩约是220.51s新知探究 2016年里约奥运会澳大利亚选手马克-霍顿以221.55s的成绩获得男子400m自由泳项目奥运会冠军,你对你预测的准确程度满意吗?新知探究 通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:(1)将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据
已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题.新知探究 例:小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
问题1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?新知探究3032383634424023252421222726y (码)x(厘米)问题2:据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?这些点在一条直线上,
如图所示.O新知探究 我们选取点(22,34)及
点(25,40)的坐标代入
y=kx+b中,得解得k=2, b=-10所以,一次函数的解析式为y=2x-10.把x=31代入上式,得y=2×31-10=52.因此,可以得到姚明穿52码的鞋子.课堂小结一次函数模型的应用①将得到的数据在直角坐标系中描出②观察这些点的特征,确定选用的函数模型,并根据已知数据求出具体的函数表达式③进行检验④应用这个函数模型解决问题课堂小测1.下图是用棋子摆成的“上”字 ,则第n个图共有多少枚棋子?
解:先列表:描点:如图所示.课堂小测 我们发现图形的变化规律为一条直线,我们可设该直线为
y=kx+b.
选取点(1,6)及
点(2,10)的坐标代入
y=kx+b中,
得解得k=4, b=2,所以,一次函数的解析式为y=4x+2.把x=n 代入上式,得y=4n+2.因此,可以得到第n个图形有(4n+2)枚棋子.课堂小测 2.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(?)计量法.两种计量法之间有如下对应关系:(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
(2)确定y与x之间的函数表达式,并加以检验;
(3)华氏0度时的温度应是多少摄氏度?
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?课堂小测(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;课堂小测(2)确定y与x之间的函数表达式,并加以检验;解:设y=kx+b,把(0,32)和(10,50)代入得解得经检验,点(20,68),(30,86),
(40,104),(50,122)的坐标均能满足上述表达式,
所以y与x之间的函数表达式为课堂小测(3)华氏0度时的温度应是多少摄氏度?解:当y=0时,解得∴华氏0度时的温度应是 摄氏度;课堂小测(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?解:把y=x代入,解得∴华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
