15.2 线段的垂直平分线 课件(共25张PPT)
文档属性
| 名称 | 15.2 线段的垂直平分线 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-06 00:00:00 | ||
图片预览



文档简介
课件25张PPT。第十五章 轴对称图形与
等腰三角形八年级数学沪科版·上册15.2线段的垂直平分线新课引入 市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处才能使得它到三个小区的距离相等?ABC新知探究
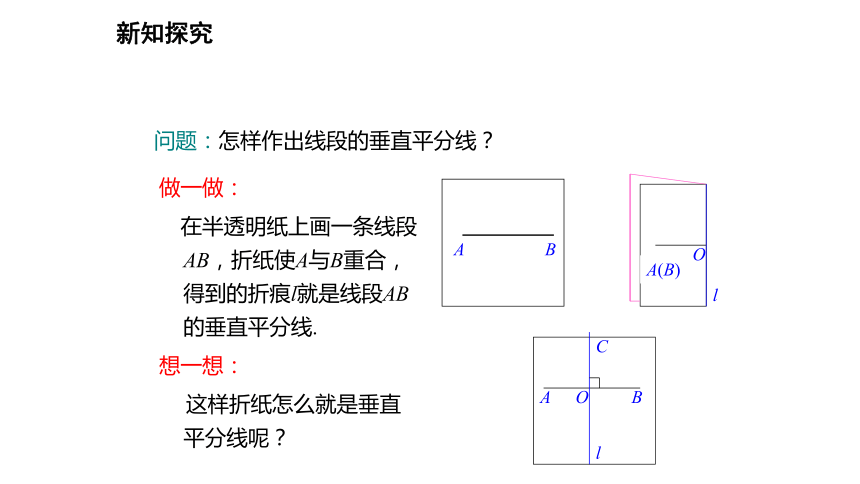
问题:怎样作出线段的垂直平分线?做一做:
在半透明纸上画一条线段AB,折纸使A与B重合,得到的折痕l就是线段AB的垂直平分线.
想一想:
这样折纸怎么就是垂直平分线呢?ABA(B)ABlOlCO新知探究
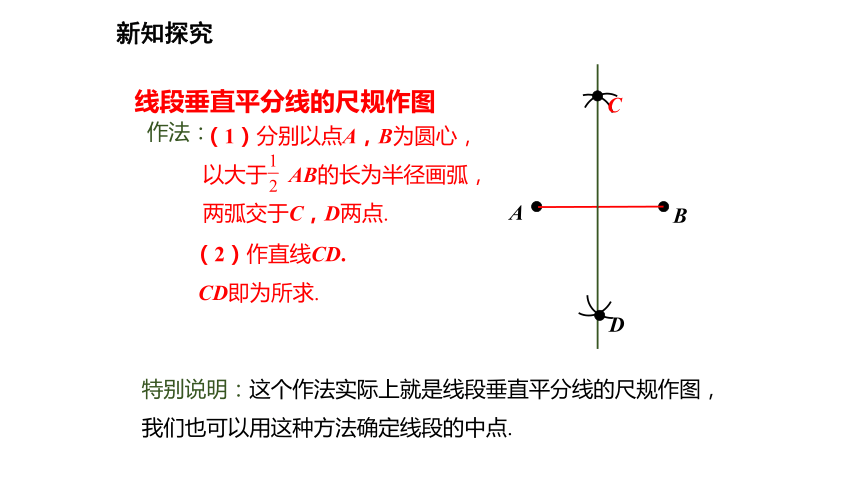
作法:(2)作直线CD.
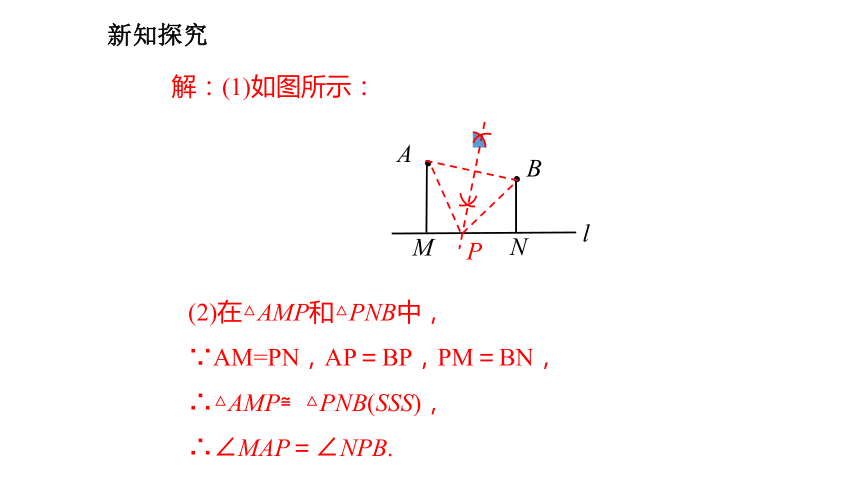
CD即为所求.特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.线段垂直平分线的尺规作图例1 如图,已知点A、点B以及直线l.
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
(2)在(1)所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.新知探究
新知探究解:(1)如图所示:(2)在△AMP和△PNB中,
∵AM=PN,AP=BP,PM=BN,
∴△AMP≌△PNB(SSS),
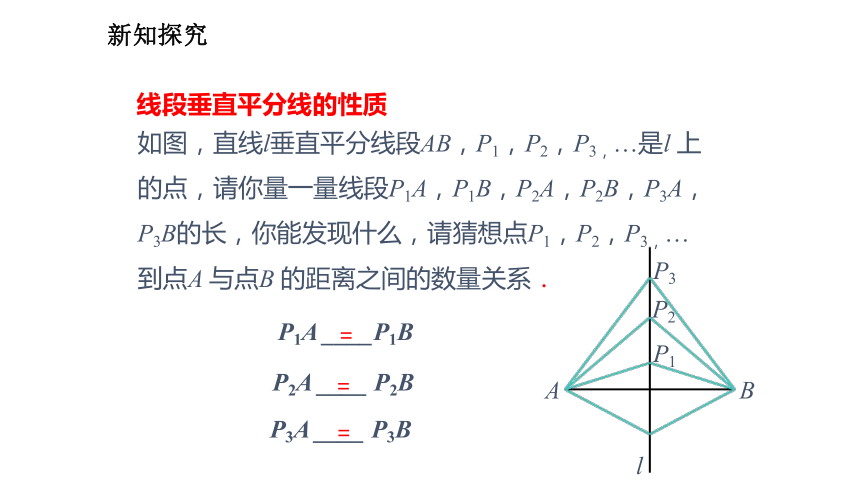
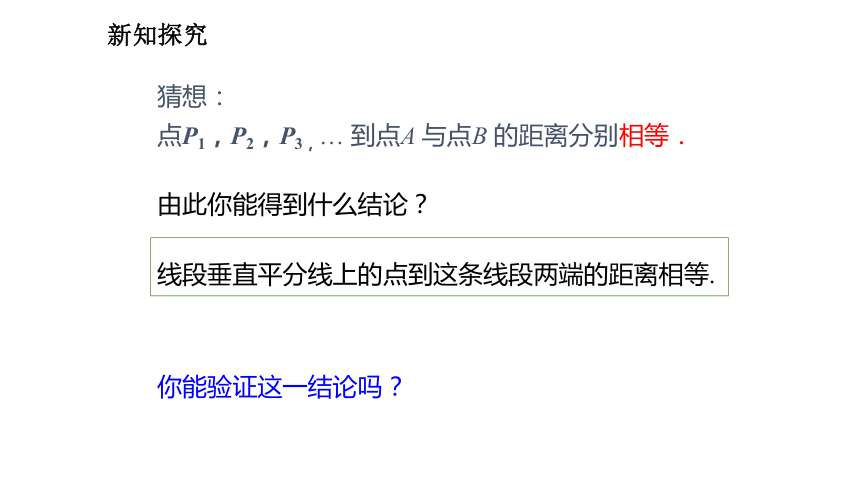
∴∠MAP=∠NPB.P新知探究线段垂直平分线的性质如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么,请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.P1A ____P1BP2A ____ P2BP3A ____ P3B===新知探究猜想:
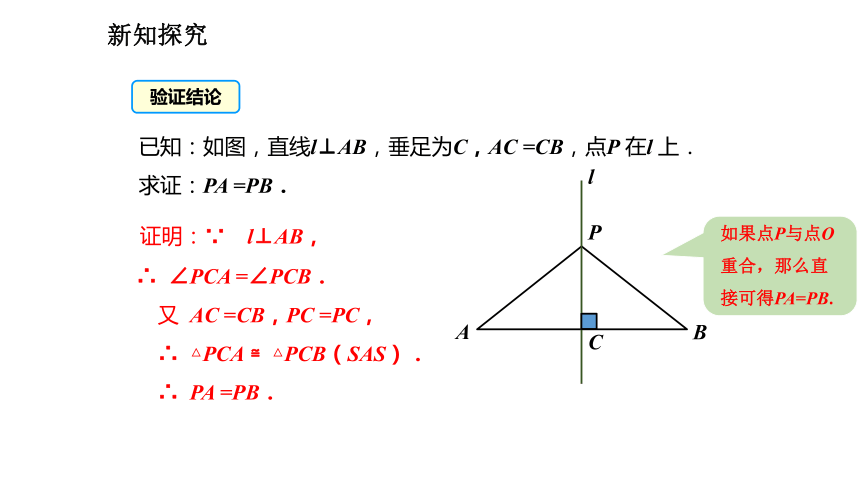
点P1,P2,P3,… 到点A 与点B 的距离分别相等. 线段垂直平分线上的点到这条线段两端的距离相等.由此你能得到什么结论?你能验证这一结论吗?新知探究 已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB. 证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.验证结论如果点P与点O重合,那么直接可得PA=PB.新知探究例2 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,求BC的长.解:∵△DBC的周长为BC+BD+CD=35cm,
又∵DE垂直平分AB,∴AD=BD,
故BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).【方法总结】利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.新知探究练一练:1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 32.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .B10cm图①新知探究例3 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.新知探究证明:(1)∵AD∥BC,
∴∠ADC=∠ECF.
∵E是CD的中点,∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,
∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF.
∵AD=CF, ∴AB=BC+AD.新知探究定理:线段垂直平分线上的点到线段两端的距离相等.逆
命
题到线段两端距离相等的点在线段的垂直平分线上.它是真命题吗?你能证明吗? 线段垂直平分线的判定新知探究已知:PA=PB,
求证:点P在线段AB的垂直平分线上.证明:作PC⊥AB,垂足为C.∴∠ACP=∠BCP=90°.在Rt△ACP和Rt△BCP中,∴Rt△ACP≌Rt△BCP(HL),∴AC=BC,∴点P在线段AB的垂直平分线上.PA=PB,
PC=PC,新知探究线段垂直平分线的判定与线段两个端点距离相等的点在这条线段的垂直平分线上.应用格式:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.作用:判断一个点是否在线段的垂直平分线上.新知探究例4 如图,已知△ABC的边AB,AC的垂直平分线相交于点P. 求证:点P在BC的垂直平分线上.
BCAP证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上,
∴PA=PB,PA=PC,
(线段垂直平分线上的点到线段两端的距离相等)
∴PB=PC,(等量代换)
∴点P在BC的垂直平分线上.
(到线段两端距离相等的点在这条线段的垂直平分线上)新知探究总结归纳 三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.现在你能回答讲课前提出的问题吗?
你知道购物中心应该建在何处了吗?新知探究例5 已知:如图,点E是∠AOB平分线上的一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.证明:∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴DE=CE(角平分线上的点到角的两边的距离相等).∴ OE是CD的垂直平分线.课堂小结线段的垂直平分的性质和判定性质到线段的两端距离相等的点在线段的垂直平分线上 内容判定内容作用线段的垂直平分线上的点到线段的两端的距离相等 作用见垂直平分线,得线段相等判断一个点是否在线段的垂直平分线上D课堂小测2.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .A3.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点D课堂小测4.如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上.
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________.(-3,0)(-m,0)OCBAyx课堂小测5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.16课堂小测6.如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.BC学校在连接任意两点的两条线段的垂直平分线的交点处.A课堂小测
问题:怎样作出线段的垂直平分线?做一做:
在半透明纸上画一条线段AB,折纸使A与B重合,得到的折痕l就是线段AB的垂直平分线.
想一想:
这样折纸怎么就是垂直平分线呢?ABA(B)ABlOlCO新知探究
作法:(2)作直线CD.
CD即为所求.特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.线段垂直平分线的尺规作图例1 如图,已知点A、点B以及直线l.
(1)用尺规作图的方法在直线l上求作一点P,使PA=PB.(保留作图痕迹,不要求写出作法);
(2)在(1)所作的图中,若AM=PN,BN=PM,求证:∠MAP=∠NPB.新知探究
新知探究解:(1)如图所示:(2)在△AMP和△PNB中,
∵AM=PN,AP=BP,PM=BN,
∴△AMP≌△PNB(SSS),
∴∠MAP=∠NPB.P新知探究线段垂直平分线的性质如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么,请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.P1A ____P1BP2A ____ P2BP3A ____ P3B===新知探究猜想:
点P1,P2,P3,… 到点A 与点B 的距离分别相等. 线段垂直平分线上的点到这条线段两端的距离相等.由此你能得到什么结论?你能验证这一结论吗?新知探究 已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB. 证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.验证结论如果点P与点O重合,那么直接可得PA=PB.新知探究例2 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,求BC的长.解:∵△DBC的周长为BC+BD+CD=35cm,
又∵DE垂直平分AB,∴AD=BD,
故BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).【方法总结】利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.新知探究练一练:1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 32.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .B10cm图①新知探究例3 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)根据线段垂直平分线的性质判断出AB=BF即可.新知探究证明:(1)∵AD∥BC,
∴∠ADC=∠ECF.
∵E是CD的中点,∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,
∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF.
∵AD=CF, ∴AB=BC+AD.新知探究定理:线段垂直平分线上的点到线段两端的距离相等.逆
命
题到线段两端距离相等的点在线段的垂直平分线上.它是真命题吗?你能证明吗? 线段垂直平分线的判定新知探究已知:PA=PB,
求证:点P在线段AB的垂直平分线上.证明:作PC⊥AB,垂足为C.∴∠ACP=∠BCP=90°.在Rt△ACP和Rt△BCP中,∴Rt△ACP≌Rt△BCP(HL),∴AC=BC,∴点P在线段AB的垂直平分线上.PA=PB,
PC=PC,新知探究线段垂直平分线的判定与线段两个端点距离相等的点在这条线段的垂直平分线上.应用格式:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.作用:判断一个点是否在线段的垂直平分线上.新知探究例4 如图,已知△ABC的边AB,AC的垂直平分线相交于点P. 求证:点P在BC的垂直平分线上.
BCAP证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上,
∴PA=PB,PA=PC,
(线段垂直平分线上的点到线段两端的距离相等)
∴PB=PC,(等量代换)
∴点P在BC的垂直平分线上.
(到线段两端距离相等的点在这条线段的垂直平分线上)新知探究总结归纳 三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.现在你能回答讲课前提出的问题吗?
你知道购物中心应该建在何处了吗?新知探究例5 已知:如图,点E是∠AOB平分线上的一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.证明:∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴DE=CE(角平分线上的点到角的两边的距离相等).∴ OE是CD的垂直平分线.课堂小结线段的垂直平分的性质和判定性质到线段的两端距离相等的点在线段的垂直平分线上 内容判定内容作用线段的垂直平分线上的点到线段的两端的距离相等 作用见垂直平分线,得线段相等判断一个点是否在线段的垂直平分线上D课堂小测2.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .A3.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点D课堂小测4.如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上.
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________.(-3,0)(-m,0)OCBAyx课堂小测5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.16课堂小测6.如图,有A,B,C三个村庄,现准备要建一所希望小学,要求学校到三个村庄的距离相等,请你确定学校的位置.BC学校在连接任意两点的两条线段的垂直平分线的交点处.A课堂小测
