湘教版八年级上册4.2.1不等式的基本性质1 课件(17张ppt)
文档属性
| 名称 | 湘教版八年级上册4.2.1不等式的基本性质1 课件(17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-06 00:00:00 | ||
图片预览





文档简介
课件17张PPT。第四章
一元一次不等式(组)八年级数学湘教版·上册4.2.1不等式的基本性质1授课人:XXXX学习目标
1.理解并掌握不等式的基本性质1;
2.通过实例操作,培养学生观察、分析、比较的能力,会用不等式的基本性质1进行不等式的变形.
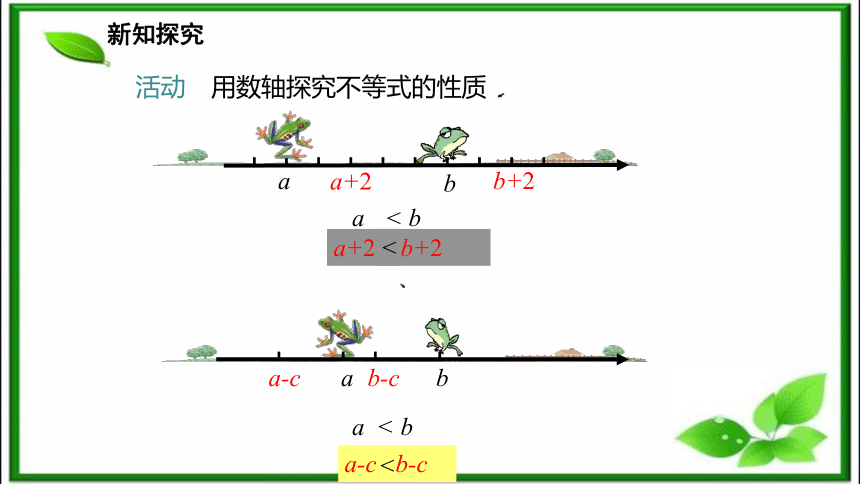
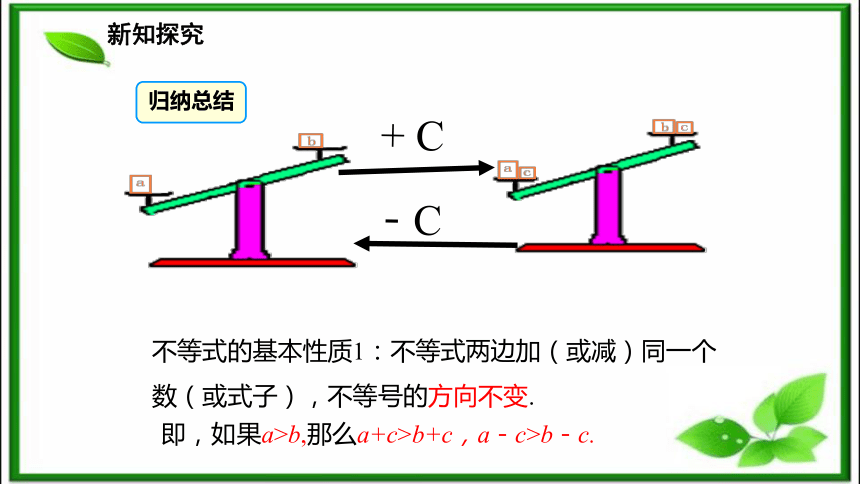
(重点、难点)新课导入我比你大两岁,所以我是你哥哥大两岁,那三年前,你不就比我小呀哈哈!三年前我还是比你大哦?那....再过十年,我肯定比你大.呵呵,再过二十年,你也比我小!新知探究 1.用不等号填空:(1)5 3 ; 5+2 3+2 ;5-2 3-2 .> > > < < < 新知探究2. 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果. 100 -a 84 -a>请用“>”或“<”填空: 100 –a+b 84 –a+b>思考:你发现什么规律了吗?新知探究abb+2a+2a ba+2 b+2abb-ca-ca < ba-c b-c<<<活动 用数轴探究不等式的性质新知探究+ C-C不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.即,如果a>b,那么a+c>b+c,a-c>b-c.归纳总结新知探究 解: 因为 a>b,两边都加上3, 因为 a b+3; 由不等式的基本性质1,得 a-5 < b-5 .(1)已知 a>b,则a+3 b+3(2)已知 a < 例1 用“>”或“<”填空:新知探究 用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据 ;
(2)若a-2<3,则a______5,
根据 .> < 不等式的基本性质1不等式的基本性质1新知探究(1) x + 6 > 5,解:不等式的两边都减去6,由不等式的基本性质1,得x +6-6 > 5-6,即 x > -1.(2) 3x < 2x -2,不等式的两边都减去2x,由不等式的基本性质1,得 3x -2x < 2x-2-2x,即 x < -2.例2 把下列不等式化为x >a或x< a的形式:(1)x + 6 > 5 ;(2) 3x < 2x -2 .为什么不等式两边都减去2x?新知探究 由(2)可以看出,运用不等式基本性质1 对 3x < 2x-2 进行化简的过程,就是对不等式3x< 2x-2 作了如下变形:3x < 2x -23x<2x-2- 把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.新知探究 下列变形中,正确的是( )
A. 由 3x -1< 2x - 2,得 x < -1
B. 由 2x +1>3x -1 ,得 x > -2
C. 由 2x + 1> x -1 ,得 x > 2
D. 由 x +2 < 2x - 2,得 x < 0A总结:移项只改变移动的项的符号,整个不等式的符号保持不变.新知探究议一议:我们知道三角形任意两边之和大于第三边,即如图所示,在△ABC中,有
AB + BC > AC,
BC + AC > AB,
AC + A B > BC .把上面的三个式子进行移项操作,你会得到什么?新知探究想一想:由不等式的变形,三角形的两边之差与第三边有何关系?三角形任意两边的差小于第三边新知探究例3 已知三角形△ABC,AB=3,AC=8,BC长为奇数,求BC的长.解:根据三角形的三边关系可得8-3<BC<8+3,
即5<BC<11.
∵BC为奇数,
∴BC的长为7或9.分析:根据三角形三边关系定理得到第三边的范围,再根据BC为奇数确定BC长即可.课堂小结不等式的基本性质1↓如果a>b,那么a+c>b+c,a-c>b-c(表达形式)↓三角形中,两边之差小于第三边课堂小测 1. 已知a < b,用“>”或“<”填空: (1)a +12 b +12 ; (2)b -10 a -10 .<>解:x < 2解:x < 62. 把下列不等式化为x>a或x
1.理解并掌握不等式的基本性质1;
2.通过实例操作,培养学生观察、分析、比较的能力,会用不等式的基本性质1进行不等式的变形.
(重点、难点)新课导入我比你大两岁,所以我是你哥哥大两岁,那三年前,你不就比我小呀哈哈!三年前我还是比你大哦?那....再过十年,我肯定比你大.呵呵,再过二十年,你也比我小!新知探究 1.用不等号填空:(1)5 3 ; 5+2 3+2 ;5-2 3-2 .> > > < < < 新知探究2. 水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果. 100 -a 84 -a>请用“>”或“<”填空: 100 –a+b 84 –a+b>思考:你发现什么规律了吗?新知探究abb+2a+2a ba+2 b+2abb-ca-ca < ba-c b-c<<<活动 用数轴探究不等式的性质新知探究+ C-C不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.即,如果a>b,那么a+c>b+c,a-c>b-c.归纳总结新知探究 解: 因为 a>b,两边都加上3, 因为 a
(1)若x+3>6,则x______3,
根据 ;
(2)若a-2<3,则a______5,
根据 .> < 不等式的基本性质1不等式的基本性质1新知探究(1) x + 6 > 5,解:不等式的两边都减去6,由不等式的基本性质1,得x +6-6 > 5-6,即 x > -1.(2) 3x < 2x -2,不等式的两边都减去2x,由不等式的基本性质1,得 3x -2x < 2x-2-2x,即 x < -2.例2 把下列不等式化为x >a或x< a的形式:(1)x + 6 > 5 ;(2) 3x < 2x -2 .为什么不等式两边都减去2x?新知探究 由(2)可以看出,运用不等式基本性质1 对 3x < 2x-2 进行化简的过程,就是对不等式3x< 2x-2 作了如下变形:3x < 2x -23x<2x-2- 把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.新知探究 下列变形中,正确的是( )
A. 由 3x -1< 2x - 2,得 x < -1
B. 由 2x +1>3x -1 ,得 x > -2
C. 由 2x + 1> x -1 ,得 x > 2
D. 由 x +2 < 2x - 2,得 x < 0A总结:移项只改变移动的项的符号,整个不等式的符号保持不变.新知探究议一议:我们知道三角形任意两边之和大于第三边,即如图所示,在△ABC中,有
AB + BC > AC,
BC + AC > AB,
AC + A B > BC .把上面的三个式子进行移项操作,你会得到什么?新知探究想一想:由不等式的变形,三角形的两边之差与第三边有何关系?三角形任意两边的差小于第三边新知探究例3 已知三角形△ABC,AB=3,AC=8,BC长为奇数,求BC的长.解:根据三角形的三边关系可得8-3<BC<8+3,
即5<BC<11.
∵BC为奇数,
∴BC的长为7或9.分析:根据三角形三边关系定理得到第三边的范围,再根据BC为奇数确定BC长即可.课堂小结不等式的基本性质1↓如果a>b,那么a+c>b+c,a-c>b-c(表达形式)↓三角形中,两边之差小于第三边课堂小测 1. 已知a < b,用“>”或“<”填空: (1)a +12 b +12 ; (2)b -10 a -10 .<>解:x < 2解:x < 62. 把下列不等式化为x>a或x
同课章节目录
