湘教版八年级上册5.1.2二次根式的化简 课件(17张ppt)
文档属性
| 名称 | 湘教版八年级上册5.1.2二次根式的化简 课件(17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 465.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-06 00:00:00 | ||
图片预览






文档简介
课件17张PPT。第五章
二次根式八年级数学湘教版·上册5.1.2二次根式的化简授课人:XXXX学习目标
1.能准确利用积的算术平方根的性质进行化简;(重点)
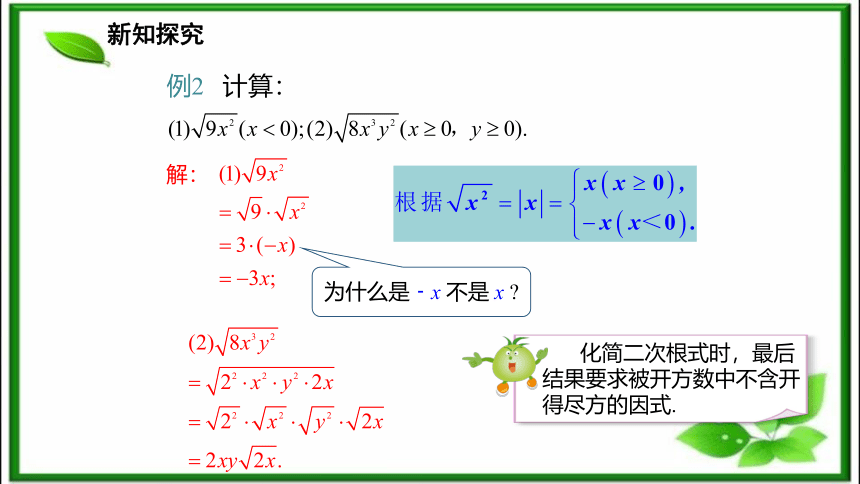
2.能准确将二次根式的计算结果用最简二次根式表 示出来.(难点)新课导入 1. 的性质: =a (a ≥0).2. 的性质: =a (a≥0).思考: 的值为多少?新知探究(1) = , = ;= , = ;662020填一填有何发现?= ,6.480= ;(2)用计算器计算:6.480一新知探究当a≥0,b≥0时,由于验证发现要点归纳(a≥0,b≥0). 积的算术平方根等于算术平方根的积新知探究例1 化简下列二次根式.解: 化简二次根式时,最后结果要求被开方数中不含开得尽方的因数.?新知探究例2 计算:解: 为什么是﹣x 不是 x ? 化简二次根式时,最后
结果要求被开方数中不含开
得尽方的因式.新知探究 在化简二次根式时,可以直接把根号下的每一个平方因子去掉平方号以后移到根号外
(注意:从根号下直接移到根号外的数必须是非负数).总结归纳新知探究例3 化简下列二次根式: 化简二次根式时,最后结果要求被开方数不含分母.解:注意: 表示的是 与 乘积,切勿理解为“和”.新知探究 从前面的例题可以看出,这些式子的最后结果,
具有以下特点:
(1) 被开方数中不含开得尽方的因数(或因式);
(2) 被开方数不含分母. 我们把满足上述两个条件的二次根式,叫作最简二次根式.新知探究 (m>0)是最简二次根式吗?如果不是,你能把它化简吗?解: 不是最简二次根式. 它含有能开方的因式 m2 . 新知探究例4. 化简:解:①② ③课堂小结积的算术平方根课堂小测 1.化简下列二次根式.解:课堂小测解: 2.化简下列二次根式.课堂小测 3.化简:解:注意: 最后化简的结果一般不写成 ,因为它属于单项式,其中 作为系数部分.课堂小测能力提升 4.化简: 解:
1.能准确利用积的算术平方根的性质进行化简;(重点)
2.能准确将二次根式的计算结果用最简二次根式表 示出来.(难点)新课导入 1. 的性质: =a (a ≥0).2. 的性质: =a (a≥0).思考: 的值为多少?新知探究(1) = , = ;= , = ;662020填一填有何发现?= ,6.480= ;(2)用计算器计算:6.480一新知探究当a≥0,b≥0时,由于验证发现要点归纳(a≥0,b≥0). 积的算术平方根等于算术平方根的积新知探究例1 化简下列二次根式.解: 化简二次根式时,最后结果要求被开方数中不含开得尽方的因数.?新知探究例2 计算:解: 为什么是﹣x 不是 x ? 化简二次根式时,最后
结果要求被开方数中不含开
得尽方的因式.新知探究 在化简二次根式时,可以直接把根号下的每一个平方因子去掉平方号以后移到根号外
(注意:从根号下直接移到根号外的数必须是非负数).总结归纳新知探究例3 化简下列二次根式: 化简二次根式时,最后结果要求被开方数不含分母.解:注意: 表示的是 与 乘积,切勿理解为“和”.新知探究 从前面的例题可以看出,这些式子的最后结果,
具有以下特点:
(1) 被开方数中不含开得尽方的因数(或因式);
(2) 被开方数不含分母. 我们把满足上述两个条件的二次根式,叫作最简二次根式.新知探究 (m>0)是最简二次根式吗?如果不是,你能把它化简吗?解: 不是最简二次根式. 它含有能开方的因式 m2 . 新知探究例4. 化简:解:①② ③课堂小结积的算术平方根课堂小测 1.化简下列二次根式.解:课堂小测解: 2.化简下列二次根式.课堂小测 3.化简:解:注意: 最后化简的结果一般不写成 ,因为它属于单项式,其中 作为系数部分.课堂小测能力提升 4.化简: 解:
同课章节目录
