湘教版5.2.2二次根式的除法 课件(27张ppt)
文档属性
| 名称 | 湘教版5.2.2二次根式的除法 课件(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 845.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览






文档简介
课件26张PPT。第五章
二次根式八年级数学湘教版·上册5.2.2二次根式的除法授课人:XXXX学习目标
1.理解二次根式的除法法则及商的算术平方根的性质.掌握最简二次根式的特点.(重点)
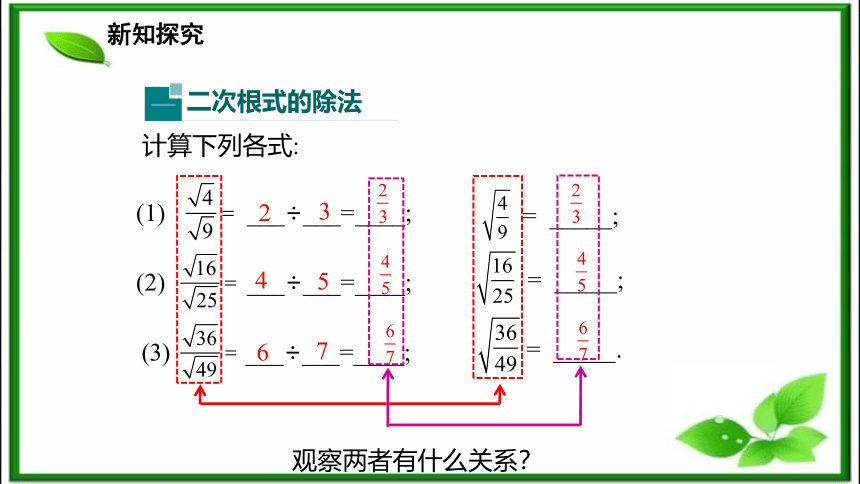
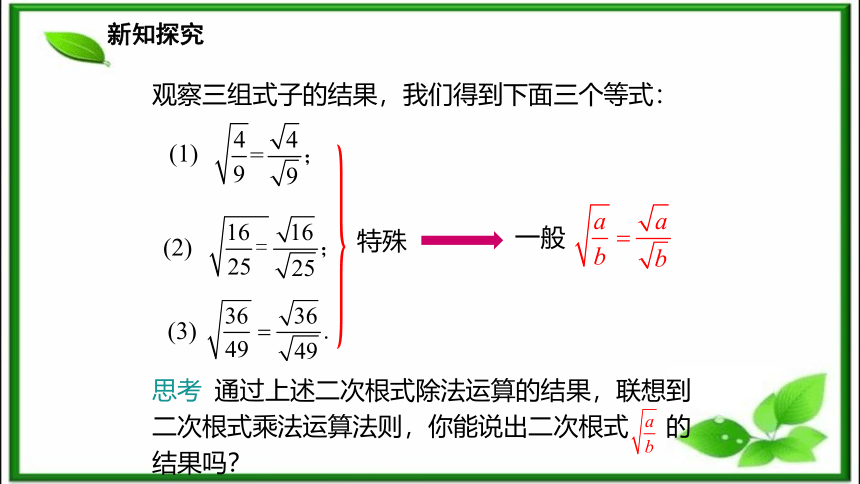
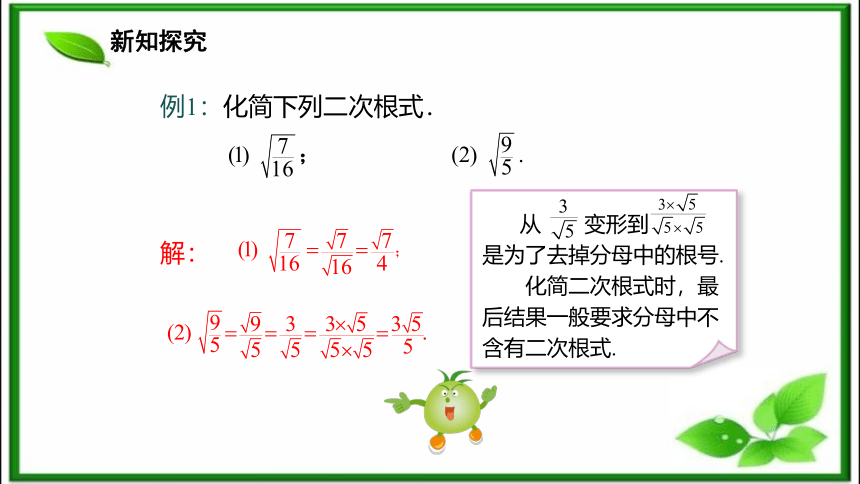
2.合理简洁地进行二次根式的除法运算.(难点)新课导入站在水平高度为h米的地方看见的水平距离为d米,它们近似地符合公式为 .解:问题1 某一登山者爬到海拔100米处,即 时,他看到的水平线的距离d1是多少?新知探究问题2 该登山者接着爬到海拔200米的山顶,即 时,此时他看到的水平线的距离d2是多少?问题3 他从海拔100米处登上海拔200米高的山顶,那么他看到的水平线的距离是原来的多少倍?解:二次根式的除法该怎样算呢?解:思考 乘法法则是如何得出的?除法有没有类似的法则?新知探究(1) ___÷___=____;= _____;计算下列各式:(2) ___÷___=____;(3) ___÷___=____;= _____;= _____.234567观察两者有什么关系? 新知探究观察三组式子的结果,我们得到下面三个等式:(1) (2) (3) 思考 通过上述二次根式除法运算的结果,联想到二次根式乘法运算法则,你能说出二次根式 的结果吗?特殊一般新知探究问题 在前面发现的规律 中,a,b的取值范围有没有限制呢?不对,同乘法法则一样,a,b都为非负数.a,b同号就可以啦!你们都错啦,a≥0,b>0,b=0时等式两边的二次根式就没有意义啦!新知探究归纳总结二次根式的商的算术平方根性质文字叙述:被开方数商的算术平方根等于算术平方根的商.当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得新知探究例1:化简下列二次根式.解: 从 变形到
是为了去掉分母中的根号.
化简二次根式时,最后结果一般要求分母中不含有二次根式.新知探究例2 化简:解:还有其他解法吗?补充解法:新知探究解:先应用商的算术平方根的性质,再运用积的平方根性质新知探究1.能使等式 成立的x的取值范围是( )
A.x≠2 B.x≥0 C.x>2 D.x≥2 C2.化简:解:新知探究我们可以运用它来进行二次根式的解题和化简.语言表述:积中各因式的算术平方根的商,等于商的算术平方根. 我们知道,把积的算术平方根的性质反过来就得到二次根式的乘法法则.类似的,把二次根式的商的算术平方根的性质反过来,就得到二次根式的除法法则:新知探究例3 计算: 新知探究例4 计算:解:除式是分数或分式时,先要转化为乘法再进行运算.新知探究解: 类似(4)中被开方数中含有带分数,应先将带分数化成假分数,再运用二次根式除法法则进行运算.
新知探究例5 设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.解:∵
∴新知探究例6 高空抛物现象被称为“悬在城市上空的痛”.据报道:一个30g的鸡蛋从18楼抛下来就可以砸破行人的头骨,从25楼抛下可以使人当场死亡.据研究从高空抛物时间t和高度h近似的满足公式 .从100米高空抛物到落地所需时间t2是从50米高空抛物到落地所需时间t1的多少倍?解:由题意得新知探究例7:电视塔越高,从塔顶发射出的电磁波传播得越远,从而能接收到电视节目信号的区域就越广. 已知
电视塔高h(km)与电视节目信号的传播半径r(km)之间满足 (其中R是地球半径).现有两座高分别为h1=400m, h2=450m的电视塔,问它们的传播半径之比等于多少?
新知探究因为解 设两座电视塔的传播半径分别为所以课堂小结商的算术平方根→计算与化简
→
最简二次根式↓↓→(逆用)课堂小测1.化简 的结果是( )
A.9 B.3 C. D. B2.下列根式中,最简二次根式是( )
A. B. C. D.C课堂小测3.若使等式 成立,则实数k取值范围是 ( )BA.k≥1 B.k≥2
C. 1<k≤2 D. 1≤k≤2 4.下列各式的计算中,结果为 的是( )
A. B.
C. D.C课堂小测5. 化简: 解:课堂小测6.在物理学中有公式W=I2Rt,其中W表示电功(单位:焦耳),I表示电流(单位:安培),R表示电阻(单位:欧姆),t表示时间(单位:秒),如果已知W,R,t,求I,则有 .若W=2400焦耳,R=100欧姆,t=15秒.试求电流I.解:当W=2400,R=100,t=15时,课堂小测7.自习课上,张玉看见同桌刘敏在练习本上写的题目是“求二次根式 中实数a的取值范围”,她告诉刘敏说:你把题目抄错了,不是“ ”,而是“ ”刘敏说:哎呀,真抄错了,好在不影响结果,反正a和a-3都在根号内.试问:刘敏说得对吗?解:刘敏说得不对,结果不一样.理由如下:
按 计算,则a≥0,a-3>0或a≤0,a-3<0,
解得a>3或a≤0;
而按 计算,则a≥0,a-3>0,
解得a>3.
1.理解二次根式的除法法则及商的算术平方根的性质.掌握最简二次根式的特点.(重点)
2.合理简洁地进行二次根式的除法运算.(难点)新课导入站在水平高度为h米的地方看见的水平距离为d米,它们近似地符合公式为 .解:问题1 某一登山者爬到海拔100米处,即 时,他看到的水平线的距离d1是多少?新知探究问题2 该登山者接着爬到海拔200米的山顶,即 时,此时他看到的水平线的距离d2是多少?问题3 他从海拔100米处登上海拔200米高的山顶,那么他看到的水平线的距离是原来的多少倍?解:二次根式的除法该怎样算呢?解:思考 乘法法则是如何得出的?除法有没有类似的法则?新知探究(1) ___÷___=____;= _____;计算下列各式:(2) ___÷___=____;(3) ___÷___=____;= _____;= _____.234567观察两者有什么关系? 新知探究观察三组式子的结果,我们得到下面三个等式:(1) (2) (3) 思考 通过上述二次根式除法运算的结果,联想到二次根式乘法运算法则,你能说出二次根式 的结果吗?特殊一般新知探究问题 在前面发现的规律 中,a,b的取值范围有没有限制呢?不对,同乘法法则一样,a,b都为非负数.a,b同号就可以啦!你们都错啦,a≥0,b>0,b=0时等式两边的二次根式就没有意义啦!新知探究归纳总结二次根式的商的算术平方根性质文字叙述:被开方数商的算术平方根等于算术平方根的商.当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得新知探究例1:化简下列二次根式.解: 从 变形到
是为了去掉分母中的根号.
化简二次根式时,最后结果一般要求分母中不含有二次根式.新知探究例2 化简:解:还有其他解法吗?补充解法:新知探究解:先应用商的算术平方根的性质,再运用积的平方根性质新知探究1.能使等式 成立的x的取值范围是( )
A.x≠2 B.x≥0 C.x>2 D.x≥2 C2.化简:解:新知探究我们可以运用它来进行二次根式的解题和化简.语言表述:积中各因式的算术平方根的商,等于商的算术平方根. 我们知道,把积的算术平方根的性质反过来就得到二次根式的乘法法则.类似的,把二次根式的商的算术平方根的性质反过来,就得到二次根式的除法法则:新知探究例3 计算: 新知探究例4 计算:解:除式是分数或分式时,先要转化为乘法再进行运算.新知探究解: 类似(4)中被开方数中含有带分数,应先将带分数化成假分数,再运用二次根式除法法则进行运算.
新知探究例5 设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.解:∵
∴新知探究例6 高空抛物现象被称为“悬在城市上空的痛”.据报道:一个30g的鸡蛋从18楼抛下来就可以砸破行人的头骨,从25楼抛下可以使人当场死亡.据研究从高空抛物时间t和高度h近似的满足公式 .从100米高空抛物到落地所需时间t2是从50米高空抛物到落地所需时间t1的多少倍?解:由题意得新知探究例7:电视塔越高,从塔顶发射出的电磁波传播得越远,从而能接收到电视节目信号的区域就越广. 已知
电视塔高h(km)与电视节目信号的传播半径r(km)之间满足 (其中R是地球半径).现有两座高分别为h1=400m, h2=450m的电视塔,问它们的传播半径之比等于多少?
新知探究因为解 设两座电视塔的传播半径分别为所以课堂小结商的算术平方根→计算与化简
→
最简二次根式↓↓→(逆用)课堂小测1.化简 的结果是( )
A.9 B.3 C. D. B2.下列根式中,最简二次根式是( )
A. B. C. D.C课堂小测3.若使等式 成立,则实数k取值范围是 ( )BA.k≥1 B.k≥2
C. 1<k≤2 D. 1≤k≤2 4.下列各式的计算中,结果为 的是( )
A. B.
C. D.C课堂小测5. 化简: 解:课堂小测6.在物理学中有公式W=I2Rt,其中W表示电功(单位:焦耳),I表示电流(单位:安培),R表示电阻(单位:欧姆),t表示时间(单位:秒),如果已知W,R,t,求I,则有 .若W=2400焦耳,R=100欧姆,t=15秒.试求电流I.解:当W=2400,R=100,t=15时,课堂小测7.自习课上,张玉看见同桌刘敏在练习本上写的题目是“求二次根式 中实数a的取值范围”,她告诉刘敏说:你把题目抄错了,不是“ ”,而是“ ”刘敏说:哎呀,真抄错了,好在不影响结果,反正a和a-3都在根号内.试问:刘敏说得对吗?解:刘敏说得不对,结果不一样.理由如下:
按 计算,则a≥0,a-3>0或a≤0,a-3<0,
解得a>3或a≤0;
而按 计算,则a≥0,a-3>0,
解得a>3.
同课章节目录
