2.3函数的奇偶性 课件(21张PPT)
文档属性
| 名称 | 2.3函数的奇偶性 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览






文档简介
课件21张PPT。函数的奇偶性北师大版必修一生活中的对称美新课引入:世博会中国馆故宫太和殿大门我们的校园现实生活中的“美” 我们发现现实生活中的许多事物都具有对称性,有的关于直线对称,有的关于点呈中心对称,那么在我们数学领域里,我们会研究函数图象的某对称性!xyoxyo 探究一 观察下列两个函数图象并思考以下问题:
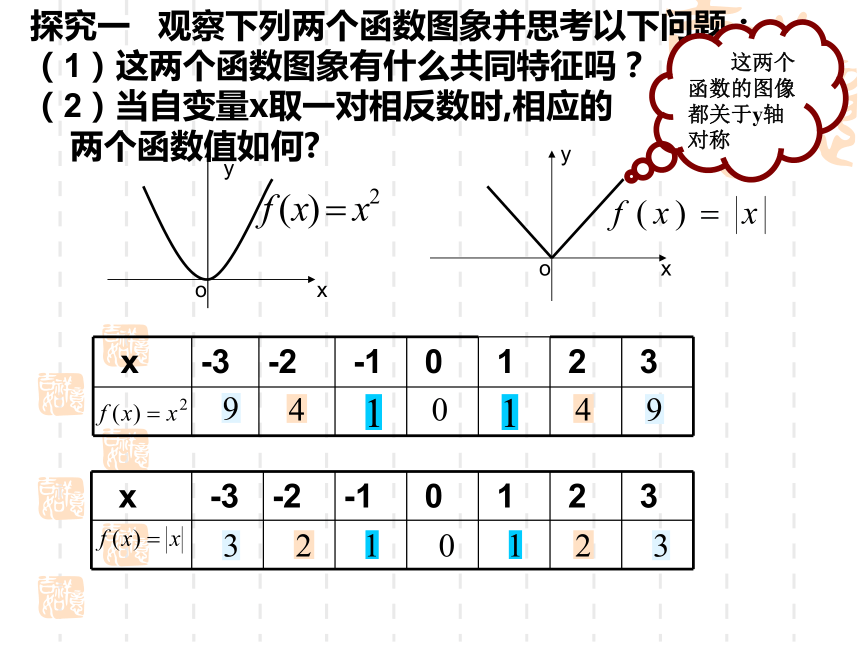
(1)这两个函数图象有什么共同特征吗?
(2)当自变量x取一对相反数时,相应的
两个函数值如何? 这两个函数的图像都关于y轴对称
从函数值对应表可以看到:
当自变量x取一对相反数时,相应的两个函数值相同对于f(x)=x2 ,f(-x)=(-x)2=x2 ,即f(-x)=f(x) 对于R内任意的一个x,都有f(-x) =f(x),这时我们称函数f(x)=x2 为偶函数.偶函数的概念: 如果对于函数f(x)的定义域内任意一个x,
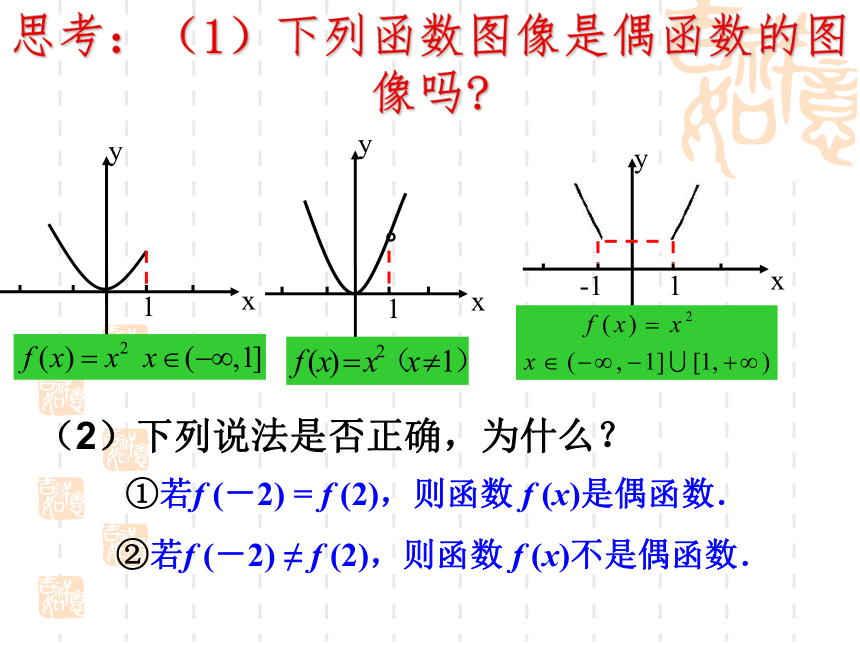
都有f(-x)= f(x),那么函数f(x)就叫做偶函数. 思考:定义中“任意一个x,都有f(-x)=f(x)成立”说明了什么? 说明f(-x)与f(x)都有意义,即-x、x必须同时属于定义域,因此偶函数的定义域关于原点对称的。思考:(1)下列函数图像是偶函数的图像吗?。 两个函数的图像都关于原点对称.探究二 观察下列两个函数图象并思考以下问题:
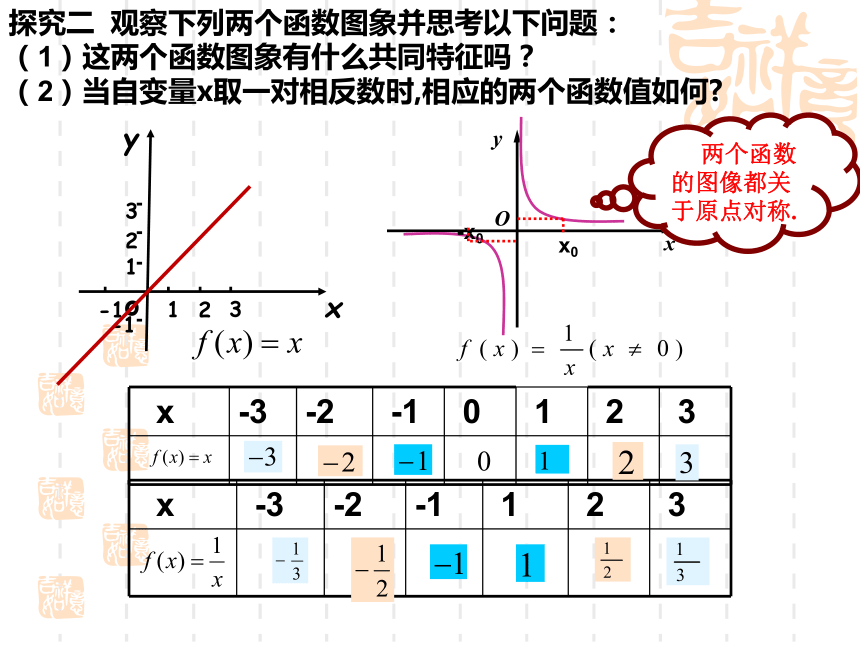
(1)这两个函数图象有什么共同特征吗?
(2)当自变量x取一对相反数时,相应的两个函数值如何?对于f(x)=x ,f(-x)= -x= -f(x) ,即f(-x)= -f(x). 对于R内任意的一个x,都有f(-x)= - f(x),这时我们称函数f(x)=x为奇函数.从函数值对应表可以看到:
当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数.奇函数的概念: 一般地,如果对于函数f(x)的定义域内的任意一个x,都有f(-x)= - f(x),那么称函数y=f(x)为奇函数.
(1) 定义域关于原点对称是函数具有奇偶性的先决条件。 对于奇、偶函数定义的几点说明:(2) 如果一个函数f(x)是奇函数或偶函数,
那么我们就说函数f(x)具有奇偶性.(3) 函数的奇偶性是函数的整体性质.奇偶性是对函数的整个定义域而言的.(2)偶函数的图象关于y轴对称. 这个函数为偶函数.奇偶函数图象的性质可用于:
① 判断函数的奇偶性.
②简化函数图象的画法(1)奇函数的图象关于原点对称. 这个函数为奇函数.奇、偶函数图象的性质:例1、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.例2.根据下列函数图象,判断函数奇偶性.
yxyxyx-12yx-11偶奇非奇
非偶奇图象法思考:如何判断一个函数的奇偶性呢?(1)图像法
(2)定义法例3.判断下列函数的奇偶性∴f(x)为奇函数.解:定义域为{x|x≠0},解:f(x)的定义域为{x|x≠0}.∴f(x)为偶函数.定义法用定义法判断函数奇偶性解题步骤:(1)先确定函数定义域,并判断
定义域是否关于原点对称;(2)求f(-x),找 f(-x)与f(x),-f(x)的关系;(3)作出结论:
若f(-x)= f(x),则f(x)是偶函数;
若f(-x)=-f(x),则f(x)是奇函数.课堂小结1.奇偶函数定义:
2. 图象性质:
奇函数?它的图象关于原点对称
偶函数?它的图象关于y 轴对称
3.判断奇偶性方法:图象法,定义法。4.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)与f(x)、-f(x)的关系;
③作出结论.小试牛刀:1.判断下列函数的奇偶性(1) f(x)=x3- 2x; (2) f(x)=2x4+3x2作业检测:一、填空:
1、如果对于函数f(x)的定义域内任意一个x,都有 那么函数
f(x)就叫做偶函数.
2、奇函数的图象关于 对称。
二、判断正误:
1、偶函数的图形不一定关于y轴对称…………( )
2、y=x 是奇函数………….…… ( )
三、判断下列函数的奇偶性
祝同学们学习进步!
(1)这两个函数图象有什么共同特征吗?
(2)当自变量x取一对相反数时,相应的
两个函数值如何? 这两个函数的图像都关于y轴对称
从函数值对应表可以看到:
当自变量x取一对相反数时,相应的两个函数值相同对于f(x)=x2 ,f(-x)=(-x)2=x2 ,即f(-x)=f(x) 对于R内任意的一个x,都有f(-x) =f(x),这时我们称函数f(x)=x2 为偶函数.偶函数的概念: 如果对于函数f(x)的定义域内任意一个x,
都有f(-x)= f(x),那么函数f(x)就叫做偶函数. 思考:定义中“任意一个x,都有f(-x)=f(x)成立”说明了什么? 说明f(-x)与f(x)都有意义,即-x、x必须同时属于定义域,因此偶函数的定义域关于原点对称的。思考:(1)下列函数图像是偶函数的图像吗?。 两个函数的图像都关于原点对称.探究二 观察下列两个函数图象并思考以下问题:
(1)这两个函数图象有什么共同特征吗?
(2)当自变量x取一对相反数时,相应的两个函数值如何?对于f(x)=x ,f(-x)= -x= -f(x) ,即f(-x)= -f(x). 对于R内任意的一个x,都有f(-x)= - f(x),这时我们称函数f(x)=x为奇函数.从函数值对应表可以看到:
当自变量x取一对相反数时,相应的函数值f(x)也是一对相反数.奇函数的概念: 一般地,如果对于函数f(x)的定义域内的任意一个x,都有f(-x)= - f(x),那么称函数y=f(x)为奇函数.
(1) 定义域关于原点对称是函数具有奇偶性的先决条件。 对于奇、偶函数定义的几点说明:(2) 如果一个函数f(x)是奇函数或偶函数,
那么我们就说函数f(x)具有奇偶性.(3) 函数的奇偶性是函数的整体性质.奇偶性是对函数的整个定义域而言的.(2)偶函数的图象关于y轴对称. 这个函数为偶函数.奇偶函数图象的性质可用于:
① 判断函数的奇偶性.
②简化函数图象的画法(1)奇函数的图象关于原点对称. 这个函数为奇函数.奇、偶函数图象的性质:例1、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.例2.根据下列函数图象,判断函数奇偶性.
yxyxyx-12yx-11偶奇非奇
非偶奇图象法思考:如何判断一个函数的奇偶性呢?(1)图像法
(2)定义法例3.判断下列函数的奇偶性∴f(x)为奇函数.解:定义域为{x|x≠0},解:f(x)的定义域为{x|x≠0}.∴f(x)为偶函数.定义法用定义法判断函数奇偶性解题步骤:(1)先确定函数定义域,并判断
定义域是否关于原点对称;(2)求f(-x),找 f(-x)与f(x),-f(x)的关系;(3)作出结论:
若f(-x)= f(x),则f(x)是偶函数;
若f(-x)=-f(x),则f(x)是奇函数.课堂小结1.奇偶函数定义:
2. 图象性质:
奇函数?它的图象关于原点对称
偶函数?它的图象关于y 轴对称
3.判断奇偶性方法:图象法,定义法。4.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)与f(x)、-f(x)的关系;
③作出结论.小试牛刀:1.判断下列函数的奇偶性(1) f(x)=x3- 2x; (2) f(x)=2x4+3x2作业检测:一、填空:
1、如果对于函数f(x)的定义域内任意一个x,都有 那么函数
f(x)就叫做偶函数.
2、奇函数的图象关于 对称。
二、判断正误:
1、偶函数的图形不一定关于y轴对称…………( )
2、y=x 是奇函数………….…… ( )
三、判断下列函数的奇偶性
祝同学们学习进步!
