2.3 映射 课件(23张PPT)
图片预览








文档简介
课件23张PPT。2.3 映射通过丰富的实例,理解映射的概念.(重点)
了解像与原像的概念.
正确理解映射与函数的关系.(难点)日常生活中存在着丰富的对应关系.
请思考并分析下面给出的对应关系,它们有什么共同特点?2.集合A={中国,美国,英国,日本},B={北京,东京,华盛顿,伦敦},对应关系是:对于集合A中的每一个国家,在集合B中都有一个首都与它对应.1.集合A={全班同学},集合B={全班同学的姓},对应关系是:集合A中的每一个同学在集合B中都有一个属于自己的姓.3.设集合A={0,-3,2,3,-1,-2,1 },
集合B={9,0,4,1,5},对应关系是:集合A中的每一个数,在集合B中都有其对应的平方数.(2)对于集合A中的每一个元素在集合B中的对应元素是唯一的.三个对应关系的共同特点:(1)集合A中的每一个元素在集合B中都有对应元素;映射的概念 像这样,两个非空集合A与B间存在着对应关系f,而且对于A中的每一个元素x,B中总有唯一的一个元素y与它对应,就称这种对应为从A到B的映射,记作
f:A→B
A中的元素x称为原像,B中的对应元素y称为x的像,1.函数与映射有什么区别与联系?(1)函数是一种特殊的映射;
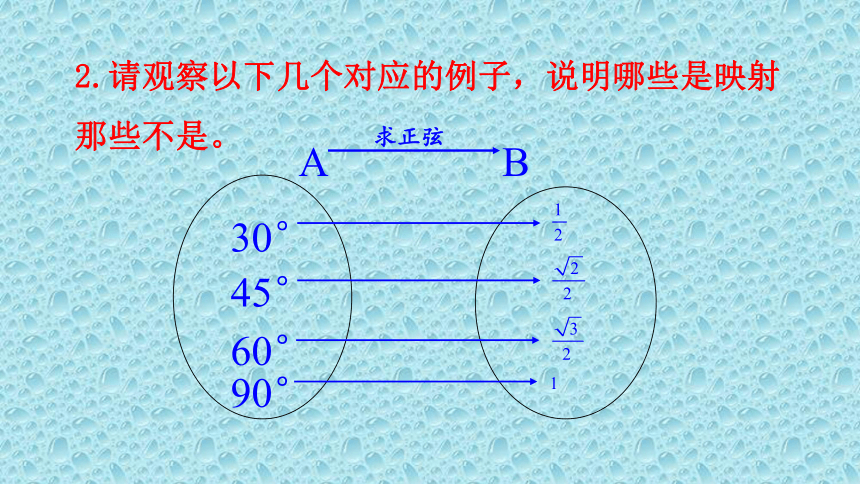
(2)两个集合中的元素类型有区别; 2.请观察以下几个对应的例子,说明哪些是映射那些不是。求正弦3
-32
-21
-1941AB求平方9413
-32
-21
-1不是映射AB求平方根1
2
3
4
5
6
1
2
3AB乘以2
4
12
200
1
2
3
4
5不是映射AB乘以4映射f:A→B,可理解为以下四点:1.A中每一个元素在B中都有唯一的像与之对应.2.对A中不同的元素,在B中可以有相同的像.3.允许B中元素没有原像.4.A中元素与B中元素的对应关系,可以是:一对一,多对一,但不能一对多. 在实际中,我们经常使用一种特殊的映射,通常叫作一一映射.它满足:1.A中每一个元素在B中都有唯一的像与之对应;
2.A中的不同元素的像也不同;
3.B中的每一个元素都有原像. 函数是一种特殊的映射,是从非空数集到非空数集的映射.
函数概念可以叙述为:设A,B是两个非空数集,f是A到B的一个映射,那么映射f:A→B叫作A到B的函数.
在函数中,原像的集合称为定义域,像的集合称为值域.说明 在研究实际问题的过程中,人们通常通过编号等方式(如风、海浪、地震等的级别)把一般映射数字化,使之成为函数,因为一旦表示为函数,那么有关函数的性质以及函数值的运算就都可以使用了.解:(1)点(2,3)在映射f下的像是(1,7);(2)点(4,6)在映射f下的原像是(2.5,1).1. (2012·菏泽高一检测)点(x,y)在映射f下的像是 (2x-y,2x+y),
(1)求点(2,3)在映射f下的像;
(2)求点(4,6)在映射f下的原像.2.判断下列对应是否为映射?a
b
ce
f
ga
b
c
de
f
ga
b
ce
f
g
d是是不是3. 下面的对应哪些是从A到B的映射,哪些不是? (1)A={0,1,2…},B={0,1,2},对应关系f:A中的元素对应它除以3的余数;
(2)A={平面上的点}, ,对应关系f:A中的元素对应它在平面上的坐标;
(3)A=R,B=R,对应关系f: 是是不是4.把下列两个集合间的对应关系用映射符号(如,
f:A→B)表示.其中,哪些是一一映射?哪些是函数?
(1)A={你们班的同学} ,B={体重},f:每个同学对应自己的体重;
(2)M={1,2,3,4},N={2,4,6,8},f:n=2m,n∈N,m∈M.
(3)X=R,Y={非负实数},f:y=x4,x∈X,y∈Y.函数函数不是一一映射映射的概念.
像与原像的概念.
映射与函数的关系.生活中没有什么可怕的东西,只有需要理解的东西。
——居里夫人
了解像与原像的概念.
正确理解映射与函数的关系.(难点)日常生活中存在着丰富的对应关系.
请思考并分析下面给出的对应关系,它们有什么共同特点?2.集合A={中国,美国,英国,日本},B={北京,东京,华盛顿,伦敦},对应关系是:对于集合A中的每一个国家,在集合B中都有一个首都与它对应.1.集合A={全班同学},集合B={全班同学的姓},对应关系是:集合A中的每一个同学在集合B中都有一个属于自己的姓.3.设集合A={0,-3,2,3,-1,-2,1 },
集合B={9,0,4,1,5},对应关系是:集合A中的每一个数,在集合B中都有其对应的平方数.(2)对于集合A中的每一个元素在集合B中的对应元素是唯一的.三个对应关系的共同特点:(1)集合A中的每一个元素在集合B中都有对应元素;映射的概念 像这样,两个非空集合A与B间存在着对应关系f,而且对于A中的每一个元素x,B中总有唯一的一个元素y与它对应,就称这种对应为从A到B的映射,记作
f:A→B
A中的元素x称为原像,B中的对应元素y称为x的像,1.函数与映射有什么区别与联系?(1)函数是一种特殊的映射;
(2)两个集合中的元素类型有区别; 2.请观察以下几个对应的例子,说明哪些是映射那些不是。求正弦3
-32
-21
-1941AB求平方9413
-32
-21
-1不是映射AB求平方根1
2
3
4
5
6
1
2
3AB乘以2
4
12
200
1
2
3
4
5不是映射AB乘以4映射f:A→B,可理解为以下四点:1.A中每一个元素在B中都有唯一的像与之对应.2.对A中不同的元素,在B中可以有相同的像.3.允许B中元素没有原像.4.A中元素与B中元素的对应关系,可以是:一对一,多对一,但不能一对多. 在实际中,我们经常使用一种特殊的映射,通常叫作一一映射.它满足:1.A中每一个元素在B中都有唯一的像与之对应;
2.A中的不同元素的像也不同;
3.B中的每一个元素都有原像. 函数是一种特殊的映射,是从非空数集到非空数集的映射.
函数概念可以叙述为:设A,B是两个非空数集,f是A到B的一个映射,那么映射f:A→B叫作A到B的函数.
在函数中,原像的集合称为定义域,像的集合称为值域.说明 在研究实际问题的过程中,人们通常通过编号等方式(如风、海浪、地震等的级别)把一般映射数字化,使之成为函数,因为一旦表示为函数,那么有关函数的性质以及函数值的运算就都可以使用了.解:(1)点(2,3)在映射f下的像是(1,7);(2)点(4,6)在映射f下的原像是(2.5,1).1. (2012·菏泽高一检测)点(x,y)在映射f下的像是 (2x-y,2x+y),
(1)求点(2,3)在映射f下的像;
(2)求点(4,6)在映射f下的原像.2.判断下列对应是否为映射?a
b
ce
f
ga
b
c
de
f
ga
b
ce
f
g
d是是不是3. 下面的对应哪些是从A到B的映射,哪些不是? (1)A={0,1,2…},B={0,1,2},对应关系f:A中的元素对应它除以3的余数;
(2)A={平面上的点}, ,对应关系f:A中的元素对应它在平面上的坐标;
(3)A=R,B=R,对应关系f: 是是不是4.把下列两个集合间的对应关系用映射符号(如,
f:A→B)表示.其中,哪些是一一映射?哪些是函数?
(1)A={你们班的同学} ,B={体重},f:每个同学对应自己的体重;
(2)M={1,2,3,4},N={2,4,6,8},f:n=2m,n∈N,m∈M.
(3)X=R,Y={非负实数},f:y=x4,x∈X,y∈Y.函数函数不是一一映射映射的概念.
像与原像的概念.
映射与函数的关系.生活中没有什么可怕的东西,只有需要理解的东西。
——居里夫人
