北师大版必修一第二章第二节函数的概念 课件(21张PPT)
文档属性
| 名称 | 北师大版必修一第二章第二节函数的概念 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览







文档简介
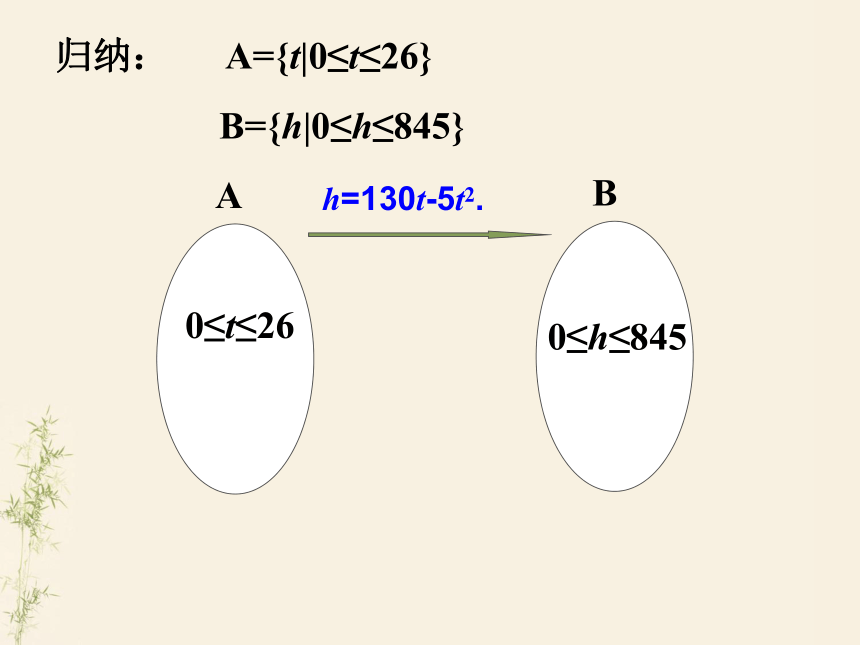
课件21张PPT。1.请同学们回忆在初中我们学过那些函数? 答:正比例函数:y =kx (k≠0) ;复习回顾反比例函数:一次函数:y =kx+b (k≠0) 二次函数:y =ax2+bx+c (a≠0) 一般地,设在一个变化过程中有两个变量x、y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。2.什么是函数(传统定义)2.2函数的概念A={t|0≤t≤26}B={h|0≤h≤845}问题情境(1)一枚炮弹发射后,经过26 s落到地面击中
目标. 炮弹的射高为845 m,且炮弹距地面的
高度(单位: m)随时间t (单位: s)变化的规律
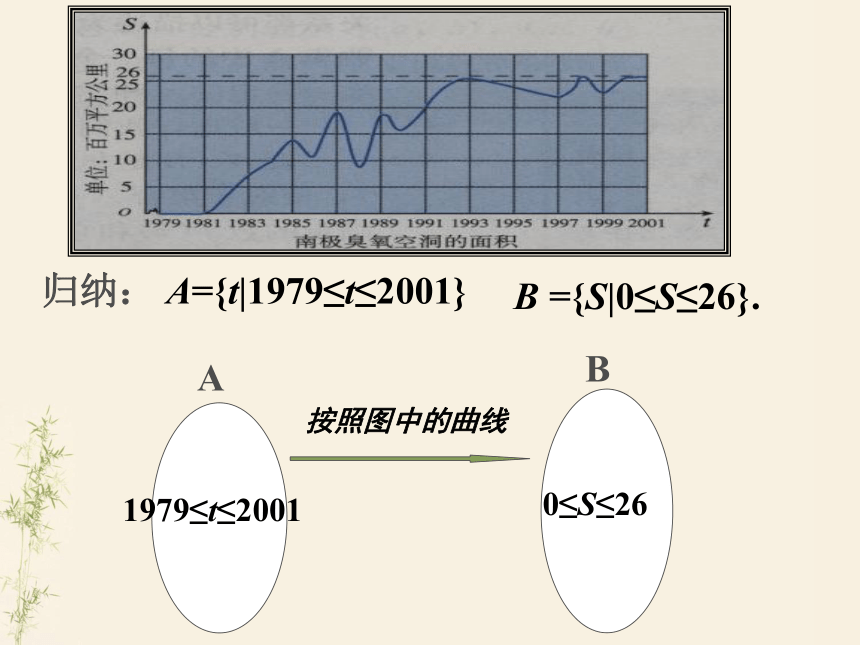
是h=130t-5t2.归纳: A={t|0≤t≤26} B={h|0≤h≤845}0≤t≤260≤h≤845ABh=130t-5t2.(2) 近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.下图中的曲线显示了南极上空臭氧空洞的面积从1979~2001年的变化情况:归纳: A={t|1979≤t≤2001} 1979≤t≤20010≤S≤26AB按照图中的曲线 B ={S|0≤S≤26}.“八五”计划以来城镇居民家庭恩格尔系数变化情况(3)国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.下表中恩格尔系数随时间(年)变化的情况表明, “八五”计划以来我国城镇居民的生活质量发生了显著变化.
归纳:A={1991,1992,1993,1994,…,2001}B={53.8%,52.9%,50.1 %, …,39.2%,37.9 %}1991,1992,
1993,1994,
…
200153.8%,
52.9%,
…
37.9 %AB按照表格 以上三个实例的共同特点是: 对于数集A中的每一个x,按照某种对应关系f,在数集B中都有唯一的y和它对应.归纳总结函数近代定义:构建概念(1)给定两个非空数集A和B;
(2)如果按照某个对应关系f;
(3)对于集合A中任何一个数x,在集合B中都存在唯一确定的数f(x)与之对应;把满足以上条件的对应关系f叫作定义在集合A上的函数。记作:?:A→B或y=f(x),x A 此时, x叫做自变量, 集合A叫做函数的定义域集合{f(x)|x∈A}叫做函数的值域。函数定义:构建概念(1)给定两个非空数集A和B;
(2)如果按照某个对应关系f;
(3)对于集合A中任何一个数x,在集合B中都存在唯一确定的数f(x)与之对应;把满足以上条件的对应关系f叫作定义在集合A上的函数。记作:?:A→B或y=f(x),x A 此时, x叫做自变量, 集合A叫做函数的定义域集合{f(x)|x∈A}叫做函数的值域。概念理解:(1) 两种概念本质一致,表述角度的不同而已;
(2)“非空数集” 的两种理解;
(3)函数的本质核心,对应法则f的理解;
(4)函数的三要素:定义域、对应法则、值域;
(5)同一函数的概念;定义域相同,对应法则相同;
(6)两个变量的三性:任意性,存在性,唯一性;
(7)可以 是一对一或多对一,但不能是一对多;例1:下列对应关系能否构成定义在A上的函数1
2
3ABf4
5
61
2
3A4
61
2
3A4
5
6
7BBff1
2
3ABf4
5
61
2
3A4
5
61
2
3中国
美国
英国BBff(1)(2)(3)(4)(5)(6)A典例讲解不是不是练一练2.下列图像具有函数关系的是:( )ADCBE练一练yoxxyo 例2:下面函数中,哪个与函数 y = x 是同一个函数?(1)定义域不合题意:{x|x≥ 0};(2)定义域不合题意:{x|x≠0};(4)对应法则不合题意: y = |x|.只需看其定义域和对应关系是否一致.(3)y = x 定义域为R,满足题意;例:3.求下列函数的定义域:定义域为 R定义域为{x|x≠-1}
使函数解析式有意义的自变量的一切值;
定义域为 收获感悟 1.函数定义及理解3.求函数定义域
使函数解析式有意义的自变量的一切值;
2.函数的三要素:定义域、值域、对应关系.4.抽象与概括5.数形结合
2、课后思考:
常见函数式子的表示形式,以及对自变量的取值要求。谢谢!
目标. 炮弹的射高为845 m,且炮弹距地面的
高度(单位: m)随时间t (单位: s)变化的规律
是h=130t-5t2.归纳: A={t|0≤t≤26} B={h|0≤h≤845}0≤t≤260≤h≤845ABh=130t-5t2.(2) 近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.下图中的曲线显示了南极上空臭氧空洞的面积从1979~2001年的变化情况:归纳: A={t|1979≤t≤2001} 1979≤t≤20010≤S≤26AB按照图中的曲线 B ={S|0≤S≤26}.“八五”计划以来城镇居民家庭恩格尔系数变化情况(3)国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.下表中恩格尔系数随时间(年)变化的情况表明, “八五”计划以来我国城镇居民的生活质量发生了显著变化.
归纳:A={1991,1992,1993,1994,…,2001}B={53.8%,52.9%,50.1 %, …,39.2%,37.9 %}1991,1992,
1993,1994,
…
200153.8%,
52.9%,
…
37.9 %AB按照表格 以上三个实例的共同特点是: 对于数集A中的每一个x,按照某种对应关系f,在数集B中都有唯一的y和它对应.归纳总结函数近代定义:构建概念(1)给定两个非空数集A和B;
(2)如果按照某个对应关系f;
(3)对于集合A中任何一个数x,在集合B中都存在唯一确定的数f(x)与之对应;把满足以上条件的对应关系f叫作定义在集合A上的函数。记作:?:A→B或y=f(x),x A 此时, x叫做自变量, 集合A叫做函数的定义域集合{f(x)|x∈A}叫做函数的值域。函数定义:构建概念(1)给定两个非空数集A和B;
(2)如果按照某个对应关系f;
(3)对于集合A中任何一个数x,在集合B中都存在唯一确定的数f(x)与之对应;把满足以上条件的对应关系f叫作定义在集合A上的函数。记作:?:A→B或y=f(x),x A 此时, x叫做自变量, 集合A叫做函数的定义域集合{f(x)|x∈A}叫做函数的值域。概念理解:(1) 两种概念本质一致,表述角度的不同而已;
(2)“非空数集” 的两种理解;
(3)函数的本质核心,对应法则f的理解;
(4)函数的三要素:定义域、对应法则、值域;
(5)同一函数的概念;定义域相同,对应法则相同;
(6)两个变量的三性:任意性,存在性,唯一性;
(7)可以 是一对一或多对一,但不能是一对多;例1:下列对应关系能否构成定义在A上的函数1
2
3ABf4
5
61
2
3A4
61
2
3A4
5
6
7BBff1
2
3ABf4
5
61
2
3A4
5
61
2
3中国
美国
英国BBff(1)(2)(3)(4)(5)(6)A典例讲解不是不是练一练2.下列图像具有函数关系的是:( )ADCBE练一练yoxxyo 例2:下面函数中,哪个与函数 y = x 是同一个函数?(1)定义域不合题意:{x|x≥ 0};(2)定义域不合题意:{x|x≠0};(4)对应法则不合题意: y = |x|.只需看其定义域和对应关系是否一致.(3)y = x 定义域为R,满足题意;例:3.求下列函数的定义域:定义域为 R定义域为{x|x≠-1}
使函数解析式有意义的自变量的一切值;
定义域为 收获感悟 1.函数定义及理解3.求函数定义域
使函数解析式有意义的自变量的一切值;
2.函数的三要素:定义域、值域、对应关系.4.抽象与概括5.数形结合
2、课后思考:
常见函数式子的表示形式,以及对自变量的取值要求。谢谢!
