二次函数在区间上的最值问题 课件(32张PPT)
文档属性
| 名称 | 二次函数在区间上的最值问题 课件(32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 15:23:16 | ||
图片预览



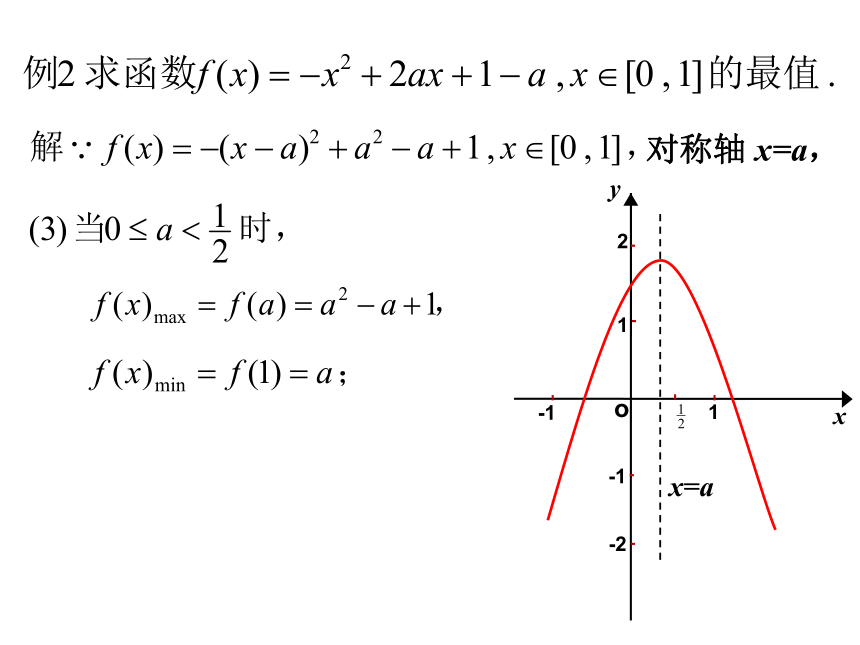


文档简介
课件32张PPT。二次函数在区间上的最值问题北师大2003课标版
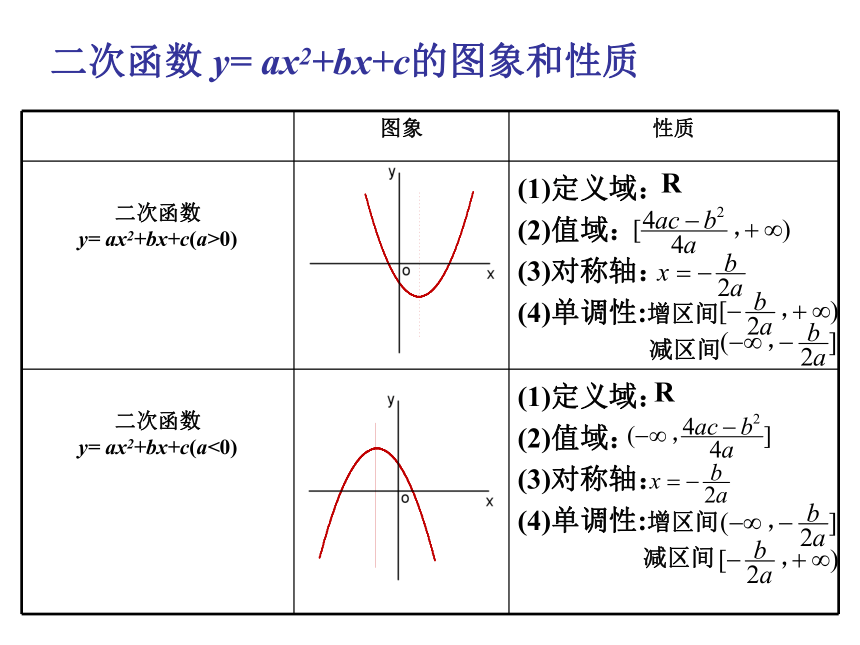
高中数学二次函数 y= ax2+bx+c的图象和性质RR例1 已知函数 f(x) = -x2 + 2x + 3 ,分别求函数在下列区间的最值.
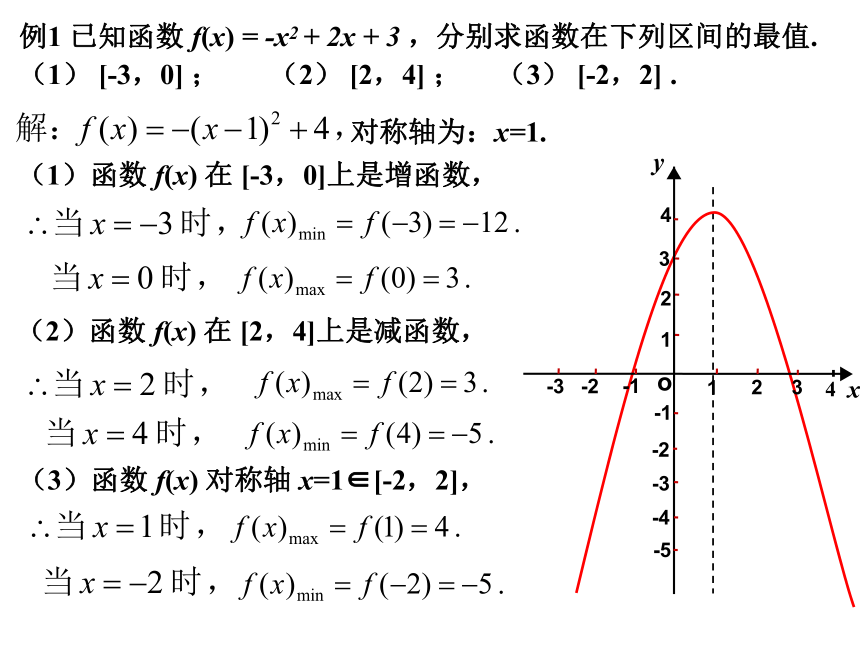
(1) [-3,0] ; (2) [2,4] ; (3) [-2,2] .
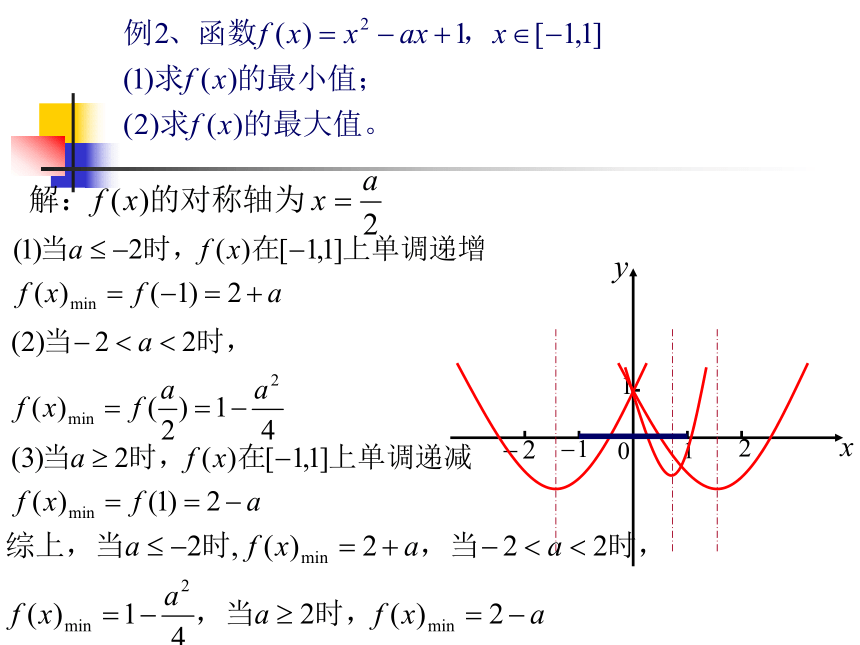
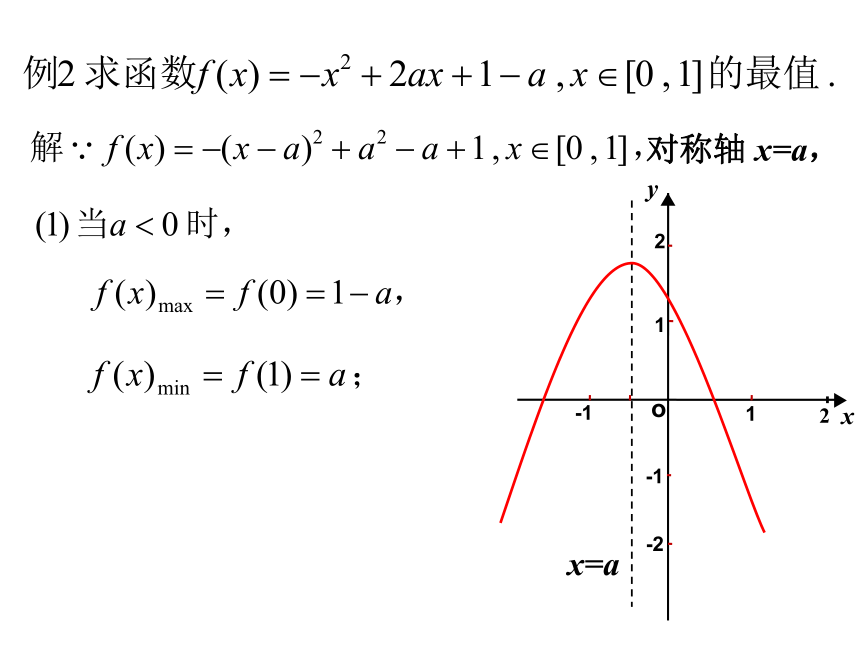
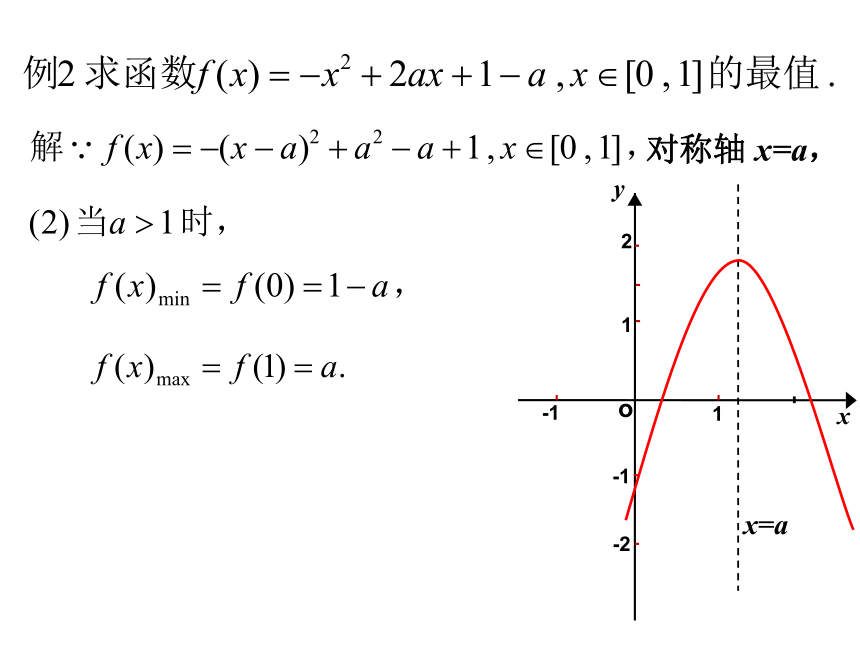
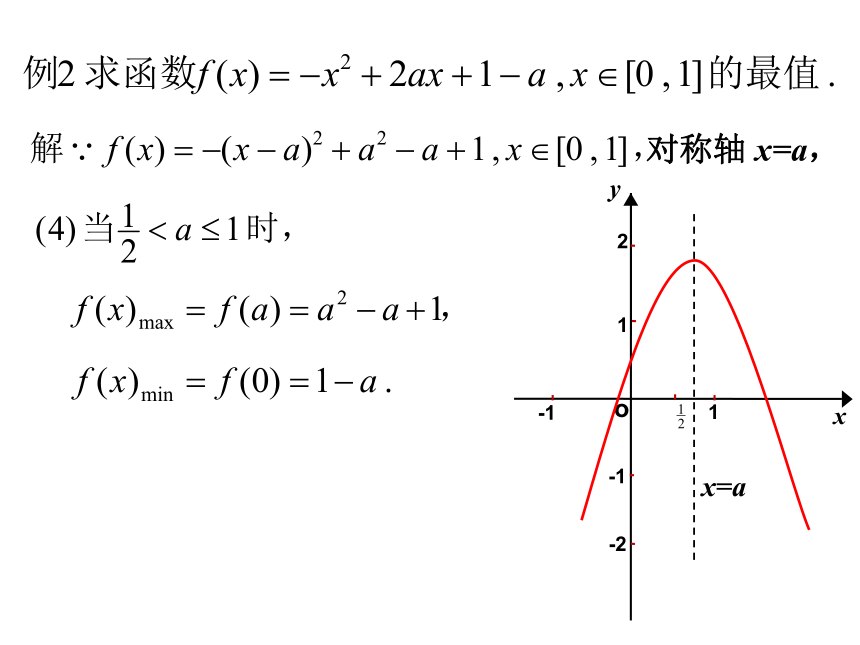
对称轴为:x=1.(1)函数 f(x) 在 [-3,0]上是增函数,(2)函数 f(x) 在 [2,4]上是减函数,(3)函数 f(x) 对称轴 x=1∈[-2,2], 二次函数 y= ax2+bx+c 在区间 [m,n]上的最值问题,一般情况下,按对称轴与区间的关系分三种情况讨论求解.说 明:x=a对称轴 x=a,对称轴 x=a,对称轴 x=a,对称轴 x=a,解:则对称轴 x=m,无解,综上所述:解法2:例4、若关于x的方程3x2-5x+a=0的一根大于-2而小于0,另一根大于1而小于3,试求实数a 的取值范围。例5、已知关于x的方程4x2-4x+m=0在[-1,1]上
有两个根,求m的取值范围。例6、若关于x的方程2kx2-2x-3k-2=0的两根一个小于1,另一根大于1,试求实数k 的取值范围。一、若关于x的方程ax2 +bx + c=0,(a>0)的一个根在 (m,n),另一根在(p,q),求a,b,c满足的条件。类型一:二、若关于x的方程ax2 +bx + c=0(a>0)的两个根都在 (m,n),求a,b,c满足的条件。类型二:二、若关于x的方程ax2 +bx + c=0(a>0)的两个根,一个根大于k,一个根小于k,求a,b,c满足的条件。类型二:作 业:解:综上所述:,则解:f(x)对称轴 x=a,综上所述:1. 设函数 的定义域为[t-2,t-1],对任意t∈R,求函数f(x)的最小值g(t)的解析式,并画出其图象.练 习:34-82 .某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
?
(I)写出图一表示的市场售价与时间的函数关系式P=f(t);
写出图二表示的种植成本与时间的函数关系式Q=g(t);
(II)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/102kg,时间单位:天) 解:(I)由图一可得市场售价与时间的函数关系为
由图二可得种植成本与时间的函数关系为 (II)设t时刻的纯收益为h(t),则由题意得 h(t)=f(t)-g(t)
即
当0≤t≤200时,配方整理得当 20087.5可知, h(t)在区间[0,300]上可以取最大值100,此时,t=50 ,即从二月一日开始的第50天时,上市的西红柿纯收益最大。 所以,当t=50时,h(t)取得区间[0 ,200]上的最大值100;所以,当t=300时,h(t)取得区间[200,300]上的最大值87.5
高中数学二次函数 y= ax2+bx+c的图象和性质RR例1 已知函数 f(x) = -x2 + 2x + 3 ,分别求函数在下列区间的最值.
(1) [-3,0] ; (2) [2,4] ; (3) [-2,2] .
对称轴为:x=1.(1)函数 f(x) 在 [-3,0]上是增函数,(2)函数 f(x) 在 [2,4]上是减函数,(3)函数 f(x) 对称轴 x=1∈[-2,2], 二次函数 y= ax2+bx+c 在区间 [m,n]上的最值问题,一般情况下,按对称轴与区间的关系分三种情况讨论求解.说 明:x=a对称轴 x=a,对称轴 x=a,对称轴 x=a,对称轴 x=a,解:则对称轴 x=m,无解,综上所述:解法2:例4、若关于x的方程3x2-5x+a=0的一根大于-2而小于0,另一根大于1而小于3,试求实数a 的取值范围。例5、已知关于x的方程4x2-4x+m=0在[-1,1]上
有两个根,求m的取值范围。例6、若关于x的方程2kx2-2x-3k-2=0的两根一个小于1,另一根大于1,试求实数k 的取值范围。一、若关于x的方程ax2 +bx + c=0,(a>0)的一个根在 (m,n),另一根在(p,q),求a,b,c满足的条件。类型一:二、若关于x的方程ax2 +bx + c=0(a>0)的两个根都在 (m,n),求a,b,c满足的条件。类型二:二、若关于x的方程ax2 +bx + c=0(a>0)的两个根,一个根大于k,一个根小于k,求a,b,c满足的条件。类型二:作 业:解:综上所述:,则解:f(x)对称轴 x=a,综上所述:1. 设函数 的定义域为[t-2,t-1],对任意t∈R,求函数f(x)的最小值g(t)的解析式,并画出其图象.练 习:34-82 .某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
?
(I)写出图一表示的市场售价与时间的函数关系式P=f(t);
写出图二表示的种植成本与时间的函数关系式Q=g(t);
(II)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/102kg,时间单位:天) 解:(I)由图一可得市场售价与时间的函数关系为
由图二可得种植成本与时间的函数关系为 (II)设t时刻的纯收益为h(t),则由题意得 h(t)=f(t)-g(t)
即
当0≤t≤200时,配方整理得当 200
