2.3.函数单调性的应用(求最值) 课件(19张PPT)
文档属性
| 名称 | 2.3.函数单调性的应用(求最值) 课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 15:23:56 | ||
图片预览




文档简介
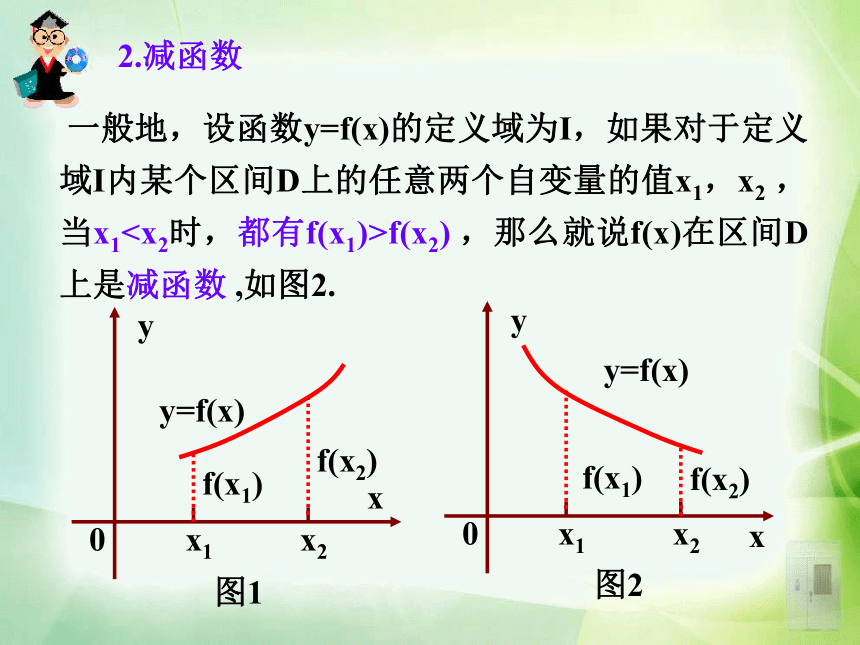
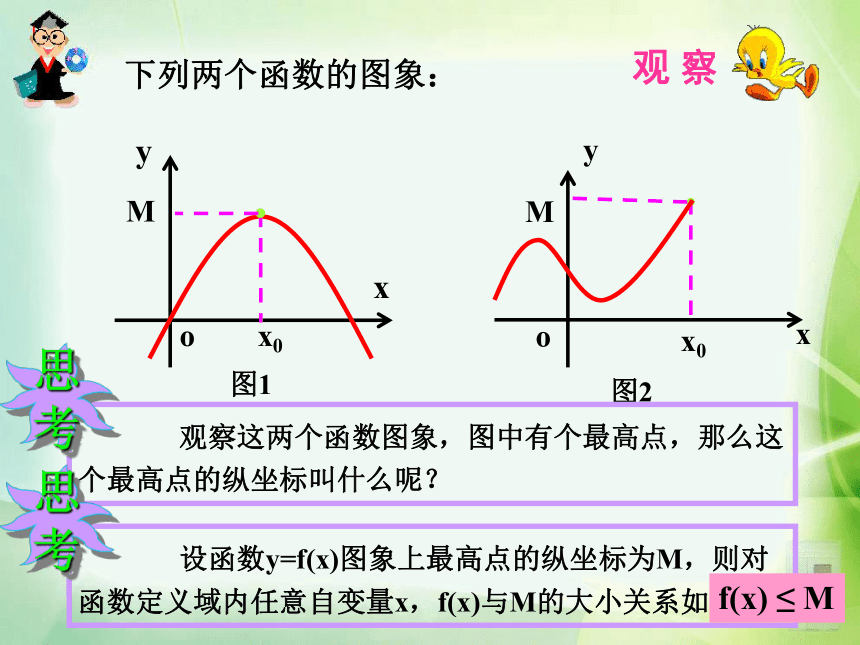
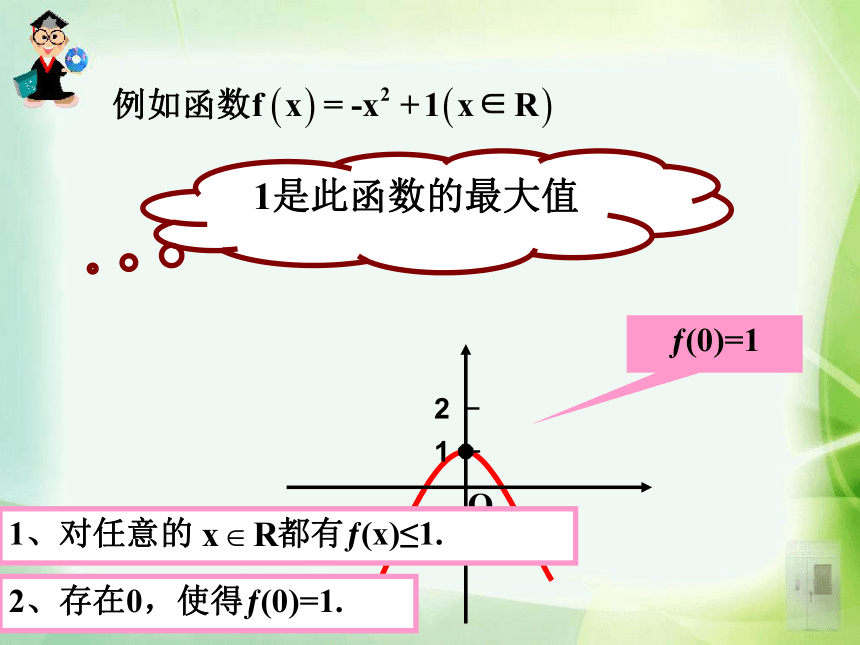
课件19张PPT。1.3.1 第二课时函数的最大(小)值回顾函数单调性的概念: 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2 ,当x1f(x2) ,那么就说f(x)在区间D上是减函数 ,如图2.下列两个函数的图象: 观 察f(x) ≤ M?(0)=12、存在0,使得?(0)=1.1、对任意的 都有?(x)≤1.1是此函数的最大值知识要点M是函数y= f (x)的最大值(maximum value): 一般地,设函数y= f (x)的定义域为I,如果存在实数M满足:
(1)对于任意的x ∈I,都有f (x) ≤M;
(2)存在 ,使得 .
那么,我们称M是函数y= f (x)的最大值 一般地,设函数y=f(x)的定义域为I,如果实数M满足:
(1)对于任意的的x∈I,都有f(x) ≥M;
(2)存在 ,使得 ,
那么我们称M是函数y=f(x)的最小值(minimun value).函数f(x)在定义域中既有最大值又有最小值.值域是[a,b]探究:函数单调性与函数的最值的关系(1)若函数y=f (x)在区间[m,n] (m做出函数 的图像。显然,函数图像的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度. 所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.方法二配方法
对函数配方得h(t)=-4.9 +29.025当 t=1.5时,函数有最大值h ≈29 所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.例5 已知函数 ,求函数的最大值与最小. 分析:由函数的图象可知道,此函数在[3,5]上递减。所以在区间[3,5]的两个端点上分别取得最大值与最小值. 解:设 是区间[3,5]上的任意两个实数,且 ,则课堂练习 课堂小结 2、函数的最值的求法(1)利用二次函数的性质(配方法)求函数的最值;
(2)利用图象求函数的最值;
(3)利用函数单调性求函数的最值 .1、函数的最值的概念
(1)对于任意的x ∈I,都有f (x) ≤M;
(2)存在 ,使得 .
那么,我们称M是函数y= f (x)的最大值 一般地,设函数y=f(x)的定义域为I,如果实数M满足:
(1)对于任意的的x∈I,都有f(x) ≥M;
(2)存在 ,使得 ,
那么我们称M是函数y=f(x)的最小值(minimun value).函数f(x)在定义域中既有最大值又有最小值.值域是[a,b]探究:函数单调性与函数的最值的关系(1)若函数y=f (x)在区间[m,n] (m
对函数配方得h(t)=-4.9 +29.025当 t=1.5时,函数有最大值h ≈29 所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.例5 已知函数 ,求函数的最大值与最小. 分析:由函数的图象可知道,此函数在[3,5]上递减。所以在区间[3,5]的两个端点上分别取得最大值与最小值. 解:设 是区间[3,5]上的任意两个实数,且 ,则课堂练习 课堂小结 2、函数的最值的求法(1)利用二次函数的性质(配方法)求函数的最值;
(2)利用图象求函数的最值;
(3)利用函数单调性求函数的最值 .1、函数的最值的概念
