2.3函数的单调性 课件(31张PPT)
文档属性
| 名称 | 2.3函数的单调性 课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 398.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 15:21:24 | ||
图片预览





文档简介
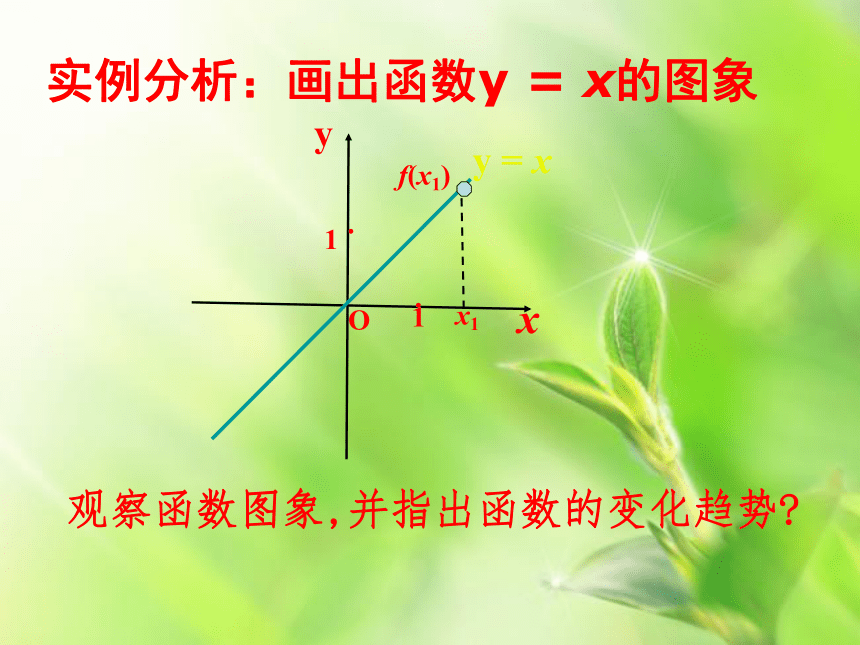
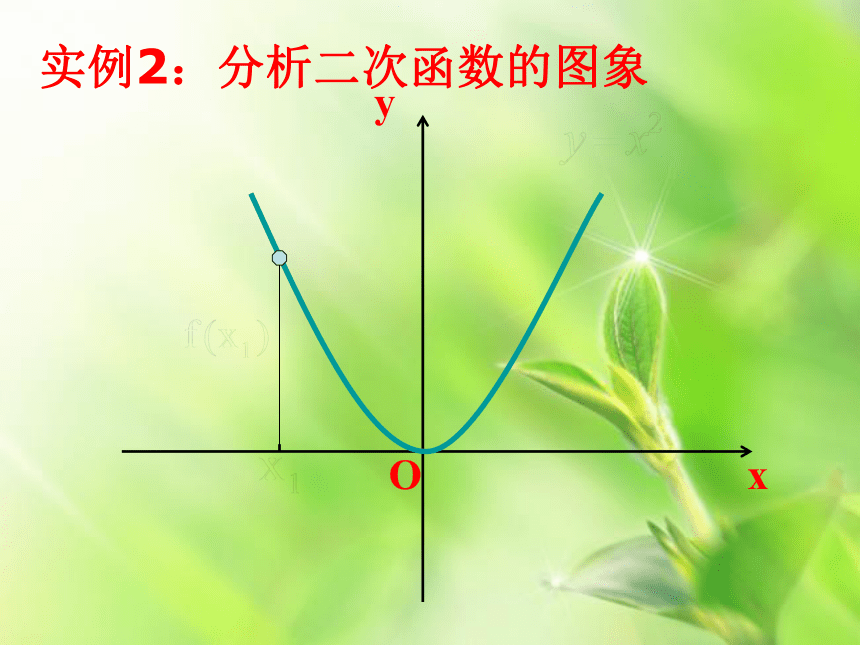
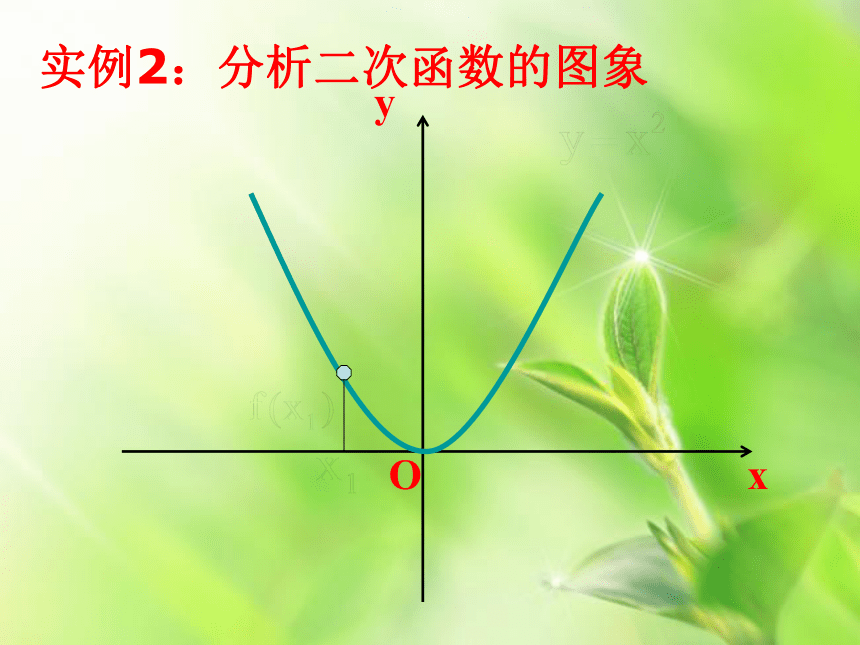
课件31张PPT。函数的单调性能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?局部上升或下降下降上升xyy = xO11··引例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?f(x1)x1xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象函数的这种性质称为函数的单调性对区间I内 x1,x2 ,
当x1当x1当x1MN任意两个自变量的值x1,x2,区间I内随着x的增大,y也增大图象在区间I逐渐上升I 那么就说在f(x)这个区间上是单调
减函数,I称为f(x)的单调 减 区间.类比单调增函数的研究方法定义单调减函数.x 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 那么就说在f(x)这个区间上是单调增 函数,I称为f(x)的单调 区间.增当x1单调区间(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。思考:(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。注意:判断2:定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;(3) x 1, x 2 取值的任意性123-2-3-2-1o-4-1y-1.5[-1.5,3],[5,6][-4,-1.5],[3,5],[6,7]例2.画出下列函数图像,并写出单调区间:数缺形时少直观,例2.画出下列函数图像,并写出单调区间:描点作图练一练 小结
1.函数单调性的定义中有哪些关键点?
2.判断函数单调性有哪些常用方法?
3.你学会了哪些数学思想方法?
当x1
减函数,I称为f(x)的单调 减 区间.类比单调增函数的研究方法定义单调减函数.x 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 如果对于属于定义域A内某个区间I上
的任意两个自变量的值x1,x2, 那么就说在f(x)这个区间上是单调增 函数,I称为f(x)的单调 区间.增当x1
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。思考:(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
在单调区间上,增函数的图象是上升的,减函数的图象是下降的。注意:判断2:定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;(3) x 1, x 2 取值的任意性123-2-3-2-1o-4-1y-1.5[-1.5,3],[5,6][-4,-1.5],[3,5],[6,7]例2.画出下列函数图像,并写出单调区间:数缺形时少直观,例2.画出下列函数图像,并写出单调区间:描点作图练一练 小结
1.函数单调性的定义中有哪些关键点?
2.判断函数单调性有哪些常用方法?
3.你学会了哪些数学思想方法?
