2.3函数的单调性 课件(25张PPT)
文档属性
| 名称 | 2.3函数的单调性 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 15:26:07 | ||
图片预览





文档简介
课件25张PPT。必修一函数的单调性
(1) y=x (2) y=-x
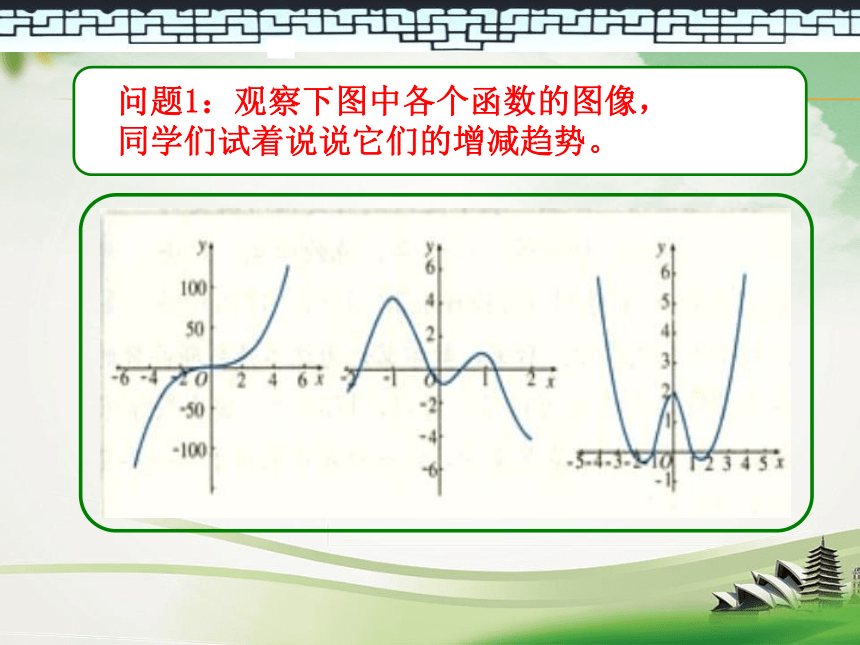
(3) y=|x| (4) y=x2下面请同学们做出下列函数的图像。 问题1:观察下图中各个函数的图像,
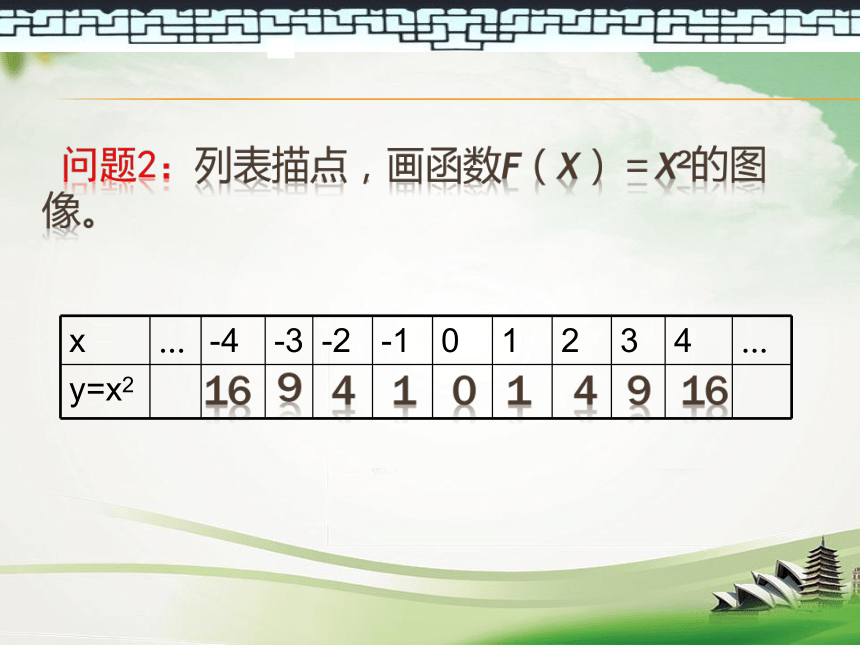
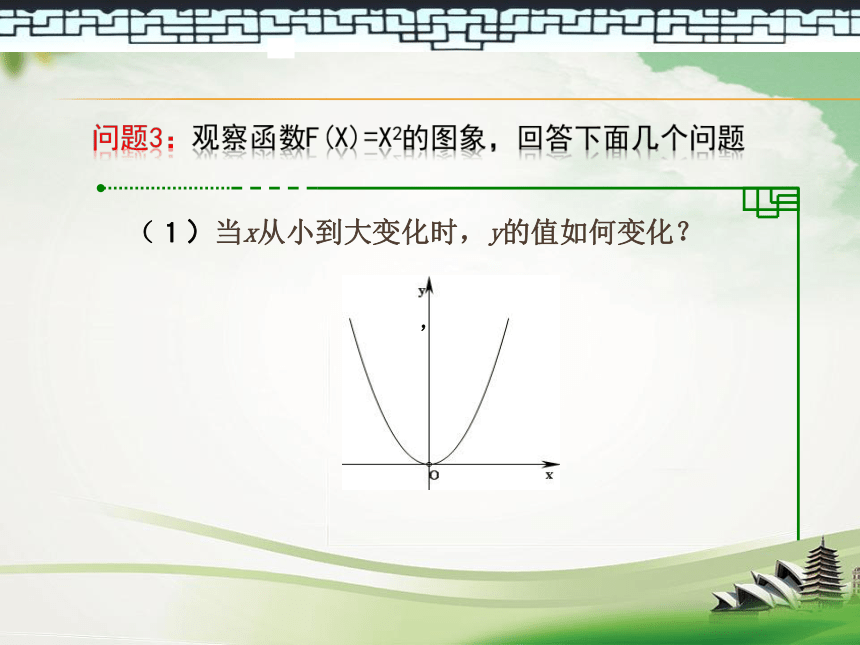
同学们试着说说它们的增减趋势。 问题2:列表描点,画函数f(x)=x2的图像。 16410149916 问题3:观察函数f(x)=x2的图象,回答下面几个问题 (1)当x从小到大变化时,y的值如何变化?
, 问题3:观察函数f(x)=x2的图象,回答下面几个问题(2)?比较下列各数的大小。
22,32,42,4.52,5.12,6.32。
由图可知:22<32<42<4.52<5.12<6.32。
显然有:当0<x1<x2<x3<x4<x5<x6时,
0<y1<y2<y3<y4<y5<y6。
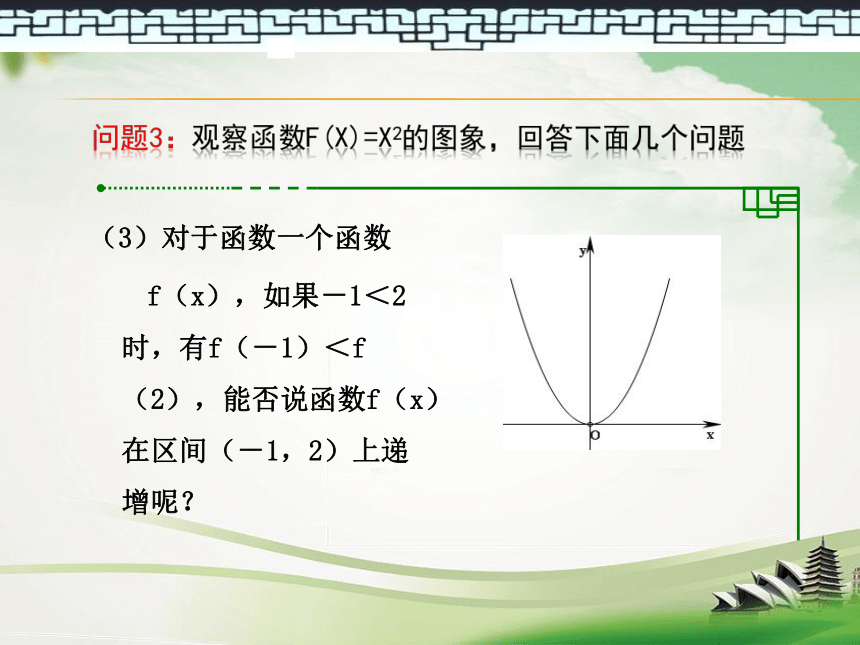
, 问题3:观察函数f(x)=x2的图象,回答下面几个问题(3)对于函数一个函数
f(x),如果-1<2时,有f(-1)<f(2),能否说函数f(x)在区间(-1,2)上递增呢?
问题4:函数f(x),对于(0,∞)上的两个自变量的值x1,x2,当0<x1<x2时,有0<y1<y2,能否说函数f(x)在(0,+∞)上递增呢?请画图说明。
问题5:函数f(x),对于(0,∞)上的三个自变量的值x1,x2,x3,当0<x1<x2<x3时,有0<y1<y2<y3,能否说函数f(x)在(0,+∞)上递增呢?请画图说明。
问题6:函数f(x),对于(0,∞)上的无数个自变量的值x1,x2,x3,当0<x1<x2<x3<…时,有0<y1<y2<y3<…,能否说函数f(x)在(0,+∞)上递增呢?请画图说明。
问题7:你能否举出一个具体的函数的例子,使得它在区间(-∞,+∞)上,对任意x1<x2,总有y1<y2。
问题8:你能否举出一个具体函数的例子,使得它在区间(0,+∞)上,对任意x1<x2,总有y1>y2。
在区间A上,若随着自变量的增大函数值也增大,则称函数在区间A上是增加的;在区间A上,若随着自变量的增大函数值减少,则称函数在区间A上是减少的.同学们尝试描述一下函数的单调性 同样地,在区间(-∞,0]上,任取x1 ,x2 ,
当 x1 f(x2) ,这时称函数f(x)=x2在区间(-∞,0]上是减少的. 对函数f(x)= x2,在区间[0,+∞)上,任取x1 ,x2 ,当 x1 f(x)= 解: (-∞,0)和
(0,+∞)都是函数的单调区间,在 这两个区间上函数f(x)=1/x 是减少的。 例3 画出函数 f(x)=3x +2的图像,判断它的单调性,并加以证明。 f(x)= 解 :作出f(x)=3x +2的图像。又图看出函数
f(x)的图像在R上是上升的,函数 f(x)是R
上的增函数。 总结步骤:取值 作差判断变形4.回顾反思 深化认知 (1)通过增(减)函数概念的形成过程,你学 到了什么?
(3)怎样用定义证明函数的单调性?(2)如何根据图象指出函数的单调区间?作业:课本P39 A组 2(1)(2)(3)(4)谢 谢
(1) y=x (2) y=-x
(3) y=|x| (4) y=x2下面请同学们做出下列函数的图像。 问题1:观察下图中各个函数的图像,
同学们试着说说它们的增减趋势。 问题2:列表描点,画函数f(x)=x2的图像。 16410149916 问题3:观察函数f(x)=x2的图象,回答下面几个问题 (1)当x从小到大变化时,y的值如何变化?
, 问题3:观察函数f(x)=x2的图象,回答下面几个问题(2)?比较下列各数的大小。
22,32,42,4.52,5.12,6.32。
由图可知:22<32<42<4.52<5.12<6.32。
显然有:当0<x1<x2<x3<x4<x5<x6时,
0<y1<y2<y3<y4<y5<y6。
, 问题3:观察函数f(x)=x2的图象,回答下面几个问题(3)对于函数一个函数
f(x),如果-1<2时,有f(-1)<f(2),能否说函数f(x)在区间(-1,2)上递增呢?
问题4:函数f(x),对于(0,∞)上的两个自变量的值x1,x2,当0<x1<x2时,有0<y1<y2,能否说函数f(x)在(0,+∞)上递增呢?请画图说明。
问题5:函数f(x),对于(0,∞)上的三个自变量的值x1,x2,x3,当0<x1<x2<x3时,有0<y1<y2<y3,能否说函数f(x)在(0,+∞)上递增呢?请画图说明。
问题6:函数f(x),对于(0,∞)上的无数个自变量的值x1,x2,x3,当0<x1<x2<x3<…时,有0<y1<y2<y3<…,能否说函数f(x)在(0,+∞)上递增呢?请画图说明。
问题7:你能否举出一个具体的函数的例子,使得它在区间(-∞,+∞)上,对任意x1<x2,总有y1<y2。
问题8:你能否举出一个具体函数的例子,使得它在区间(0,+∞)上,对任意x1<x2,总有y1>y2。
在区间A上,若随着自变量的增大函数值也增大,则称函数在区间A上是增加的;在区间A上,若随着自变量的增大函数值减少,则称函数在区间A上是减少的.同学们尝试描述一下函数的单调性 同样地,在区间(-∞,0]上,任取x1 ,x2 ,
当 x1
(0,+∞)都是函数的单调区间,在 这两个区间上函数f(x)=1/x 是减少的。 例3 画出函数 f(x)=3x +2的图像,判断它的单调性,并加以证明。 f(x)= 解 :作出f(x)=3x +2的图像。又图看出函数
f(x)的图像在R上是上升的,函数 f(x)是R
上的增函数。 总结步骤:取值 作差判断变形4.回顾反思 深化认知 (1)通过增(减)函数概念的形成过程,你学 到了什么?
(3)怎样用定义证明函数的单调性?(2)如何根据图象指出函数的单调区间?作业:课本P39 A组 2(1)(2)(3)(4)谢 谢
