2.5简单的幂函数 课件(23张PPT)
文档属性
| 名称 | 2.5简单的幂函数 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 00:00:00 | ||
图片预览







文档简介
课件23张PPT。 简单的幂函数教学目标1.了解幂函数的概念;能够通过观察总结简单幂函数的一些性质;会利用定义判断或证明简单函数的奇偶性。
2.了解利用奇偶性画函数图像和研究函数的方法。
3.培养从特殊归纳出一般的意识,培养利用图像研究函数奇偶性的能力,引导学生发现数学中的对称美。
教学重点:幂函数的概念;奇偶函数的概念
教学难点:简单幂函数的图像、性质;正确判断函数的奇偶性。19:472 我们学过一次函数,二次函数,反比例函数
如它们在形式上有什么异同? 相同:函数解析式是幂的形式,且指数是常数,
底数是自变量.
不同:指数不同 一般地,如果一个函数,底数是自变量x,指数是常量 a ,即 y=xa ,这样的函数叫做幂函数.
注意:幂函数中的指数 a可以为任意实数.在中学阶段我们只关注a=1,2,3,-1,1/2
一.幂函数1.幂函数概念2.幂函数的特征:(1) y=xa的系数是1 ;(2) 底数为x而不是x的代数式,如2x或x-2等;(3) 幂函数y=xa中指数a确定则幂函数确定。练习:
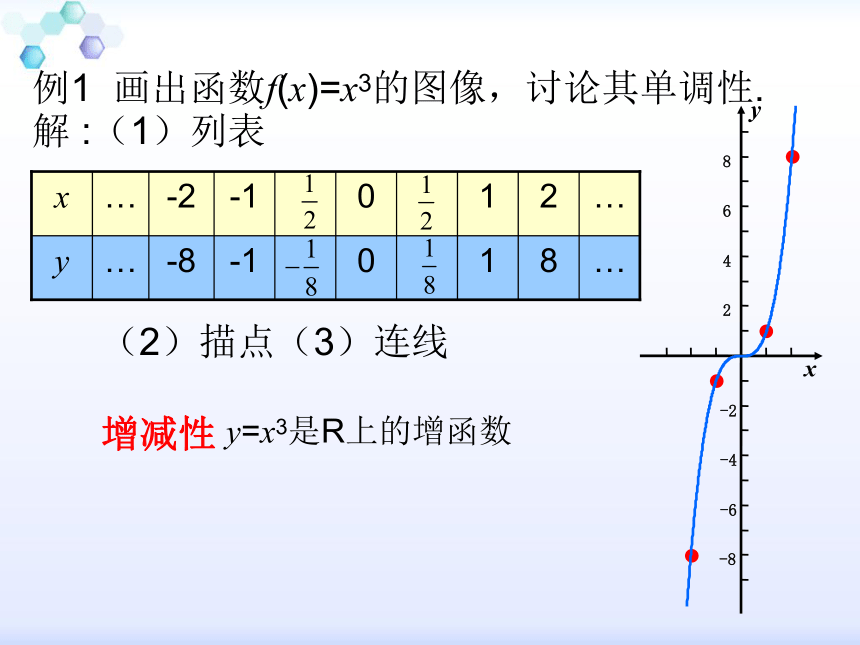
1.判断下列函数是否为幂函数.2.幂函数y=f(x)的图像过点(2,8),求函数的解析式.答案:y=x3例1 画出函数f(x)=x3的图像,讨论其单调性.y=x3是R上的增函数(2)描点(3)连线
增减性
学生活动:
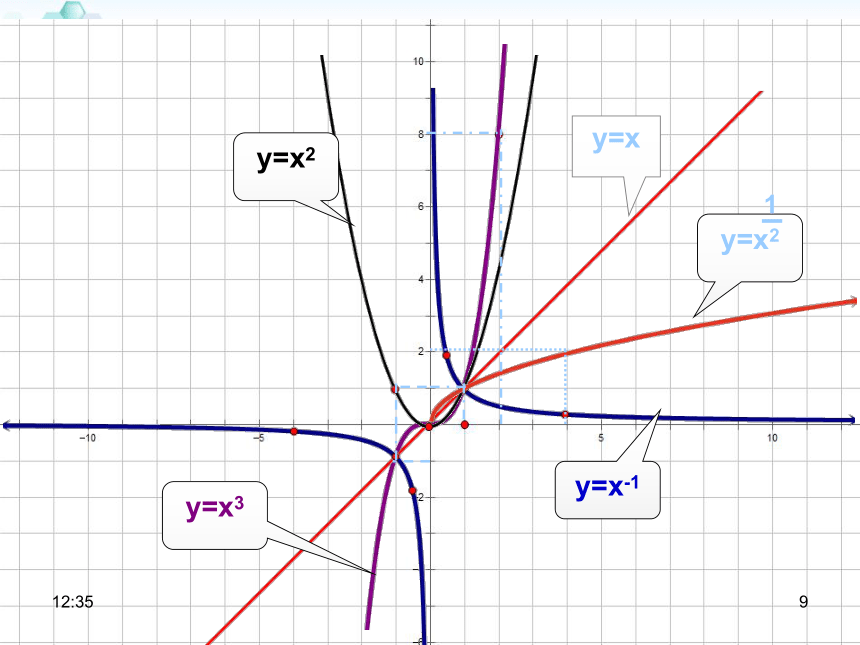
请在同一坐标系中画出
的图像,观察图像特别是第一象限的特征,你有何发现?y=x3y=xy=x2y=x-119:479基础
梳理(1,1)(0,0)和(1,1)递增递减练习:比较下列三个值的大小0.20.3 ,0.30.3 ,0.30.2解:①先比较0.20.3,0.30.3 的大小考察y=x0.3在区间(0,+ ∞)上为增函数因为 0.2<0.3所以 0.20.3<0.30.3②再比较0.30.3,0.30.2的大小考察y=0.3x所以在R上为减函数因为 0.3>0.2所以 0.30.3<0.30.2所以 0.20.3 < 0.30.3 < 0.30.219:4711思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系? xyo三.函数的奇偶性奇函数定义:
一般地,图像关于原点
对称的函数叫作奇函数 在奇函数中,f(-x)和 f(x)的绝对值相等,符号相反,即f(-x)= - f(x)结论:函数f(x)=x3 的图像关于原点对称。(1)观察f(x)=x3的图象 偶函数定义:
一般地,图像关于y轴对称的函数叫作偶函数.xyo-xxf(-x)思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系? f(-x)= f(x)(2)观察函数f(x)=x2图像 在偶函数中, f(-x)和f(x)的值
相等,即
结论:函数f(x)=x2 的图像关于y轴对称。☆对奇函数、偶函数定义的说明:(1) 函数具有奇偶性的前提是:定义域关于原点对称。 (2) 若f(-x)=-f(x),则f(x)为奇函数, 反之亦然。
若f(-x)= f(x) ,则f(x)为偶函数, 反之亦然。(3) 当函数f(x)是奇函数或偶函数时,称函数具有奇偶性。例2 判断f(x)=-2x5和g(x)=x4+2的奇偶性.解 因为在R上f(x)=-2x5,f(-x)=-2(-x)5=2x5,所以
f(x)=-f(-x),
于是f(x)是奇函数.
而g(x)=x4+2,g(-x)=(-x)4+2=x4+2,所以
g(x)=g(-x).
于是g(x)是偶函数.想一想:已知函数f(x)是定义域为R的偶函数,在(-?,0]上的图象如图,你能试作出[0,+?)内的图象吗?想一想:已知函数f(x)是定义在R上的奇函数,在(-?,0]上的图象如图,你能试作出 [0,+?)内的图象。练习1.判断下列函数的奇偶性:方法一:根据函数的图象,判断其奇偶性.奇函数非奇非偶偶函数非奇非偶方法二根据定义,判断其奇偶性.自测
自评 栏目链接3.下图中,只画出了函数图像的一半,请你画出它们的另一半,并说出画法的依据.小结幂函数奇函数偶函数图像关于原点对称图像关于y轴对称奇偶性
2.了解利用奇偶性画函数图像和研究函数的方法。
3.培养从特殊归纳出一般的意识,培养利用图像研究函数奇偶性的能力,引导学生发现数学中的对称美。
教学重点:幂函数的概念;奇偶函数的概念
教学难点:简单幂函数的图像、性质;正确判断函数的奇偶性。19:472 我们学过一次函数,二次函数,反比例函数
如它们在形式上有什么异同? 相同:函数解析式是幂的形式,且指数是常数,
底数是自变量.
不同:指数不同 一般地,如果一个函数,底数是自变量x,指数是常量 a ,即 y=xa ,这样的函数叫做幂函数.
注意:幂函数中的指数 a可以为任意实数.在中学阶段我们只关注a=1,2,3,-1,1/2
一.幂函数1.幂函数概念2.幂函数的特征:(1) y=xa的系数是1 ;(2) 底数为x而不是x的代数式,如2x或x-2等;(3) 幂函数y=xa中指数a确定则幂函数确定。练习:
1.判断下列函数是否为幂函数.2.幂函数y=f(x)的图像过点(2,8),求函数的解析式.答案:y=x3例1 画出函数f(x)=x3的图像,讨论其单调性.y=x3是R上的增函数(2)描点(3)连线
增减性
学生活动:
请在同一坐标系中画出
的图像,观察图像特别是第一象限的特征,你有何发现?y=x3y=xy=x2y=x-119:479基础
梳理(1,1)(0,0)和(1,1)递增递减练习:比较下列三个值的大小0.20.3 ,0.30.3 ,0.30.2解:①先比较0.20.3,0.30.3 的大小考察y=x0.3在区间(0,+ ∞)上为增函数因为 0.2<0.3所以 0.20.3<0.30.3②再比较0.30.3,0.30.2的大小考察y=0.3x所以在R上为减函数因为 0.3>0.2所以 0.30.3<0.30.2所以 0.20.3 < 0.30.3 < 0.30.219:4711思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系? xyo三.函数的奇偶性奇函数定义:
一般地,图像关于原点
对称的函数叫作奇函数 在奇函数中,f(-x)和 f(x)的绝对值相等,符号相反,即f(-x)= - f(x)结论:函数f(x)=x3 的图像关于原点对称。(1)观察f(x)=x3的图象 偶函数定义:
一般地,图像关于y轴对称的函数叫作偶函数.xyo-xxf(-x)思考:函数图象上横坐标互为相反数的点的纵坐标有什么关系? f(-x)= f(x)(2)观察函数f(x)=x2图像 在偶函数中, f(-x)和f(x)的值
相等,即
结论:函数f(x)=x2 的图像关于y轴对称。☆对奇函数、偶函数定义的说明:(1) 函数具有奇偶性的前提是:定义域关于原点对称。 (2) 若f(-x)=-f(x),则f(x)为奇函数, 反之亦然。
若f(-x)= f(x) ,则f(x)为偶函数, 反之亦然。(3) 当函数f(x)是奇函数或偶函数时,称函数具有奇偶性。例2 判断f(x)=-2x5和g(x)=x4+2的奇偶性.解 因为在R上f(x)=-2x5,f(-x)=-2(-x)5=2x5,所以
f(x)=-f(-x),
于是f(x)是奇函数.
而g(x)=x4+2,g(-x)=(-x)4+2=x4+2,所以
g(x)=g(-x).
于是g(x)是偶函数.想一想:已知函数f(x)是定义域为R的偶函数,在(-?,0]上的图象如图,你能试作出[0,+?)内的图象吗?想一想:已知函数f(x)是定义在R上的奇函数,在(-?,0]上的图象如图,你能试作出 [0,+?)内的图象。练习1.判断下列函数的奇偶性:方法一:根据函数的图象,判断其奇偶性.奇函数非奇非偶偶函数非奇非偶方法二根据定义,判断其奇偶性.自测
自评 栏目链接3.下图中,只画出了函数图像的一半,请你画出它们的另一半,并说出画法的依据.小结幂函数奇函数偶函数图像关于原点对称图像关于y轴对称奇偶性
