2.5简单的幂函数 课件(38张PPT)
文档属性
| 名称 | 2.5简单的幂函数 课件(38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 508.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 15:25:36 | ||
图片预览











文档简介
课件38张PPT。2.5简单的幂函数 (1)如果张红购买了每千克1元的蔬菜w千克,那么她需要支付P = ______
w 元(2)如果正方形的边长为 a,那么正方形的面积S = ____(3)如果立方体的边长为a,那么立方体的体积V = ____
(5)如果某人 t s内骑车行进1 km,那么他骑车的平均速度v=__________
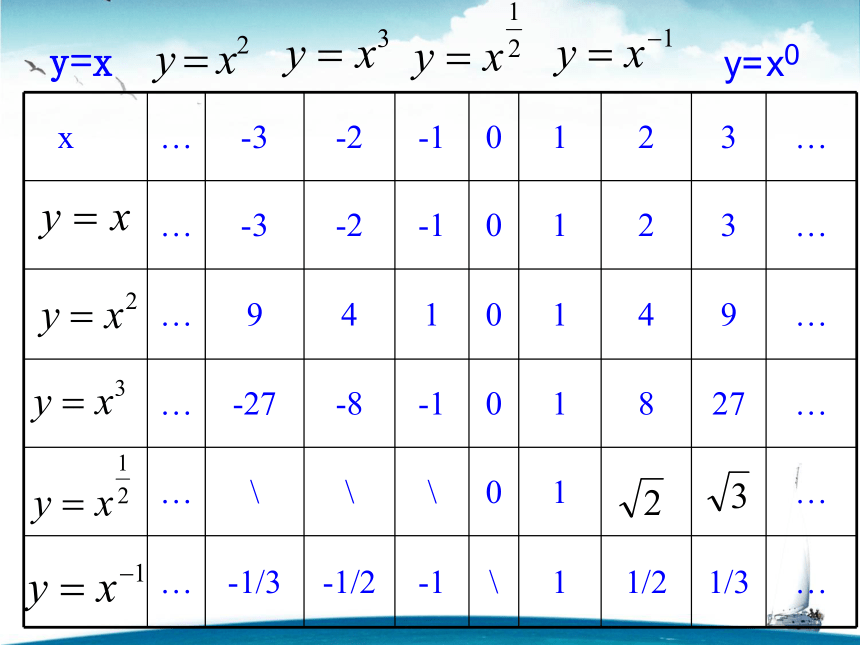
____是____的函数a2 a3 V是a的函数t?1 km/s v是t 的函数(4)如果一个正方形场地的面积为 S,那么正方形的边长 a= _________a是S的函数以上问题中的函数具有什么共同特征?Pwy=xy=x2y=x3y=xy=x-1____是____的函数Sa知识回顾:一般的形如:y= xα (α R)的函数我们叫做幂函数,其中x是自变量,α是常数 幂函数定义域随指数α的不同而不同,未知数x是底数
(在中学阶段只关注α=1,2,3,1/2,-1这几种情形)指数为常数底数为自变量1探究新知:单项式练习1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
(5) y=x2 +2 (6) y=-x3我是例1 画出函数f(x)=x3的图像,讨论其单调性xyoy=x3--||11-1-1y=x3是R上的增函数大家还有什么发现?函数的图象关于原点对称对于任意x,都有f(-x)=-f(x)一般地,奇函数的图象关于原点对称,反过来,如果一个函数的图象关于原点对称,那么这个函数是奇函数。课堂典例讲练:对于函数y=x2呢?y=x2xy-1大家有什么类似发现?函数的图象关于y轴对称偶函数的图象关于y轴对称,反过来,如果一个函数的图象关于y轴对称,那么这个函数是偶函数 oy对于任意x,都有f(-x)=f(x)探究新知 (1)如果对于函数f(x)定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.
(2)如果对于函数f(x)定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数
如果函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性 函数的奇偶性判断方法:
法一:图像法
法二:定义法:(如下)步骤一:判断函数的定义域是否关于原点对称,如果对称进行步骤二,否则不具有奇偶性步骤二:归纳升华:例2 判断函数(1)f(x)= -2x5
(2)g(x)=x4+2
(3)h(x)=x4+2(x>0)的奇偶性 课堂典例讲练:加
油补全下面四个函数的图像动手实践下面研究幂函数在同一平面直角坐标系内作出这
六个幂函数的图象.
结合图象,研究性质:定义域、值域、单调性、奇偶性、过定点的情况等。研究 y=x知识提升:y=xxyoRR奇函数在R上
是增函数[0,+∞)在[0,+∞)上增,在[0,+∞)上增,R偶函数RR奇函数在R上
是增函数[0,+∞)[0,+∞)在[0,+∞)上增,非奇非
偶函数{x|x≠0}{y|y≠0}在(-∞,0)上减,在(0,+∞)上减奇函数奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当α>0时,图象随x增大而上升。
当α<0时,图象随x增大而下降
思维升华:图象都经过哪个定点?在第一象限内:
当a>0时,图象随x增大而上升,函数是增加的。
当a<0时,图象随x增大而下降,函数是减少的。图象都经过点(1,1)x=1a>0时,图象还都过点(0,0)点x=1右侧:图高指大幂函数在第四象限都没有图像练习: 如图所示,曲线是幂函数 y = xa在第一象限内的图象,已知 a分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1
的右侧,大指数在上,小指数在下,
在Y轴与直线x =1之间正好相反。 1C4C2C3C1
如果函数 是幂函数,且在区间(0,+∞)内是减少的,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1当 m=2时,函数为
当m=-1时,函数为因为m=-1不合题意,所以m=2即
m {m|m=2}知识巩固:
解:(1)y= x0.8在(0,+∞)内是增加的,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x-2/5在(0,+∞)内是减少的,
∵2.5<2.7∴ 2.5-2/5>2.7-2/5知识运用 练习21)2)3)<<≤定义五个特殊幂函数图象基本性质幂函数函数的奇偶性奇函数偶函数数学思想数形结合特殊到一般类比思想函数思想作业:1. P50练习题 ;
2. P51习题2-5A组1,3。
谢谢!
w 元(2)如果正方形的边长为 a,那么正方形的面积S = ____(3)如果立方体的边长为a,那么立方体的体积V = ____
(5)如果某人 t s内骑车行进1 km,那么他骑车的平均速度v=__________
____是____的函数a2 a3 V是a的函数t?1 km/s v是t 的函数(4)如果一个正方形场地的面积为 S,那么正方形的边长 a= _________a是S的函数以上问题中的函数具有什么共同特征?Pwy=xy=x2y=x3y=xy=x-1____是____的函数Sa知识回顾:一般的形如:y= xα (α R)的函数我们叫做幂函数,其中x是自变量,α是常数 幂函数定义域随指数α的不同而不同,未知数x是底数
(在中学阶段只关注α=1,2,3,1/2,-1这几种情形)指数为常数底数为自变量1探究新知:单项式练习1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
(5) y=x2 +2 (6) y=-x3我是例1 画出函数f(x)=x3的图像,讨论其单调性xyoy=x3--||11-1-1y=x3是R上的增函数大家还有什么发现?函数的图象关于原点对称对于任意x,都有f(-x)=-f(x)一般地,奇函数的图象关于原点对称,反过来,如果一个函数的图象关于原点对称,那么这个函数是奇函数。课堂典例讲练:对于函数y=x2呢?y=x2xy-1大家有什么类似发现?函数的图象关于y轴对称偶函数的图象关于y轴对称,反过来,如果一个函数的图象关于y轴对称,那么这个函数是偶函数 oy对于任意x,都有f(-x)=f(x)探究新知 (1)如果对于函数f(x)定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.
(2)如果对于函数f(x)定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数
如果函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性 函数的奇偶性判断方法:
法一:图像法
法二:定义法:(如下)步骤一:判断函数的定义域是否关于原点对称,如果对称进行步骤二,否则不具有奇偶性步骤二:归纳升华:例2 判断函数(1)f(x)= -2x5
(2)g(x)=x4+2
(3)h(x)=x4+2(x>0)的奇偶性 课堂典例讲练:加
油补全下面四个函数的图像动手实践下面研究幂函数在同一平面直角坐标系内作出这
六个幂函数的图象.
结合图象,研究性质:定义域、值域、单调性、奇偶性、过定点的情况等。研究 y=x知识提升:y=xxyoRR奇函数在R上
是增函数[0,+∞)在[0,+∞)上增,在[0,+∞)上增,R偶函数RR奇函数在R上
是增函数[0,+∞)[0,+∞)在[0,+∞)上增,非奇非
偶函数{x|x≠0}{y|y≠0}在(-∞,0)上减,在(0,+∞)上减奇函数奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当α>0时,图象随x增大而上升。
当α<0时,图象随x增大而下降
思维升华:图象都经过哪个定点?在第一象限内:
当a>0时,图象随x增大而上升,函数是增加的。
当a<0时,图象随x增大而下降,函数是减少的。图象都经过点(1,1)x=1a>0时,图象还都过点(0,0)点x=1右侧:图高指大幂函数在第四象限都没有图像练习: 如图所示,曲线是幂函数 y = xa在第一象限内的图象,已知 a分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1
的右侧,大指数在上,小指数在下,
在Y轴与直线x =1之间正好相反。 1C4C2C3C1
如果函数 是幂函数,且在区间(0,+∞)内是减少的,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1当 m=2时,函数为
当m=-1时,函数为因为m=-1不合题意,所以m=2即
m {m|m=2}知识巩固:
解:(1)y= x0.8在(0,+∞)内是增加的,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x-2/5在(0,+∞)内是减少的,
∵2.5<2.7∴ 2.5-2/5>2.7-2/5知识运用 练习21)2)3)<<≤定义五个特殊幂函数图象基本性质幂函数函数的奇偶性奇函数偶函数数学思想数形结合特殊到一般类比思想函数思想作业:1. P50练习题 ;
2. P51习题2-5A组1,3。
谢谢!
