一元二次方程根的分布 课件(24张PPT)
文档属性
| 名称 | 一元二次方程根的分布 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 716.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-07 15:27:11 | ||
图片预览




文档简介
课件24张PPT。 一元二次方程的实根分布问题
复习.函数零点一般地,对于函数y=f(x),我们把使f(x)=0的实数x就做函数y=f(x)的零点.
由此得出以下三个结论等价:
方程f(x)=0有实根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点 实根分布问题 ★一元二次方程1、当x为全体实数时的根
★一元二次方程 在某个区间
上有实根,求其中字母系数的问题称为实根分布问题。实根分布问题一般考虑四个方面,即:
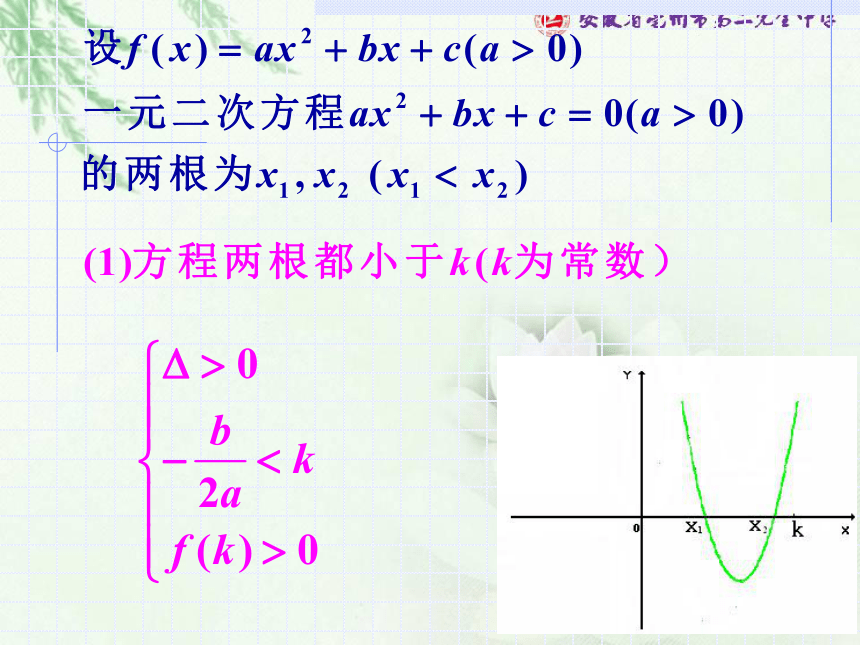
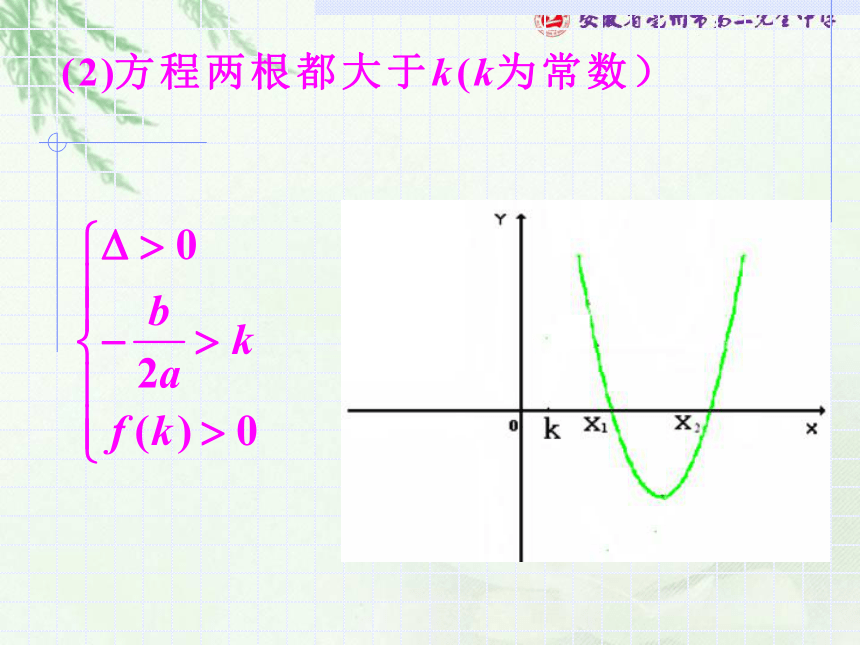
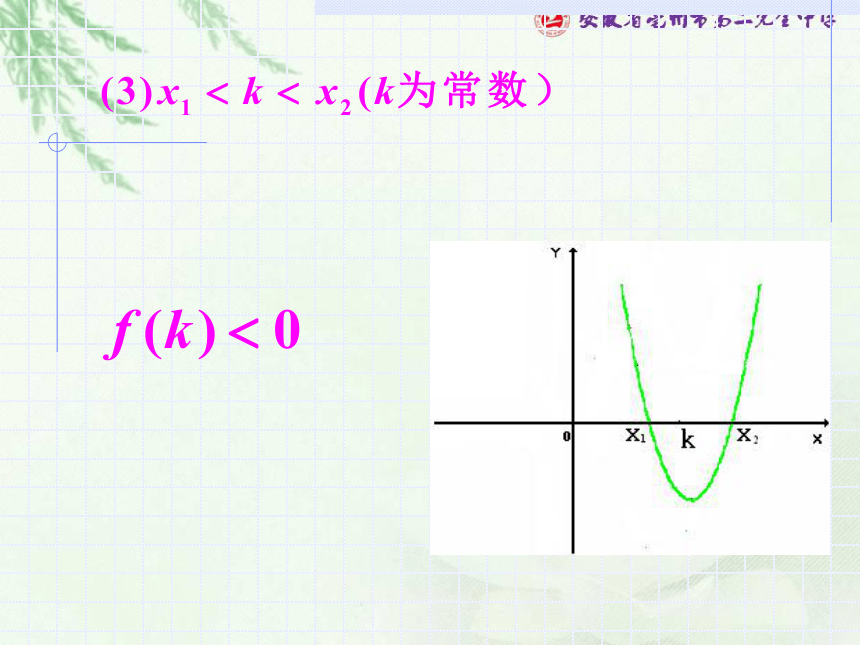
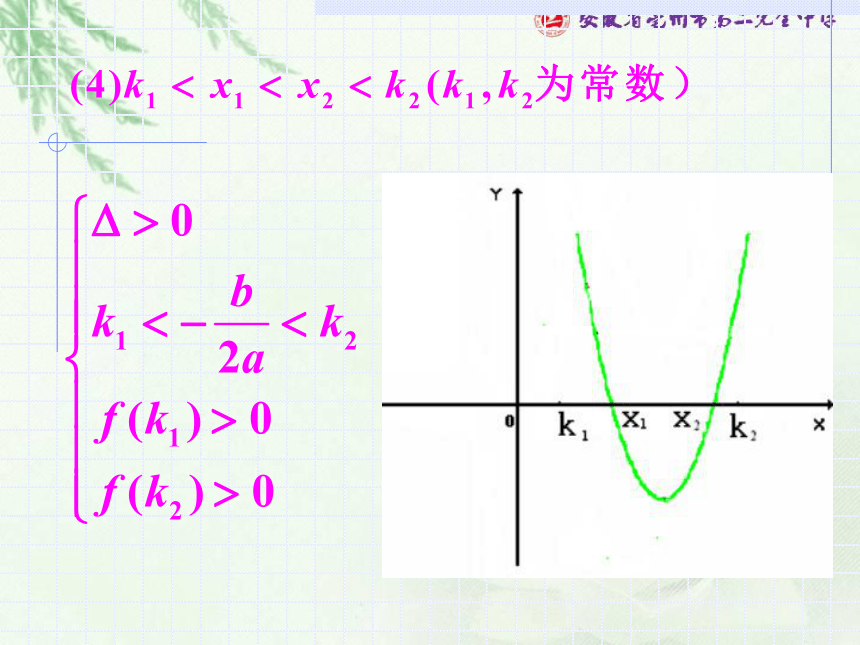
(1)开口方向
(2)判别式
(3)对称轴
(4)端点值 的符号。 2、当x在某个范围内的实根分布可用韦达定理表达式来书写条件也可可用韦达定理表达式来书写条件也可可用韦达定理表达式来书写:ac<0解: 寻求等价条件例1.m为何实数值时,关于x的方程
(1)有实根 (2)有两正根 (3)一正一负转变为函数,借助于图像,解不等式组法二:转化为韦达定理的
不等式组变式题:m为何实数值时,关于x的方程
有两个大于1的根.法三:由求根公式,转化成含根式的
不等式组解不等式组,得变式题:m为何实数值时,关于x的方程
有两个大于1的根.例3.就实数k的取值,讨论下列关于x的方程解的情况:结论:一元二次方程 在区间上的
实根分布问题. 注:前提 m,n不是方程(1)的根.课时小结: 紧紧以函数图像为中心,将方程的根用
图像直观的画出来,或数形结合或等价转
化,将函数、方程、不等式视为一个统一
整体,另外,要重视参数的分类讨论对图
形的影响。
复习.函数零点一般地,对于函数y=f(x),我们把使f(x)=0的实数x就做函数y=f(x)的零点.
由此得出以下三个结论等价:
方程f(x)=0有实根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点 实根分布问题 ★一元二次方程1、当x为全体实数时的根
★一元二次方程 在某个区间
上有实根,求其中字母系数的问题称为实根分布问题。实根分布问题一般考虑四个方面,即:
(1)开口方向
(2)判别式
(3)对称轴
(4)端点值 的符号。 2、当x在某个范围内的实根分布可用韦达定理表达式来书写条件也可可用韦达定理表达式来书写条件也可可用韦达定理表达式来书写:ac<0解: 寻求等价条件例1.m为何实数值时,关于x的方程
(1)有实根 (2)有两正根 (3)一正一负转变为函数,借助于图像,解不等式组法二:转化为韦达定理的
不等式组变式题:m为何实数值时,关于x的方程
有两个大于1的根.法三:由求根公式,转化成含根式的
不等式组解不等式组,得变式题:m为何实数值时,关于x的方程
有两个大于1的根.例3.就实数k的取值,讨论下列关于x的方程解的情况:结论:一元二次方程 在区间上的
实根分布问题. 注:前提 m,n不是方程(1)的根.课时小结: 紧紧以函数图像为中心,将方程的根用
图像直观的画出来,或数形结合或等价转
化,将函数、方程、不等式视为一个统一
整体,另外,要重视参数的分类讨论对图
形的影响。
