8数学广角 数与形 课件(26张PPT)
文档属性
| 名称 | 8数学广角 数与形 课件(26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-08 08:06:26 | ||
图片预览






文档简介
(共26张PPT)
数学是什么?
数学是什么?
数学是研究数量关系
和空间图形的
科学
一、激趣导入
游戏一:快速反应
10 =
8 =
7 =
3 =
( ) =81
( ) =25
( ) =16
( ) =1
64
100
9
9
5
4
49
1
游戏二:数
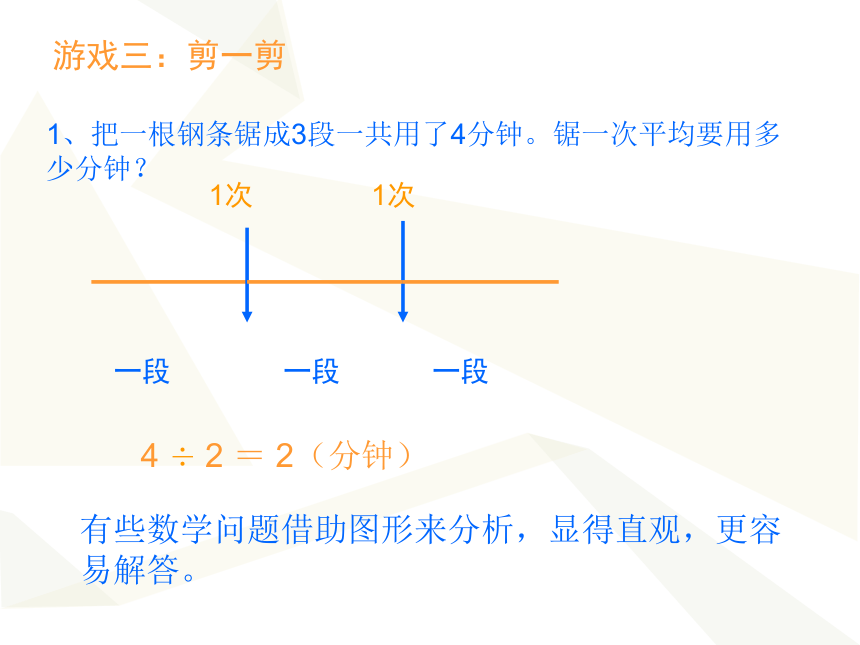
游戏三:剪一剪
1、把一根钢条锯成3段一共用了4分钟。锯一次平均要用多 少分钟?
一段
一段
一段
1次
1次
4 ÷ 2 = 2(分钟)
有些数学问题借助图形来分析,显得直观,更容易解答。
数无形时少直观,
形无数时难入微。
数形结合百般好,
割裂分家万事休。
----华罗庚
数与形
1
1+3
观察一下,下面三幅图中分别有多少个小正方形?用平方数表示分别是多少?
探究新知 例1
2
1
2
2
2
3
1+3+5
=
=
=
再观察,从左边图1到图2再到图3,依次增加了多少个小正方形?如果用加法算式怎么表示?
4=
9=
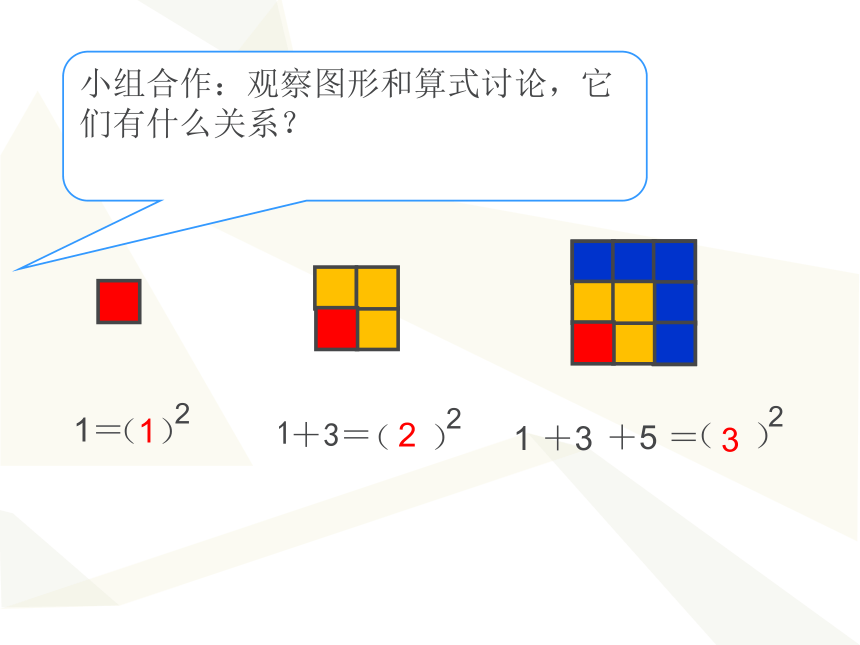
小组合作:观察图形和算式讨论,它们有什么关系?
1 +3
+5 =
( )
2
3
1
+3=
( )
2
2
( )
1
1=
2
从1开始,连续奇数相加的和就等于加数个数的平方。
9
52
11
62
13
72
1
3
5
7
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
1. 你能利用规律直接写一写吗?
4
7
如果遇到困难,可以画图来帮助。
1+3+5+7+9+11+13+15+17
=9
2
2
2
三、运用知识
1+3+5+7+5+3+1 =( )
2. 请根据例1的结论算一算。
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
运用知识
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
3. 请根据例1的结论算一算。
运用知识
1+3+5+7+5+3+1 =( 25)
6
2
7
2
3. 下面每个图中最外圈有多少个小正方形?
照这样画下去,第4个图形最外圈有( )个小正方形。
40
3 -1= 8
2
5 -3 = 16
2
2
7 -5 = 24
2
2
11 -9 = 40
2
2
运用知识
照这样画下去,第5个图形最外圈有( )个小正方形。
32
9 -7 = 32
2
2
每个图中最外圈各有多少个小正方形?你能解释这其中的道理吗?
16
8
24
32
40
8n
100以内数的认识
十 位
个 位
36是由 (3 )个十和(6) 个一组成的。
(
)
3
6
2
1
4
3
×
=
8
3
关于分数的学习:
75棵
杨树:
柳树:
比杨树多
5
4
?棵
柳树的棵树=杨树+柳树比杨树多的棵数
解决问题中画线段图表示数量关系
有着367种证明方式的勾股定理
a
b
c
毕达哥拉斯
古希腊
不需要语言的证明
三角形的两条斜边上都是数字1,而其余的数都等于它肩上的两个数字相加 。
杨辉三角
《详解九章算法》里记载过的表
杨辉
我国北宋数学家贾宪(约公元11世纪)已经用过“杨辉三角”,这表明我国发现这个表不晚于11世纪。在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角。杨辉三角的发现要比欧洲早500年左右。
中国古代数学史曾经有自己光辉灿烂的篇章,而杨辉三角的发现就是十分精彩的一页。这样一个三角在我们的数学学习中最简单的就是叫找规律。以后我们要学的二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。
今天你学到了什么?
数学是什么?
数学是什么?
数学是研究数量关系
和空间图形的
科学
一、激趣导入
游戏一:快速反应
10 =
8 =
7 =
3 =
( ) =81
( ) =25
( ) =16
( ) =1
64
100
9
9
5
4
49
1
游戏二:数
游戏三:剪一剪
1、把一根钢条锯成3段一共用了4分钟。锯一次平均要用多 少分钟?
一段
一段
一段
1次
1次
4 ÷ 2 = 2(分钟)
有些数学问题借助图形来分析,显得直观,更容易解答。
数无形时少直观,
形无数时难入微。
数形结合百般好,
割裂分家万事休。
----华罗庚
数与形
1
1+3
观察一下,下面三幅图中分别有多少个小正方形?用平方数表示分别是多少?
探究新知 例1
2
1
2
2
2
3
1+3+5
=
=
=
再观察,从左边图1到图2再到图3,依次增加了多少个小正方形?如果用加法算式怎么表示?
4=
9=
小组合作:观察图形和算式讨论,它们有什么关系?
1 +3
+5 =
( )
2
3
1
+3=
( )
2
2
( )
1
1=
2
从1开始,连续奇数相加的和就等于加数个数的平方。
9
52
11
62
13
72
1
3
5
7
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
1. 你能利用规律直接写一写吗?
4
7
如果遇到困难,可以画图来帮助。
1+3+5+7+9+11+13+15+17
=9
2
2
2
三、运用知识
1+3+5+7+5+3+1 =( )
2. 请根据例1的结论算一算。
25
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
运用知识
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
3. 请根据例1的结论算一算。
运用知识
1+3+5+7+5+3+1 =( 25)
6
2
7
2
3. 下面每个图中最外圈有多少个小正方形?
照这样画下去,第4个图形最外圈有( )个小正方形。
40
3 -1= 8
2
5 -3 = 16
2
2
7 -5 = 24
2
2
11 -9 = 40
2
2
运用知识
照这样画下去,第5个图形最外圈有( )个小正方形。
32
9 -7 = 32
2
2
每个图中最外圈各有多少个小正方形?你能解释这其中的道理吗?
16
8
24
32
40
8n
100以内数的认识
十 位
个 位
36是由 (3 )个十和(6) 个一组成的。
(
)
3
6
2
1
4
3
×
=
8
3
关于分数的学习:
75棵
杨树:
柳树:
比杨树多
5
4
?棵
柳树的棵树=杨树+柳树比杨树多的棵数
解决问题中画线段图表示数量关系
有着367种证明方式的勾股定理
a
b
c
毕达哥拉斯
古希腊
不需要语言的证明
三角形的两条斜边上都是数字1,而其余的数都等于它肩上的两个数字相加 。
杨辉三角
《详解九章算法》里记载过的表
杨辉
我国北宋数学家贾宪(约公元11世纪)已经用过“杨辉三角”,这表明我国发现这个表不晚于11世纪。在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角。杨辉三角的发现要比欧洲早500年左右。
中国古代数学史曾经有自己光辉灿烂的篇章,而杨辉三角的发现就是十分精彩的一页。这样一个三角在我们的数学学习中最简单的就是叫找规律。以后我们要学的二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。
今天你学到了什么?
