人教版高中数学必修二第一章空间几何体1.3空间几何体的表面积和体积(教师版)【优能辅导含答案】
文档属性
| 名称 | 人教版高中数学必修二第一章空间几何体1.3空间几何体的表面积和体积(教师版)【优能辅导含答案】 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 12:22:26 | ||
图片预览




文档简介
空间几何体的表面积和体积
__________________________________________________________________________________
__________________________________________________________________________________
能够熟练运用柱、锥、台、球的表面积和体积公式计算一些组合体的表面积和体积;
用联系、类比的方法解决一些有关空间几体的实际问题.
一、展开图定义
一些简单的多面体可以沿着多面体的某些棱将它剪开而成平面图形,这个平面图形叫做该多面体的平面展开图.
二、特殊几何体的定义
1.直棱柱:侧棱和底面垂直的棱柱叫做直棱柱.
2.正棱柱:底面为正多边形的直棱柱叫做正棱柱.
3.正棱锥:底面是正多边形,并且顶点在底面的正投影是底面的中心的棱锥叫正棱锥.
正棱锥的性质:
(1)正棱锥的侧棱相等;
(2)侧面是全等的等腰三角形;
(3)侧棱、高、底面构成直角三角形.
4.正棱台:正棱锥被平行于底面的平面所截,截面和底面之间的部分角正棱台.
正棱台的性质:
(1)正棱棱台的侧棱长相等
(2)侧面是全等的等腰三角形;
(3)高,侧棱,上、下底面的边心距构成直角梯形.
三、侧面积与表面积公式
1. 正棱柱、正棱锥、正棱台的侧面积与表面积公式
(1)设直棱柱高为h,底面多边形的周长为c,则直棱柱侧面积计算公式:S直棱柱侧=ch,即直棱柱的侧面积等于它的底面周长和高的乘积.
(2)设正n棱锥的底面边长为a,底面周长为c,斜高为h′,则正n棱锥的侧面积的计算公式:
S正棱锥侧= =.即正棱锥的侧面积等于它的底面周长和斜高乘积的一半.
(3)设正n棱台下底面边长为a、周长为c,上底面边长为a′、周长为c′,斜高为h′,则正n棱台的侧面积公式:S正棱台侧==.
(4)棱柱、棱锥、棱台的表面积(或全面积)等于底面积与侧面积的和,即S表=S底+S侧.
2. 圆柱、圆锥、圆台的侧面积与表面积公式
(1)S圆柱侧=(r为底面半径,l为母线长).
(2)S圆锥侧= (r为底面圆半径,l为母线长).
(3)S圆台侧= (R、r分别为上、下底面半径,l为母线长).
(4)圆柱、圆锥、圆台的表面积等于它的侧面积与底面积的和,即S表=S底+S侧.
(5) 若圆锥底面的半径为,侧面母线长为,侧面展开图扇形的圆心角为则,
3.由球的半径R计算球表面积的公式:S球=.即球面面积等于它的大圆面积的4倍.
四、体积
1.长方体的体积:
长方体的长、宽和高分别为a、b、c,长方体的体积V长方体=abc
2.棱柱和圆柱的体积:
(1)柱体(棱柱、圆柱)的体积等于它的底面积S和高h的积,即V柱体=Sh.
(2)底面半径是r,高是h的圆柱体的体积计算公式是V圆柱=.
3.棱锥和圆锥的体积:
(1)如果一个锥体(棱锥、圆锥)的底面积为S,高是h,那么它的体积V锥体=Sh.
(2)如果圆锥的底面半径是r,高是h,则它的体积是V圆锥=.
4.棱台和圆台的体积:
(1)如果台体的上、下底面面积分别为S′、S,高是h,则它的体积是V台体=.
(2)如果圆台的上、下底面半径分别是r′、r,高是h,则它的体积是V圆台=.
5.球的体积:
如果球的半径为R,那么球的体积V球=.
6.祖暅原理:幂势既同,则积不容异.
这就是说,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.应用祖暅原理可说明:等底面积、等高的两个柱体或锥体的体积相等.
7. 球面距离:在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度。我们把这个弧长叫做两点的球面距离.
类型一 表面积
例1: 已知正四棱台的上、下底面边长分别为3和6,其侧面积等于两底面面积之和,则该正四棱台的高是( )
A.2 B.
C.3 D.
解析:如图,设O1、O分别是正四棱台上、下底面的中心,则OO1是正棱台ABCD-A1B1C1D1的高,E1、E分别是A1D1、AD的中点,连接OE、O1E1,作E1H∥OO1,则E1H=O1O,由题意得,×4=9+36,∴EE1=.
在Rt△EHE1中,E1H2=EE-EH2=-=4,
∴E1H=2,∴O1O=2.
答案:A
练习1:某四棱锥的三视图如图所示,该四棱锥的表面积是( )
A.32 B.16+16
C.48 D.16+32
答案:B
练习2:若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的全面积是( )
A.3π B.3π
C.6π D.9π
答案:A
练习3:球的表面积与它的内接正方体的表面积之比是( )
A. B.
C. D.π
答案:C
例2: 用长为4,宽为2的矩形做侧面围成一个圆柱,此圆柱的轴截面面积为( )
A.8 B.
C. D.
解析:设围成圆柱的底面半径为r,则2πr=4,∴2r=,∴圆柱的轴截面面积为S=×2=.或2πr=2,∴2r=,
∴圆柱的轴截面面积为S=×4=.
答案:B
练习1: 某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90cm2
B.129cm2
C.132cm2
D.138cm2
答案:D
练习2:已知圆锥的表面积为12πcm2,且它的侧面展开图是一个半圆,则圆锥的底面半径为( )
A.cm B.2cm
C.2cm D.4cm
答案:B
练习3:某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90cm2
B.129cm2
C.132cm2
D.138cm2
答案:D
练习4:长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是________.
答案:50π
类型二 体积
例3:正三棱锥底面三角形的边长为,侧棱长为2,则其体积为( )
A. B.
C. D.
解析:如图,作PO⊥底面ABC,
∵正三角形ABC的边长为,
∴AO=×=1,
∴PO===,
∴VP-ABC=××()2×=.
答案:C
练习1:已知正四棱锥P-ABCD的底面边长为6,侧棱长为5,求四棱锥P-ABCD的体积和侧面积.
答案:连接AC、BD,AC与BD的交点为O,取BC的中点E,连接OE、PE、PO,则PO为正四棱锥P-ABCD的高,PE为斜高.
由已知得OE=3,OA=3,
∴PO===,
PE===4.
∴四棱锥P-ABCD的体积V=××6×6×
=6.
四棱锥P-ABCD的侧面积S=×6×4×4=48.
练习2:某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( )
A.3
B.2
C.
D.1
答案:D.由三视图可知,该几何体的体积V=Sh=××=1.由三视图找出垂直关系是关键.
例4:将长为a,宽为b(a>b)的长方形以a为轴旋转一周,所得柱体的体积为V1,以b为轴旋转一周,所得柱体的体积为V2,则有( )
A.V1>V2 B.V1C.V1=V2 D.V1与V2的大小关系不确定
解析:以a为旋转轴时,所得几何体的体积V1=ab2π,以b为旋转轴时,所得几何体的体积V2=a2bπ.
∴V1-V2=abπ(b-a),∵a>b,
∴V1-V2<0,∴V1答案:B
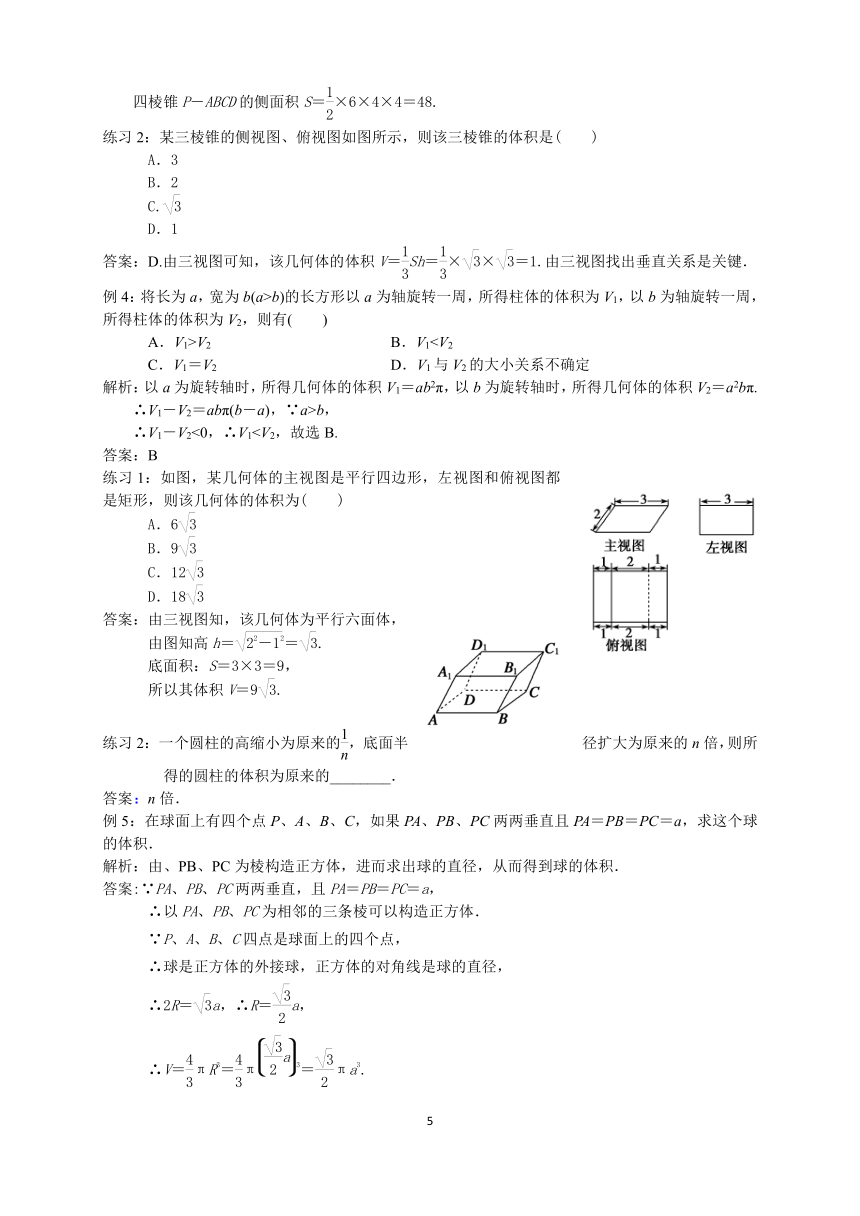
练习1:如图,某几何体的主视图是平行四边形,左视图和俯视图都是矩形,则该几何体的体积为( )
A.6
B.9
C.12
D.18
答案:由三视图知,该几何体为平行六面体,
由图知高h==.
底面积:S=3×3=9,
所以其体积V=9.
练习2:一个圆柱的高缩小为原来的,底面半径扩大为原来的n倍,则所得的圆柱的体积为原来的________.
答案:n倍.
例5:在球面上有四个点P、A、B、C,如果PA、PB、PC两两垂直且PA=PB=PC=a,求这个球的体积.
解析:由、PB、PC为棱构造正方体,进而求出球的直径,从而得到球的体积.
答案:∵PA、PB、PC两两垂直,且PA=PB=PC=a,
∴以PA、PB、PC为相邻的三条棱可以构造正方体.
∵P、A、B、C四点是球面上的四个点,
∴球是正方体的外接球,正方体的对角线是球的直径,
∴2R=a,∴R=a,
∴V=πR3=π3=πa3.
练习1:体积为8的一个正方体,其全面积与球O的表面积相等,则球O的体积等于________.
答案:设正方体棱长为a,球半径为r.
∵a3=8,∴a=2,又∵4πr2=6a2,∴r=.
∴V球=π3=.
练习2:平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
答案:B 本题考查球的截面性质,考查利用公式求球的体积.
设球O的半径为R,则R==,
故V球=πR3=4π.
1.将一个棱长为a的正方体,切成27个全等的小正方体,则表面积增加了( )
A.6a2 B.12a2
C.18a2 D.24a2
答案:B
2.正方体的八个顶点中有四个恰为正四面体的顶点,则正方体的全面积与正四面体的全面积之比为( )
A. B.
C. D.
答案:B
3.正四棱柱的体对角线长为6,侧面对角线长为3,则它的侧面积是________.
答案:36
4.若一棱锥的三视图如图所示,该三棱锥的体积为示)是边长为3、3、2的三角形,则该圆锥的侧面积为________.
答案: 3π
5.已知某几何体的俯视图是如图所示矩形.主视图是一个底边长为8、高为4的等腰三角形,左视图是一个底边长为6、高为4的等腰三角形.
(1)判断该几何体形状;
(2)求该几何体的侧面积S.
答案:(1) 这个几何体是四棱锥.
(2)作出该几何体的直观图,如图,E、F为AB、BC的中点,则AB=8,PO=4,BC=6.
在Rt△POF中,PF==4,
∴S△PBC=×6×4=12,在Rt△POE中,PE==5,∴S△PAB=×8×5=20,
所以侧面积为2(12+20)=24+40.
6. 若长方体的三个面的面积分别为,则长方体的体积为 ;其对角线长为 。
答案:,
7. 若圆锥的侧面展开图是半径为的半圆,则这个圆锥的体积是 。
答案:
8.正四棱台的斜高与上、下底面边长之比为,体积为,则棱台的高为 。
答案:
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1. 如果圆锥底面半径为,轴截面为等腰直角三角形,那么圆锥的全面积为( )
A、 B、 C、 D、
答案:B
2、一个圆台的母线长等于上、下底面半径和的一半,且侧面积是,则母线长为( )
A、 B、 C、 D、
答案:C
3、轴截面为正方形的圆柱的侧面积与全面积的比是( )
A、 B、 C、 D、
答案:B
4.某三棱锥的三视图如图所示,该三棱锥的体积为( )
A.2 B.3
C.4 D.6
答案:A
5. 已知圆锥的母线长为8,底面周长为6π,则它的体积是( )
A.9π B.9
C.3π D.3
答案:C
6.某几何体的三视图如图所示,则该几何体的体积为( )
A.12 B.18
C.24 D.30
答案:C
7.将半径为R的半圆卷成一个圆锥,这个圆锥的体积为____________.
答案:πR3
8.已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别为棱AA1与CC1的中点,求四棱锥A1-EBFD1的体积.
答案:如图所示,
VA1-EBFD1=VA1-EBF+VA1-EFD1=VF-A1EB+VF-A1ED1
=·a·+·a·=.
能力提升
9. 正过球面上三点A、B、C的截面到球心的距离是球半径R的一半,且AB=6,BC=8,AC=10,则球的表面积是( )
A.100π B.300π
C. D.π
答案:设球的半径为R,正方体的棱长为a,则=a3,∴a=R,S正方体=6a2=6×R2=R2,
S球=4πR2=R2=R2,
∴S球10. 一圆锥的底面半径为4,用平行于底面的截面截去底面半径为1的小圆锥后得到的圆台是原来圆锥的体积的( )
A. B.
C. D.
答案:轴截面如图,由题意==,
V圆锥PO1=·PO1,V圆锥PO=π·PO,
∴V圆台O1O=V圆锥PO-V圆锥PO1
=π·PO-·PO1=π·PO-··PO=π·PO,
∴==.
(或由:截得小圆锥底半径为1,原来底半径为4,∴相似比为1:4,故小圆锥与原来大圆锥体积比为1:64,∴截得圆台与原来大圆锥的体积比为63:64).
11.如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的全面积为( )
A. B.2π
C.π D.4π
答案:由几何体的三视图可知,该几何体是一个底面半径为,高为1的圆柱.
S圆柱侧=2πRh=2π××1=π.
S圆柱底=2πR2=,
∴圆柱的全面积为π+=.
12. 如图所示,在长方体ABCD-A′B′C′D′中,截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
答案:已知长方体可以看成直四棱柱ADD′A′-BCC′B′.
设它的底面ADD′A′的面积为S,高为h,
则棱锥C-A′DD′的底面积为S,高是h,
故棱锥C-A′DD′的体积为VC-A′DD′=×Sh=Sh.
余下的体积是Sh-Sh=Sh.
所以棱锥C-A′DD′的体积与剩余部分的体积之比为1:5.
13.如图所示,在边长为5+2的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M、N、K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
答案:设圆锥的母线长为l,底面半径为r,高为h,由已知得,
解得r=,l=4,
h==,
∴S=πrl+πr2=10π,V=πr2h=π.
10
__________________________________________________________________________________
__________________________________________________________________________________
能够熟练运用柱、锥、台、球的表面积和体积公式计算一些组合体的表面积和体积;
用联系、类比的方法解决一些有关空间几体的实际问题.
一、展开图定义
一些简单的多面体可以沿着多面体的某些棱将它剪开而成平面图形,这个平面图形叫做该多面体的平面展开图.
二、特殊几何体的定义
1.直棱柱:侧棱和底面垂直的棱柱叫做直棱柱.
2.正棱柱:底面为正多边形的直棱柱叫做正棱柱.
3.正棱锥:底面是正多边形,并且顶点在底面的正投影是底面的中心的棱锥叫正棱锥.
正棱锥的性质:
(1)正棱锥的侧棱相等;
(2)侧面是全等的等腰三角形;
(3)侧棱、高、底面构成直角三角形.
4.正棱台:正棱锥被平行于底面的平面所截,截面和底面之间的部分角正棱台.
正棱台的性质:
(1)正棱棱台的侧棱长相等
(2)侧面是全等的等腰三角形;
(3)高,侧棱,上、下底面的边心距构成直角梯形.
三、侧面积与表面积公式
1. 正棱柱、正棱锥、正棱台的侧面积与表面积公式
(1)设直棱柱高为h,底面多边形的周长为c,则直棱柱侧面积计算公式:S直棱柱侧=ch,即直棱柱的侧面积等于它的底面周长和高的乘积.
(2)设正n棱锥的底面边长为a,底面周长为c,斜高为h′,则正n棱锥的侧面积的计算公式:
S正棱锥侧= =.即正棱锥的侧面积等于它的底面周长和斜高乘积的一半.
(3)设正n棱台下底面边长为a、周长为c,上底面边长为a′、周长为c′,斜高为h′,则正n棱台的侧面积公式:S正棱台侧==.
(4)棱柱、棱锥、棱台的表面积(或全面积)等于底面积与侧面积的和,即S表=S底+S侧.
2. 圆柱、圆锥、圆台的侧面积与表面积公式
(1)S圆柱侧=(r为底面半径,l为母线长).
(2)S圆锥侧= (r为底面圆半径,l为母线长).
(3)S圆台侧= (R、r分别为上、下底面半径,l为母线长).
(4)圆柱、圆锥、圆台的表面积等于它的侧面积与底面积的和,即S表=S底+S侧.
(5) 若圆锥底面的半径为,侧面母线长为,侧面展开图扇形的圆心角为则,
3.由球的半径R计算球表面积的公式:S球=.即球面面积等于它的大圆面积的4倍.
四、体积
1.长方体的体积:
长方体的长、宽和高分别为a、b、c,长方体的体积V长方体=abc
2.棱柱和圆柱的体积:
(1)柱体(棱柱、圆柱)的体积等于它的底面积S和高h的积,即V柱体=Sh.
(2)底面半径是r,高是h的圆柱体的体积计算公式是V圆柱=.
3.棱锥和圆锥的体积:
(1)如果一个锥体(棱锥、圆锥)的底面积为S,高是h,那么它的体积V锥体=Sh.
(2)如果圆锥的底面半径是r,高是h,则它的体积是V圆锥=.
4.棱台和圆台的体积:
(1)如果台体的上、下底面面积分别为S′、S,高是h,则它的体积是V台体=.
(2)如果圆台的上、下底面半径分别是r′、r,高是h,则它的体积是V圆台=.
5.球的体积:
如果球的半径为R,那么球的体积V球=.
6.祖暅原理:幂势既同,则积不容异.
这就是说,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.应用祖暅原理可说明:等底面积、等高的两个柱体或锥体的体积相等.
7. 球面距离:在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度。我们把这个弧长叫做两点的球面距离.
类型一 表面积
例1: 已知正四棱台的上、下底面边长分别为3和6,其侧面积等于两底面面积之和,则该正四棱台的高是( )
A.2 B.
C.3 D.
解析:如图,设O1、O分别是正四棱台上、下底面的中心,则OO1是正棱台ABCD-A1B1C1D1的高,E1、E分别是A1D1、AD的中点,连接OE、O1E1,作E1H∥OO1,则E1H=O1O,由题意得,×4=9+36,∴EE1=.
在Rt△EHE1中,E1H2=EE-EH2=-=4,
∴E1H=2,∴O1O=2.
答案:A
练习1:某四棱锥的三视图如图所示,该四棱锥的表面积是( )
A.32 B.16+16
C.48 D.16+32
答案:B
练习2:若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的全面积是( )
A.3π B.3π
C.6π D.9π
答案:A
练习3:球的表面积与它的内接正方体的表面积之比是( )
A. B.
C. D.π
答案:C
例2: 用长为4,宽为2的矩形做侧面围成一个圆柱,此圆柱的轴截面面积为( )
A.8 B.
C. D.
解析:设围成圆柱的底面半径为r,则2πr=4,∴2r=,∴圆柱的轴截面面积为S=×2=.或2πr=2,∴2r=,
∴圆柱的轴截面面积为S=×4=.
答案:B
练习1: 某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90cm2
B.129cm2
C.132cm2
D.138cm2
答案:D
练习2:已知圆锥的表面积为12πcm2,且它的侧面展开图是一个半圆,则圆锥的底面半径为( )
A.cm B.2cm
C.2cm D.4cm
答案:B
练习3:某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90cm2
B.129cm2
C.132cm2
D.138cm2
答案:D
练习4:长方体的一个顶点上三条棱长分别是3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是________.
答案:50π
类型二 体积
例3:正三棱锥底面三角形的边长为,侧棱长为2,则其体积为( )
A. B.
C. D.
解析:如图,作PO⊥底面ABC,
∵正三角形ABC的边长为,
∴AO=×=1,
∴PO===,
∴VP-ABC=××()2×=.
答案:C
练习1:已知正四棱锥P-ABCD的底面边长为6,侧棱长为5,求四棱锥P-ABCD的体积和侧面积.
答案:连接AC、BD,AC与BD的交点为O,取BC的中点E,连接OE、PE、PO,则PO为正四棱锥P-ABCD的高,PE为斜高.
由已知得OE=3,OA=3,
∴PO===,
PE===4.
∴四棱锥P-ABCD的体积V=××6×6×
=6.
四棱锥P-ABCD的侧面积S=×6×4×4=48.
练习2:某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( )
A.3
B.2
C.
D.1
答案:D.由三视图可知,该几何体的体积V=Sh=××=1.由三视图找出垂直关系是关键.
例4:将长为a,宽为b(a>b)的长方形以a为轴旋转一周,所得柱体的体积为V1,以b为轴旋转一周,所得柱体的体积为V2,则有( )
A.V1>V2 B.V1
解析:以a为旋转轴时,所得几何体的体积V1=ab2π,以b为旋转轴时,所得几何体的体积V2=a2bπ.
∴V1-V2=abπ(b-a),∵a>b,
∴V1-V2<0,∴V1
练习1:如图,某几何体的主视图是平行四边形,左视图和俯视图都是矩形,则该几何体的体积为( )
A.6
B.9
C.12
D.18
答案:由三视图知,该几何体为平行六面体,
由图知高h==.
底面积:S=3×3=9,
所以其体积V=9.
练习2:一个圆柱的高缩小为原来的,底面半径扩大为原来的n倍,则所得的圆柱的体积为原来的________.
答案:n倍.
例5:在球面上有四个点P、A、B、C,如果PA、PB、PC两两垂直且PA=PB=PC=a,求这个球的体积.
解析:由、PB、PC为棱构造正方体,进而求出球的直径,从而得到球的体积.
答案:∵PA、PB、PC两两垂直,且PA=PB=PC=a,
∴以PA、PB、PC为相邻的三条棱可以构造正方体.
∵P、A、B、C四点是球面上的四个点,
∴球是正方体的外接球,正方体的对角线是球的直径,
∴2R=a,∴R=a,
∴V=πR3=π3=πa3.
练习1:体积为8的一个正方体,其全面积与球O的表面积相等,则球O的体积等于________.
答案:设正方体棱长为a,球半径为r.
∵a3=8,∴a=2,又∵4πr2=6a2,∴r=.
∴V球=π3=.
练习2:平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
答案:B 本题考查球的截面性质,考查利用公式求球的体积.
设球O的半径为R,则R==,
故V球=πR3=4π.
1.将一个棱长为a的正方体,切成27个全等的小正方体,则表面积增加了( )
A.6a2 B.12a2
C.18a2 D.24a2
答案:B
2.正方体的八个顶点中有四个恰为正四面体的顶点,则正方体的全面积与正四面体的全面积之比为( )
A. B.
C. D.
答案:B
3.正四棱柱的体对角线长为6,侧面对角线长为3,则它的侧面积是________.
答案:36
4.若一棱锥的三视图如图所示,该三棱锥的体积为示)是边长为3、3、2的三角形,则该圆锥的侧面积为________.
答案: 3π
5.已知某几何体的俯视图是如图所示矩形.主视图是一个底边长为8、高为4的等腰三角形,左视图是一个底边长为6、高为4的等腰三角形.
(1)判断该几何体形状;
(2)求该几何体的侧面积S.
答案:(1) 这个几何体是四棱锥.
(2)作出该几何体的直观图,如图,E、F为AB、BC的中点,则AB=8,PO=4,BC=6.
在Rt△POF中,PF==4,
∴S△PBC=×6×4=12,在Rt△POE中,PE==5,∴S△PAB=×8×5=20,
所以侧面积为2(12+20)=24+40.
6. 若长方体的三个面的面积分别为,则长方体的体积为 ;其对角线长为 。
答案:,
7. 若圆锥的侧面展开图是半径为的半圆,则这个圆锥的体积是 。
答案:
8.正四棱台的斜高与上、下底面边长之比为,体积为,则棱台的高为 。
答案:
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1. 如果圆锥底面半径为,轴截面为等腰直角三角形,那么圆锥的全面积为( )
A、 B、 C、 D、
答案:B
2、一个圆台的母线长等于上、下底面半径和的一半,且侧面积是,则母线长为( )
A、 B、 C、 D、
答案:C
3、轴截面为正方形的圆柱的侧面积与全面积的比是( )
A、 B、 C、 D、
答案:B
4.某三棱锥的三视图如图所示,该三棱锥的体积为( )
A.2 B.3
C.4 D.6
答案:A
5. 已知圆锥的母线长为8,底面周长为6π,则它的体积是( )
A.9π B.9
C.3π D.3
答案:C
6.某几何体的三视图如图所示,则该几何体的体积为( )
A.12 B.18
C.24 D.30
答案:C
7.将半径为R的半圆卷成一个圆锥,这个圆锥的体积为____________.
答案:πR3
8.已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别为棱AA1与CC1的中点,求四棱锥A1-EBFD1的体积.
答案:如图所示,
VA1-EBFD1=VA1-EBF+VA1-EFD1=VF-A1EB+VF-A1ED1
=·a·+·a·=.
能力提升
9. 正过球面上三点A、B、C的截面到球心的距离是球半径R的一半,且AB=6,BC=8,AC=10,则球的表面积是( )
A.100π B.300π
C. D.π
答案:设球的半径为R,正方体的棱长为a,则=a3,∴a=R,S正方体=6a2=6×R2=R2,
S球=4πR2=R2=R2,
∴S球
A. B.
C. D.
答案:轴截面如图,由题意==,
V圆锥PO1=·PO1,V圆锥PO=π·PO,
∴V圆台O1O=V圆锥PO-V圆锥PO1
=π·PO-·PO1=π·PO-··PO=π·PO,
∴==.
(或由:截得小圆锥底半径为1,原来底半径为4,∴相似比为1:4,故小圆锥与原来大圆锥体积比为1:64,∴截得圆台与原来大圆锥的体积比为63:64).
11.如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的全面积为( )
A. B.2π
C.π D.4π
答案:由几何体的三视图可知,该几何体是一个底面半径为,高为1的圆柱.
S圆柱侧=2πRh=2π××1=π.
S圆柱底=2πR2=,
∴圆柱的全面积为π+=.
12. 如图所示,在长方体ABCD-A′B′C′D′中,截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
答案:已知长方体可以看成直四棱柱ADD′A′-BCC′B′.
设它的底面ADD′A′的面积为S,高为h,
则棱锥C-A′DD′的底面积为S,高是h,
故棱锥C-A′DD′的体积为VC-A′DD′=×Sh=Sh.
余下的体积是Sh-Sh=Sh.
所以棱锥C-A′DD′的体积与剩余部分的体积之比为1:5.
13.如图所示,在边长为5+2的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M、N、K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
答案:设圆锥的母线长为l,底面半径为r,高为h,由已知得,
解得r=,l=4,
h==,
∴S=πrl+πr2=10π,V=πr2h=π.
10
