人教版高中数学必修二第二章点直线平面之间的位置关系2.2直线、平面平行的判定及其性质(教师版)【优能辅导含答案】
文档属性
| 名称 | 人教版高中数学必修二第二章点直线平面之间的位置关系2.2直线、平面平行的判定及其性质(教师版)【优能辅导含答案】 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 12:22:57 | ||
图片预览



文档简介
直线、平面平行的判定及其性质
__________________________________________________________________________________
__________________________________________________________________________________
了解直线和平面的三种位置关系;
理解并掌握直线与平面平行的判定定理;
理解并掌握直线与平面平行的性质定理;
理解并掌握平面与平面平行的性质定理.
一、直线与平面的位置关系
位置关系 交点个数 图形语言 符号语言
直线在平面内 无数个
直线在平面外 直线与平面相交 只有一个
直线与平面平行 没有
直线和平面平行
1.定义:如果一条直线和一个平面没有公共点,那么这条直线与这个平面平行.
2.判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
推理模式:
特别说明:
1、定理中的三个条件缺一不可.
2、该定理的作用:证明线面平行.
3、该定理可简记为“线线平行,则线面平行.”
3. 性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.
推理模式
特别说明:
1、定理中的三个条件缺一不可. 2、该定理的作用:证明线线平行.
3、该定理可简记为“线面平行,则线线平行.”
三、平面和平面的位置关系
位置关系 两平面平行 两平面相交
公共点 没有公共点 有一条公共直线
符号表示
图形表示
四、平面与平面平行
1.两平面互相平行的定义
如果两个平面没有公共点,那么这两个平面平行.
2.两平面平行的判定定理
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
推理模式:.简言之:线面平行面面平行
推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行.
3.两个平面平行的性质
如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
推理模式:.简言之:面面平行线线平行
特别说明:
平面与平面平行的其它性质
(1)两个平面平行,其中一个平面内的任何一条直线必平行于另一个平面.
(2)夹在两个平行平面之间的平行线段相等.
(3)经过平面外一点,有且仅有一个平面和已知平面平行.
(4)两条直线被三个平行平面所截,截得的对应线段成比例.
类型一 线面平行
例1:b是平面α外的一条直线,可以推出b∥α的条件是( )
A.b与α内的一条直线不相交
B.b与α内的两条直线不相交
C.b与α内的无数条直线不相交
D.b与α内的任何一条直线都不相交
解析: ∵b∥α,∴b与α无公共点,从而b与α内任何一条直线无公共点.
答案:D
练习1: 直线在平面外是指( )
A.直线与平面没有公共点
B.直线与平面相交
C.直线与平面平行
D.直线与平面最多有一个公共点
答案:D
练习2:点M、N是正方体ABCD-A1B1C1D1的棱A1A与A1B1的中点,P是正方形ABCD的中心,则MN与平面PCB1的位置关系是( )
A.平行
B.相交
C.MN?平面PCB1
D.以上三种情形都有可能
答案:A
如图,∵M、N分别为A1A和A1B1中点,
∴MN∥AB1,
又∵P是正方形ABCD的中心,∴P、A、C三点共线,
∴AB1?平面PB1C,
∵MN?平面PB1C,∴MN∥平面PB1C.
练习3:在正方体ABCD-A1B1C1D1中和平面C1DB平行的侧面对角线有________条.
答案:3
例2: 如图,已知E、F分别是三棱锥A-BCD的侧棱AB、AD的中点,求证:EF∥平面BCD.
解析:找到平面BCD中与EF平行的直线,即可由定理证明结论.
答案:证明:∵E、F分别是AB、AD的中点,∴EF∥BD.
又∵EF?平面BCD,BD?平面BCD,
∴EF∥平面BCD.
练习1: 如图所示,已知P是?ABCD所在平面外的一点,M是PB的中点,求证:PD∥平面MAC.
答案:连接BD交AC于点O,连接OM.
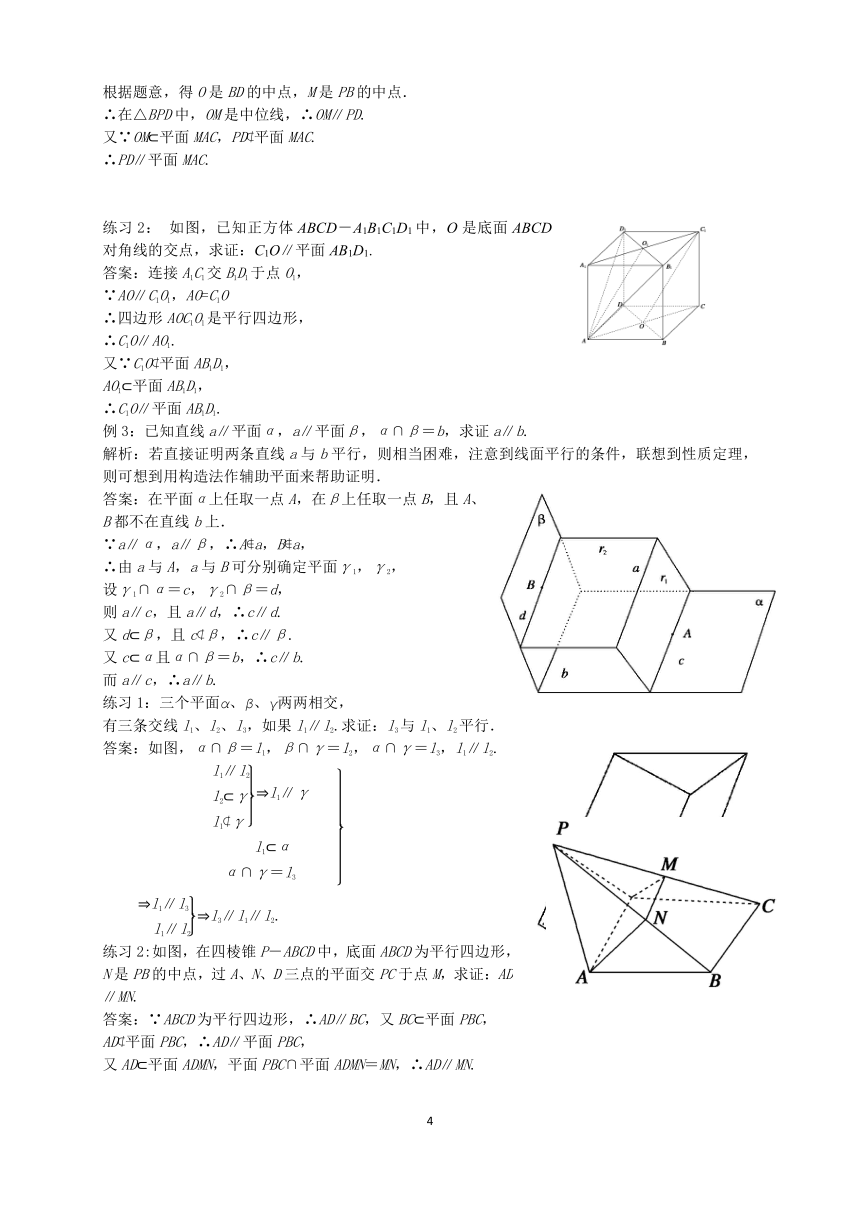
根据题意,得O是BD的中点,M是PB的中点.
∴在△BPD中,OM是中位线,∴OM∥PD.
又∵OM?平面MAC,PD?平面MAC.
∴PD∥平面MAC.
练习2: 如图,已知正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点,求证:C1O∥平面AB1D1.
答案:连接A1C1交B1D1于点O1,
∵AO∥C1O1,AO=C1O
∴四边形AOC1O1是平行四边形,
∴C1O∥AO1.
又∵C1O?平面AB1D1,
AO1?平面AB1D1,
∴C1O∥平面AB1D1.
例3:已知直线a∥平面α,a∥平面β,α∩β=b,求证a∥b.
解析:若直接证明两条直线a与b平行,则相当困难,注意到线面平行的条件,联想到性质定理,则可想到用构造法作辅助平面来帮助证明.
答案:在平面α上任取一点A,在β上任取一点B,且A、B都不在直线b上.
∵a∥α,a∥β,∴A?a,B?a,
∴由a与A,a与B可分别确定平面γ1,γ2,
设γ1∩α=c,γ2∩β=d,
则a∥c,且a∥d,∴c∥d.
又d?β,且c?β,∴c∥β.
又c?α且α∩β=b,∴c∥b.
而a∥c,∴a∥b.
练习1:三个平面α、β、γ两两相交,
有三条交线l1、l2、l3,如果l1∥l2.求证:l3与l1、l2平行.
答案:如图,α∩β=l1,β∩γ=l2,α∩γ=l3,l1∥l2.
练习2:如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB的中点,过A、N、D三点的平面交PC于点M,求证:AD ∥MN.
答案:∵ABCD为平行四边形,∴AD∥BC,又BC?平面PBC,
AD?平面PBC,∴AD∥平面PBC,
又AD?平面ADMN,平面PBC∩平面ADMN=MN,∴AD∥MN.
类型二 平面与平面平行
例3:如图,在三棱柱ABC-A1B1C1中,E、F、G、H分别是AB、AC、A1B1、A1C1的中点,求证:平面EFA1∥平面BCHG.
解析:运用平面平行的判定.
答案: ∵E、F分别为AB、AC的中点,
∴EF∥BC.
∵EF?平面BCHG,BC?平面BCHG,
∴EF∥平面BCHG.
∵A1GEB,
∴四边形A1EBG是平行四边形,
∴A1E∥GB.
∵A1E?平面BCHG,GB?平面BCHG,
∴A1E∥平面BCHG.
∵A1E∩EF=E,∴平面EFA1∥平面BCHG.
练习1:如图所示,已知正方体ABCD-A1B1C1D1,
求证:平面AB1D1∥平面BDC1.
答案: ∵ABA1B1,C1D1A1B1,∴ABC1D1.
∴四边形ABC1D1为平行四边形.
∴AD1∥BC1.
又AD1?平面AB1D1,BC1?平面AB1D1,
∴BC1∥平面AB1D1.
同理BD∥平面AB1D1.
又∵BD∩BC1=B,∴平面AB1D1∥平面BDC1.
练习2:已知正方体ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,求证:平面BDF∥平面B1D1E.
答案:如图,取BB1的中点G,连接EG、GC1,
则有EGA1B1.
又A1B1C1D1,∴EGC1D1.
∴四边形EGC1D1是平行四边形,
∴D1EGC1.又BGC1F,
∴四边形BGC1F为平行四边形,
∴BF∥C1G,∴BF∥D1E.
又BF?平面B1D1E,D1E?平面B1D1E,
∴BF∥平面B1D1E.
又BD∥B1D1,
同理可得BD∥平面B1D1E.
又∵BF∩BD=B,
∴由平面与平面平行的判定定理得,
平面BDF∥平面B1D1E.
练习3:在正方体EFGH-E1F1G1H1中,平面E1FG1与平面EGH1,平面FHG1与平面F1H1G,平面F1H1H与平面FHE1,平面E1HG1与平面EH1G中互相平行的对数为( )
A.0 B.1
C.2 D.3
答案:本题考查面面平行的判定.∵EG∥E1G1,FG1∥EH1,EG∩EH1=E,E1G1∩FG1=G1,
∴平面EGH1∥平面E1FG1,经验证其他3对均不平行,故选B.
例4:将已知:平面α∥平面β,AB、CD是夹在这两个平面之间的线段,
且点E、G分别为AB、CD的中点,AB不平行于CD,如图所示.
求证:EG∥α,EG∥β.
解析:由平面平行的性质除法得到结论.
答案:如图所示,过点A作AH∥CD,交平面β于点H,
设F是AH的中点,连接HD,则AH綊CD,
∴四边形ACDH为平行四边形.
连接EF、FG和BH,
∵E、F分别是AB、AH的中点,∴EF∥BH.
∵EF?平面β,且BH?平面β,∴EF∥β.
又F、G分别是AH,CD的中点,且AC∥HD,
∴FG∥HD.又∵FG?平面β,HD?平面β,∴FG∥β.
∵EF∩FG=F,∴平面EFG∥β,
又α∥β,∴平面EFG∥α.
∵EG?平面EFC,∴EG∥α,EG∥β.
练习1:知平面α、β、γ,α∥β∥γ,
异面直线l、m分别与平面α、β、γ相交于A、B、C和D、E、F.
求证:=.
答案:连接DC,设DC与平面β相交于G,
则平面ACD与平面α、β分别交于AD、BG,
平面DCF与平面β、γ分别相交于直线GE、CF,
∵α∥β,β∥γ,∴BG∥AD,GE∥CF,
∴=,=,∴=.
练习2:若平面α∥平面β,直线a?α,直线b?β,那么a、b的位置关系是( )
A.无公共点 B.平行
C.既不平行也不相交 D.相交
答案:A
1. 已知直线a、b和平面α,下列命题中正确的是( )
A.若a∥α,b?α,则a∥b
B.若a∥α,b∥α,则a∥b
C.若a∥b,b?α,则a∥α
D.若a∥b,a∥α,则b?α或b∥α
答案:D
2.P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出四个命题:
①OM∥平面PCD;②OM∥平面PBC;③OM∥平面PDA;④OM∥平面PBA.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
答案:B
3.过平面α外的直线l,作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为( )
A.都平行
B.都相交且交于同一点
C.都相交但不一定交于同一点
D.都平行或都交于同一点
答案:D
4.如图,在空间四边形ABCD中,M∈AB,N∈AD,若=,则MN与平面BDC的位置关系是________.
答案: 平行
5.在下列条件中,可判断平面与平面平行的是( )
A、都垂直于 B、内存在不共线的三点到的距离相等
C、是内两条直线,且 D、是两条异面直线,且
答案:D
6. 有下列几个命题:
①平面α内有无数个点到平面β的距离相等,则α∥β;
②α∩γ=a,α∩β=b,且a∥b(α、β、γ分别表示平面,a、b表示直线),则γ∥β;
③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边,则α∥β;
④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行,则α∥β.
其中正确的有________.(填序号)
答案: ③
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1. 已知直线a、b和平面α,下列命题中正确的是( )
A.若a∥α,b?α,则a∥b
B.若a∥α,b∥α,则a∥b
C.若a∥b,b?α,则a∥α
D.若a∥b,a∥α,则b?α或b∥α
答案: D若a∥α,b?α,则a∥b或a与b是异面直线;若a∥α,b∥α,则a与b相交、平行或异面;若a∥b,b?α,则a∥α或a?α,故选D.
2.P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出四个命题:
①OM∥平面PCD;②OM∥平面PBC;③OM∥平面PDA;④OM∥平面PBA.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
答案: B 由已知OM∥PD,∴OM∥平面PCD且OM∥平面PAD.故正确的只有①③,选B.
3.过平面α外的直线l,作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为( )
A.都平行
B.都相交且交于同一点
C.都相交但不一定交于同一点
D.都平行或都交于同一点
答案: D
4..若平面α∥平面β,直线a?α,直线b?β,那么a、b的位置关系是( )
A.无公共点 B.平行
C.既不平行也不相交 D.相交
答案:A
5.若两直线a、b相交,且a∥平面α,则b与α的位置关系是________.
答案:相交或平行
能力提升
6.若平面α∥β,直线a?α,点B∈β,则在β内过点B的所有直线中( )
A.不一定存在与a平行的直线
B.只有两条直线与a平行
C.存在无数条直线与a平行
D.存在惟一一条与a平行的直线
答案:D
7. 已知a是一条直线,过a作平面β,使β∥平面α,这样的β( )
A.只能作一个 B.至少有一个
C.不存在 D.至多有一个
答案:D
8. 已知α∥β,O是两平面外一点,过O作三条直线和平面α交于不在同一直线上的A、B、C三点,和平面β交于A′、B′、C′三点,则△ABC与△A′B′C′的关系是________,若AB=a,A′B′=b,B′C′=c,则BC的长是________.
答案:相似
9. 在正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________________时,有MN∥平面B1BDD1.
答案:M在线段FH上移动
10. 正方体ABCD-A1B1C1D1中,平面AA1C1C和平面BB1D1D的交线与棱CC1的位置关系是________,截面BA1C1和直线AC的位置关系是________.
答案:平行 平行
11. 在正方体ABCD-A1B1C1D1,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点,如图所示.
(1)求证:E、F、B、D四点共面;
(2)求证:平面AMN∥平面EFBD.
答案:(1)分别连接BD、ED、FB,由正方体性质知,B1D1∥BD.
∵E、F分别是C1D1和B1C1的中点,
∴EFB1D1,EFBD.
∴E、F、B、D四点共面.
(2)连接A1C1交MN于P点,交EF于点Q,分别连接PA、QO.∵M、N分别为A1B1、A1D1的中点,
∴MN∥EF,EF?面EFBD,∴MN∥面EFBD.
∵PQAO,∴四边形PAOQ为平行四边形,
∴PA∥QO.而QO?面EFBD,
∵PA∥面EFBD,且PA∩MN=P,PA、MN?面AMN,
∴平面AMN∥面EFBD.
1
__________________________________________________________________________________
__________________________________________________________________________________
了解直线和平面的三种位置关系;
理解并掌握直线与平面平行的判定定理;
理解并掌握直线与平面平行的性质定理;
理解并掌握平面与平面平行的性质定理.
一、直线与平面的位置关系
位置关系 交点个数 图形语言 符号语言
直线在平面内 无数个
直线在平面外 直线与平面相交 只有一个
直线与平面平行 没有
直线和平面平行
1.定义:如果一条直线和一个平面没有公共点,那么这条直线与这个平面平行.
2.判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
推理模式:
特别说明:
1、定理中的三个条件缺一不可.
2、该定理的作用:证明线面平行.
3、该定理可简记为“线线平行,则线面平行.”
3. 性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.
推理模式
特别说明:
1、定理中的三个条件缺一不可. 2、该定理的作用:证明线线平行.
3、该定理可简记为“线面平行,则线线平行.”
三、平面和平面的位置关系
位置关系 两平面平行 两平面相交
公共点 没有公共点 有一条公共直线
符号表示
图形表示
四、平面与平面平行
1.两平面互相平行的定义
如果两个平面没有公共点,那么这两个平面平行.
2.两平面平行的判定定理
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
推理模式:.简言之:线面平行面面平行
推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行.
3.两个平面平行的性质
如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
推理模式:.简言之:面面平行线线平行
特别说明:
平面与平面平行的其它性质
(1)两个平面平行,其中一个平面内的任何一条直线必平行于另一个平面.
(2)夹在两个平行平面之间的平行线段相等.
(3)经过平面外一点,有且仅有一个平面和已知平面平行.
(4)两条直线被三个平行平面所截,截得的对应线段成比例.
类型一 线面平行
例1:b是平面α外的一条直线,可以推出b∥α的条件是( )
A.b与α内的一条直线不相交
B.b与α内的两条直线不相交
C.b与α内的无数条直线不相交
D.b与α内的任何一条直线都不相交
解析: ∵b∥α,∴b与α无公共点,从而b与α内任何一条直线无公共点.
答案:D
练习1: 直线在平面外是指( )
A.直线与平面没有公共点
B.直线与平面相交
C.直线与平面平行
D.直线与平面最多有一个公共点
答案:D
练习2:点M、N是正方体ABCD-A1B1C1D1的棱A1A与A1B1的中点,P是正方形ABCD的中心,则MN与平面PCB1的位置关系是( )
A.平行
B.相交
C.MN?平面PCB1
D.以上三种情形都有可能
答案:A
如图,∵M、N分别为A1A和A1B1中点,
∴MN∥AB1,
又∵P是正方形ABCD的中心,∴P、A、C三点共线,
∴AB1?平面PB1C,
∵MN?平面PB1C,∴MN∥平面PB1C.
练习3:在正方体ABCD-A1B1C1D1中和平面C1DB平行的侧面对角线有________条.
答案:3
例2: 如图,已知E、F分别是三棱锥A-BCD的侧棱AB、AD的中点,求证:EF∥平面BCD.
解析:找到平面BCD中与EF平行的直线,即可由定理证明结论.
答案:证明:∵E、F分别是AB、AD的中点,∴EF∥BD.
又∵EF?平面BCD,BD?平面BCD,
∴EF∥平面BCD.
练习1: 如图所示,已知P是?ABCD所在平面外的一点,M是PB的中点,求证:PD∥平面MAC.
答案:连接BD交AC于点O,连接OM.
根据题意,得O是BD的中点,M是PB的中点.
∴在△BPD中,OM是中位线,∴OM∥PD.
又∵OM?平面MAC,PD?平面MAC.
∴PD∥平面MAC.
练习2: 如图,已知正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点,求证:C1O∥平面AB1D1.
答案:连接A1C1交B1D1于点O1,
∵AO∥C1O1,AO=C1O
∴四边形AOC1O1是平行四边形,
∴C1O∥AO1.
又∵C1O?平面AB1D1,
AO1?平面AB1D1,
∴C1O∥平面AB1D1.
例3:已知直线a∥平面α,a∥平面β,α∩β=b,求证a∥b.
解析:若直接证明两条直线a与b平行,则相当困难,注意到线面平行的条件,联想到性质定理,则可想到用构造法作辅助平面来帮助证明.
答案:在平面α上任取一点A,在β上任取一点B,且A、B都不在直线b上.
∵a∥α,a∥β,∴A?a,B?a,
∴由a与A,a与B可分别确定平面γ1,γ2,
设γ1∩α=c,γ2∩β=d,
则a∥c,且a∥d,∴c∥d.
又d?β,且c?β,∴c∥β.
又c?α且α∩β=b,∴c∥b.
而a∥c,∴a∥b.
练习1:三个平面α、β、γ两两相交,
有三条交线l1、l2、l3,如果l1∥l2.求证:l3与l1、l2平行.
答案:如图,α∩β=l1,β∩γ=l2,α∩γ=l3,l1∥l2.
练习2:如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB的中点,过A、N、D三点的平面交PC于点M,求证:AD ∥MN.
答案:∵ABCD为平行四边形,∴AD∥BC,又BC?平面PBC,
AD?平面PBC,∴AD∥平面PBC,
又AD?平面ADMN,平面PBC∩平面ADMN=MN,∴AD∥MN.
类型二 平面与平面平行
例3:如图,在三棱柱ABC-A1B1C1中,E、F、G、H分别是AB、AC、A1B1、A1C1的中点,求证:平面EFA1∥平面BCHG.
解析:运用平面平行的判定.
答案: ∵E、F分别为AB、AC的中点,
∴EF∥BC.
∵EF?平面BCHG,BC?平面BCHG,
∴EF∥平面BCHG.
∵A1GEB,
∴四边形A1EBG是平行四边形,
∴A1E∥GB.
∵A1E?平面BCHG,GB?平面BCHG,
∴A1E∥平面BCHG.
∵A1E∩EF=E,∴平面EFA1∥平面BCHG.
练习1:如图所示,已知正方体ABCD-A1B1C1D1,
求证:平面AB1D1∥平面BDC1.
答案: ∵ABA1B1,C1D1A1B1,∴ABC1D1.
∴四边形ABC1D1为平行四边形.
∴AD1∥BC1.
又AD1?平面AB1D1,BC1?平面AB1D1,
∴BC1∥平面AB1D1.
同理BD∥平面AB1D1.
又∵BD∩BC1=B,∴平面AB1D1∥平面BDC1.
练习2:已知正方体ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,求证:平面BDF∥平面B1D1E.
答案:如图,取BB1的中点G,连接EG、GC1,
则有EGA1B1.
又A1B1C1D1,∴EGC1D1.
∴四边形EGC1D1是平行四边形,
∴D1EGC1.又BGC1F,
∴四边形BGC1F为平行四边形,
∴BF∥C1G,∴BF∥D1E.
又BF?平面B1D1E,D1E?平面B1D1E,
∴BF∥平面B1D1E.
又BD∥B1D1,
同理可得BD∥平面B1D1E.
又∵BF∩BD=B,
∴由平面与平面平行的判定定理得,
平面BDF∥平面B1D1E.
练习3:在正方体EFGH-E1F1G1H1中,平面E1FG1与平面EGH1,平面FHG1与平面F1H1G,平面F1H1H与平面FHE1,平面E1HG1与平面EH1G中互相平行的对数为( )
A.0 B.1
C.2 D.3
答案:本题考查面面平行的判定.∵EG∥E1G1,FG1∥EH1,EG∩EH1=E,E1G1∩FG1=G1,
∴平面EGH1∥平面E1FG1,经验证其他3对均不平行,故选B.
例4:将已知:平面α∥平面β,AB、CD是夹在这两个平面之间的线段,
且点E、G分别为AB、CD的中点,AB不平行于CD,如图所示.
求证:EG∥α,EG∥β.
解析:由平面平行的性质除法得到结论.
答案:如图所示,过点A作AH∥CD,交平面β于点H,
设F是AH的中点,连接HD,则AH綊CD,
∴四边形ACDH为平行四边形.
连接EF、FG和BH,
∵E、F分别是AB、AH的中点,∴EF∥BH.
∵EF?平面β,且BH?平面β,∴EF∥β.
又F、G分别是AH,CD的中点,且AC∥HD,
∴FG∥HD.又∵FG?平面β,HD?平面β,∴FG∥β.
∵EF∩FG=F,∴平面EFG∥β,
又α∥β,∴平面EFG∥α.
∵EG?平面EFC,∴EG∥α,EG∥β.
练习1:知平面α、β、γ,α∥β∥γ,
异面直线l、m分别与平面α、β、γ相交于A、B、C和D、E、F.
求证:=.
答案:连接DC,设DC与平面β相交于G,
则平面ACD与平面α、β分别交于AD、BG,
平面DCF与平面β、γ分别相交于直线GE、CF,
∵α∥β,β∥γ,∴BG∥AD,GE∥CF,
∴=,=,∴=.
练习2:若平面α∥平面β,直线a?α,直线b?β,那么a、b的位置关系是( )
A.无公共点 B.平行
C.既不平行也不相交 D.相交
答案:A
1. 已知直线a、b和平面α,下列命题中正确的是( )
A.若a∥α,b?α,则a∥b
B.若a∥α,b∥α,则a∥b
C.若a∥b,b?α,则a∥α
D.若a∥b,a∥α,则b?α或b∥α
答案:D
2.P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出四个命题:
①OM∥平面PCD;②OM∥平面PBC;③OM∥平面PDA;④OM∥平面PBA.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
答案:B
3.过平面α外的直线l,作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为( )
A.都平行
B.都相交且交于同一点
C.都相交但不一定交于同一点
D.都平行或都交于同一点
答案:D
4.如图,在空间四边形ABCD中,M∈AB,N∈AD,若=,则MN与平面BDC的位置关系是________.
答案: 平行
5.在下列条件中,可判断平面与平面平行的是( )
A、都垂直于 B、内存在不共线的三点到的距离相等
C、是内两条直线,且 D、是两条异面直线,且
答案:D
6. 有下列几个命题:
①平面α内有无数个点到平面β的距离相等,则α∥β;
②α∩γ=a,α∩β=b,且a∥b(α、β、γ分别表示平面,a、b表示直线),则γ∥β;
③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边,则α∥β;
④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行,则α∥β.
其中正确的有________.(填序号)
答案: ③
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1. 已知直线a、b和平面α,下列命题中正确的是( )
A.若a∥α,b?α,则a∥b
B.若a∥α,b∥α,则a∥b
C.若a∥b,b?α,则a∥α
D.若a∥b,a∥α,则b?α或b∥α
答案: D若a∥α,b?α,则a∥b或a与b是异面直线;若a∥α,b∥α,则a与b相交、平行或异面;若a∥b,b?α,则a∥α或a?α,故选D.
2.P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出四个命题:
①OM∥平面PCD;②OM∥平面PBC;③OM∥平面PDA;④OM∥平面PBA.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
答案: B 由已知OM∥PD,∴OM∥平面PCD且OM∥平面PAD.故正确的只有①③,选B.
3.过平面α外的直线l,作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为( )
A.都平行
B.都相交且交于同一点
C.都相交但不一定交于同一点
D.都平行或都交于同一点
答案: D
4..若平面α∥平面β,直线a?α,直线b?β,那么a、b的位置关系是( )
A.无公共点 B.平行
C.既不平行也不相交 D.相交
答案:A
5.若两直线a、b相交,且a∥平面α,则b与α的位置关系是________.
答案:相交或平行
能力提升
6.若平面α∥β,直线a?α,点B∈β,则在β内过点B的所有直线中( )
A.不一定存在与a平行的直线
B.只有两条直线与a平行
C.存在无数条直线与a平行
D.存在惟一一条与a平行的直线
答案:D
7. 已知a是一条直线,过a作平面β,使β∥平面α,这样的β( )
A.只能作一个 B.至少有一个
C.不存在 D.至多有一个
答案:D
8. 已知α∥β,O是两平面外一点,过O作三条直线和平面α交于不在同一直线上的A、B、C三点,和平面β交于A′、B′、C′三点,则△ABC与△A′B′C′的关系是________,若AB=a,A′B′=b,B′C′=c,则BC的长是________.
答案:相似
9. 在正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________________时,有MN∥平面B1BDD1.
答案:M在线段FH上移动
10. 正方体ABCD-A1B1C1D1中,平面AA1C1C和平面BB1D1D的交线与棱CC1的位置关系是________,截面BA1C1和直线AC的位置关系是________.
答案:平行 平行
11. 在正方体ABCD-A1B1C1D1,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点,如图所示.
(1)求证:E、F、B、D四点共面;
(2)求证:平面AMN∥平面EFBD.
答案:(1)分别连接BD、ED、FB,由正方体性质知,B1D1∥BD.
∵E、F分别是C1D1和B1C1的中点,
∴EFB1D1,EFBD.
∴E、F、B、D四点共面.
(2)连接A1C1交MN于P点,交EF于点Q,分别连接PA、QO.∵M、N分别为A1B1、A1D1的中点,
∴MN∥EF,EF?面EFBD,∴MN∥面EFBD.
∵PQAO,∴四边形PAOQ为平行四边形,
∴PA∥QO.而QO?面EFBD,
∵PA∥面EFBD,且PA∩MN=P,PA、MN?面AMN,
∴平面AMN∥面EFBD.
1
