人教版高中数学必修二第四章圆与方程4.3空间直角坐标系(教师版)【优能辅导含答案】
文档属性
| 名称 | 人教版高中数学必修二第四章圆与方程4.3空间直角坐标系(教师版)【优能辅导含答案】 |  | |
| 格式 | zip | ||
| 文件大小 | 896.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 12:26:28 | ||
图片预览



文档简介
空间直角坐标系
__________________________________________________________________________________
__________________________________________________________________________________
通过用类比的数学思想方法得出空间直角坐标系的定义、建立方法、以及空间的点的坐标确定方法;
通过空间中两点的距离解决问题.
一、空间直角坐标系
1. 从空间某一定点引三条互相垂直且有相同单位长度的数轴,这样就建立了
空间直角坐标系.如右图所示.
点叫做坐标原点,、和三轴分别叫做横、纵轴和竖轴,通过每
两个轴的平面叫做坐标平面,分别称为平面、平面、平面.
通常建立的坐标系为右手直角坐标系,即右手拇指指向轴的正方向,
食指指向轴的正方向,中指指向轴的正方向.
2.空间特殊平面与特殊直线:
每两条坐标轴分别确定的平面yOz、xOz、xOy,叫做坐标平面.
xOy平面(通过x轴和y轴的平面)是坐标形如(x,y,0)的点构成的点集,其中x,y为任意的实数;
xOz平面(通过x轴和z轴的平面)是坐标形如(x,0,z )的点构成的点集,其中x,z为任意的实数;
yOz平面(通过y轴和z轴的平面)是坐标形如(0,y,z)的点构成的点集,其中y,z为任意的实数;
x轴是坐标形如(x,0,0)的点构成的点集,其中x为任意实数;
y轴是坐标形如(0,y,0)的点构成的点集,其中y为任意实数;
z轴是坐标形如(0,0,z)的点构成的点集,其中z为任意实数.
3.空间结构:
三个坐标平面把空间分为八部分,每一部分称为一个卦限.在坐标平面xOy上方,分别对应该坐标平面上四个象限的卦限,称为第Ⅰ、第Ⅱ、第Ⅲ、第Ⅳ卦限;在下方的卦限称为第Ⅴ、第Ⅵ、第Ⅶ、第Ⅷ卦限.
二、关于一些对称点的坐标求法
1.关于坐标平面对称
2.关于坐标轴对称
三、空间两点间的距离公式
一般地,空间中任意两点间的距离为
特殊地,任一点到原点的距离为
类型一 空间点的坐标
例1:已知棱长为2的正方体ABCD-A′B′C′D′,建立如图所示不同的空间直角坐标系,试分别写出正方体各顶点的坐标.
解析:由空间直角坐标系定义求解
答案:①对于图一,因为D是坐标原点,A、C、D′分别在x轴、y轴、z轴的正半轴上,又正方体的棱长为2,所以D(0,0,0)、A(2,0,0)、C(0,2,0)、D′(0,0,2).
因为B点在xDy平面上,它在x轴、y轴上的射影分别为A、C,所以B(2,2,0).
同理,A′(2,0,2)、C′(0,2,2).
因为B′在xDy平面上的射影是B,在z轴上的射影是D′,所以B′(2,2,2).
②对于图二,A、B、C、D都在xD′y平面的下方,所以其z坐标都是负的,A′、B′、C′、D′都在xD′y平面上,所以其z坐标都是零.因为D′是坐标原点,A′,C′分别在x轴、y轴的正半轴上,D在z轴的负半轴上,且正方体的棱长为2,所以D′(0,0,0)、A′(2,0,0)、C′(0,2,0)、D(0,0,-2).
同①得B′(2,2,0)、A(2,0,-2)、C(0,2,-2)、B(2,2,-2).
练习1:如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点,棱长为1,求E、F点的坐标.
答案:建立如图所示的空间直角坐标系.
E点在xOy面上的射影为B(1,1,0),
且z坐标为,∴E.
F点在xOy面上的射影为BD的中点G,
G,且z坐标为1,∴F.
练习2:点(2,0,3)位于( )
A.y轴上 B.x轴上
C.xOz平面内 D.yOz平面内
答案:C
例2:已知V-ABCD为正四棱锥,O为底面中心,AB=2,VO=3,试建立空间直角坐标系,并求出各顶点的坐标.
解析:本题中由于所给几何体是正四棱锥,故建系方法比较灵活,除答案所给方案外,也可以正方形ABCD的任一顶点为原点,以交于这一顶点的两条边所在直线分别为x轴、y轴建系.如以A为顶点AB、AD所在直线分别为x轴、y轴建系,等等.
答案:因为所给几何体为正四棱锥,其底面为正方形,对角线相互垂直,故以O为原点,互相垂直的对角线AC、BD所在直线为x轴、y轴,OV为z轴建立如图所示坐标系.
∵正方形ABCD边长AB=2,
∴AO=OC=OB=OD=,又VO=3,
∴A(0,-,0),B(,0,0),C(0,,0),
D(-,0,0),V(0,0,3).
练习1:如图所示,棱长为a的正方体OABC-D′A′B′C′中,对角线OB′与BD′相交于点Q,顶点O为坐标原点,OA、OC分别在x轴、y轴的正半轴上,试写出点Q的坐标.
答案:∵OB′与BD′相交于Q点,
∴Q点在xOy平面内的投影应为OB与AC的交点,
∴Q点坐标为.
同理可知Q点在xOz平面内的投影也应为AD′与OA′的并点,
∴Q点坐标为.
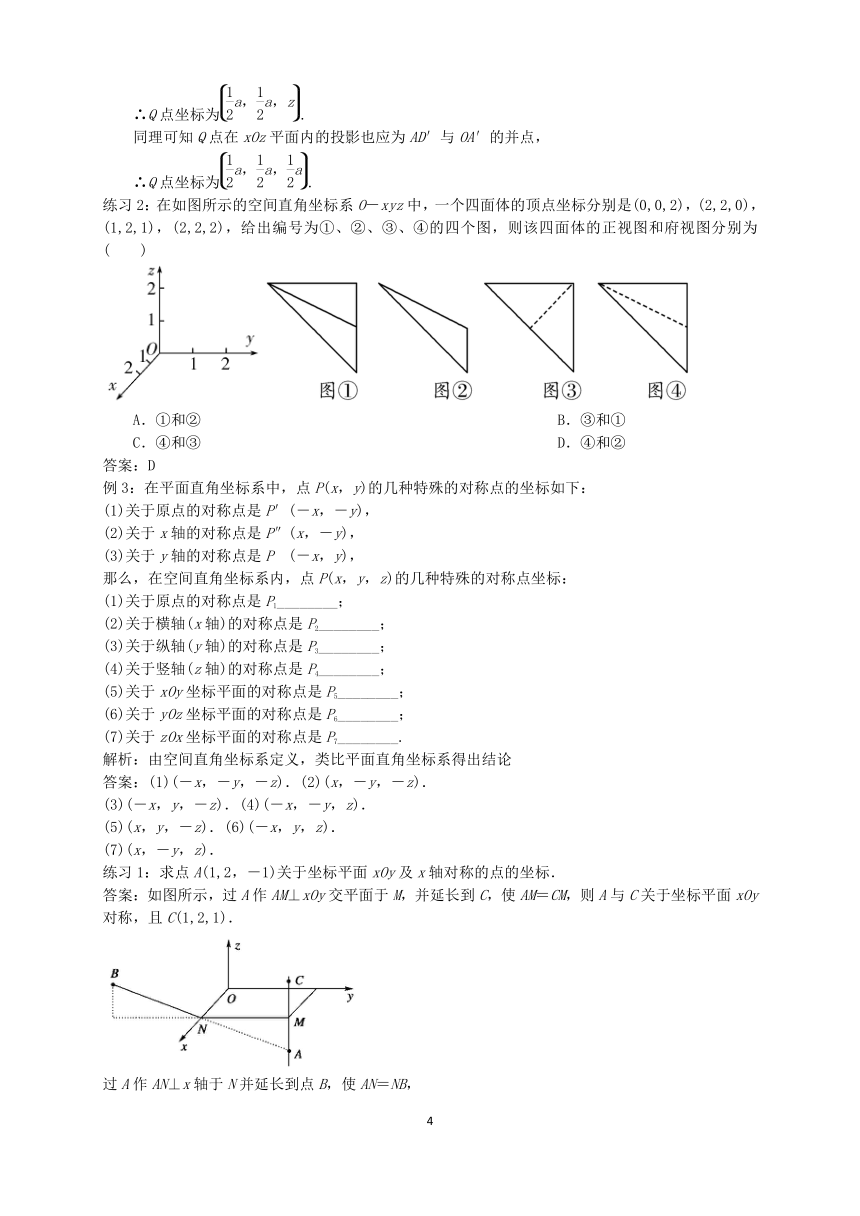
练习2:在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号为①、②、③、④的四个图,则该四面体的正视图和府视图分别为( )
A.①和② B.③和①
C.④和③ D.④和②
答案:D
例3:在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:
(1)关于原点的对称点是P′(-x,-y),
(2)关于x轴的对称点是P″(x,-y),
(3)关于y轴的对称点是Px,y),
那么,在空间直角坐标系内,点P(x,y,z)的几种特殊的对称点坐标:
(1)关于原点的对称点是P1________;
(2)关于横轴(x轴)的对称点是P2________;
(3)关于纵轴(y轴)的对称点是P3________;
(4)关于竖轴(z轴)的对称点是P4________;
(5)关于xOy坐标平面的对称点是P5________;
(6)关于yOz坐标平面的对称点是P6________;
(7)关于zOx坐标平面的对称点是P7________.
解析:由空间直角坐标系定义,类比平面直角坐标系得出结论
答案:(1)(-x,-y,-z).(2)(x,-y,-z).
(3)(-x,y,-z).(4)(-x,-y,z).
(5)(x,y,-z).(6)(-x,y,z).
(7)(x,-y,z).
练习1:求点A(1,2,-1)关于坐标平面xOy及x轴对称的点的坐标.
答案:如图所示,过A作AM⊥xOy交平面于M,并延长到C,使AM=CM,则A与C关于坐标平面xOy对称,且C(1,2,1).
过A作AN⊥x轴于N并延长到点B,使AN=NB,
则A与B关于x轴对称,且B(1,-2,1).
∴A(1,2,-1)关于坐标平面xOy对称的点C(1,2,1);
A(1,2,-1)关于x轴对称的点B(1,-2,1).
练习2:点关于坐标平面对称点的坐标是( )
A. B. C. D.
答案:B
类型二 空间两点间距离公式
例4:证明以A(4,3,1)、B(7,1,2)、C(5,2,3)为顶点的△ABC是等腰三角形.
解析:运用两点间距离公式
答案: 由两点间距离公式:
|AB|==,
|BC|==,
|AC|==,
∵|BC|=|AC|,∴△ABC为等腰三角形.
练习1:求下列两点间的距离.
(1)A(-1,-2,3)、B(3,0,1);
(2)M(0,-1,0)、N(-3,0,4).
答案:(1)d(A,B)==2.
(2)d(M,N)==.
练习2:2.点P(a,b,c)到坐标平面xOy的距离是( )
A.|a| B.|b|
C.|c| D.以上都不对
答案:C
例5:如图所示,在河的一侧有一塔CD=5m,河宽BC=3m,另一侧有点A,AB=4m,求点A与塔顶D的距离AD.
解析:建立合适的空间直角坐标系解决问题
答案:以塔底C为坐标原点建立如下图所示的坐标系.
则D(0,0,5),A(3,-4,0),
∴d(A,D)==5,
即点A与塔顶D的距离为5m.
练习1:已知空间三点A(1,2,4)、B(2,4,8)、C(3,6,12),求证A、B、C三点在同一条直线上.
答案:d(A,B)==,
d(B,C)==,
d(A,C)==2,
∴AB+BC=AC,故A、B、C三点共线.
练习2:以三点为顶点的三角形是( C )
A.直角三角形 B.钝角三角形 C.等腰直角三角形 D.等腰三角形
答案:C
例6:求到两点A(2,3,0)、B(5,1,0)距离相等的点P的坐标满足的条件.
解析:运用两点间距离公式.
答案:设P(x,y,z),
则PA=,
PB=.
∵PA=PB,
∴=.
化简得6x-4y-13=0.
∴点P的坐标满足的条件为6x-4y-13=0.
练习1:若点P(x,y,z)到A(1,0,1)、B(2,1,0)两点的距离相等,则x,y,z满足的关系式是____________;
答案:2x+2y-2z-3=0
练习2:若点A(2,1,4)与点P(x,y,z)的距离为5,则x、y、z满足的关系式是____________;
答案:(x-2)2+(y-1)2+(z-4)2=25
练习3:已知空间两点A(-3,-1,1)、B(-2,2,3)在Oz轴上有一点C,它与A、B两点的距离相等,则C点的坐标是____________.
答案:
1.下列说法:
①在空间直角坐标系中,在x轴上的点的坐标一定可记为(0,b,c);
②在空间直角坐标系中,在yOz平面上的点的坐标一定可记为(0,b,c);
③在空间直角坐标系中,在z轴上的点的坐标一定可记为(0,0,c);
④在空间直角坐标系中,在xOz平面上的点的坐标一定可记为(a,0,c).
其中正确的个数是( )
A.1 B.2
C.3 D.4
答案:C
2.在空间直角坐标系Oxyz中,点(3,4,-5)关于z轴对称的点的坐标是( )
A.(-3,-4,5) B.(-3,-4,-5)
C.(-3,4,5) D.(3,4,5)
答案: B
3.设点B是点A(2,-3,5)关于xOy坐标平面的对称点,则|AB|等于( )
A.10 B.
C. D.38
答案:A
4.已知三点A(-1,0,1)、B(2,4,3)、C(5,8,5),则( )
A.三点构成等腰三角形
B.三点构成直角三角形
C.三点构成等腰直角三角形
D.三点构不成三角形
答案:D
5.点(1,1,-2)关于yOz平面的对称点的坐标是________.
答案:(-1,1,-2)
6.空间直角坐标系中的点A(2,3,5)与B(3,1,4)之间的距离是________.
答案:
7. 在空间直角坐标系中,点M(-2,4,-3)在xOz平面上的射影为M′点,则M′关于原点对称点的坐标是________.
答案:(2,0,3)
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1.点P(-1,2,0)位于( )
A.y轴上 B.z轴上
C.xOy平面上 D.xOz平面上
答案:C
2.点P(-1,2,3)关于xOy坐标平面对称点的坐标是( )
A.(1,2,3) B.(-1,-2,3)
C.(-1,2,-3) D.(1,-2,-3)
答案:C
3.已知A(1,0,2)、B(1,-3,1),点M在z轴上且到A、B两点的距离相等,则M点坐标为( )
A.(-3,0,0) B.(0,-3,0)
C.(0,0,-3) D.(0,0,3)
答案:C
4.已知正方体的每条棱都平行于坐标轴,两个顶点为A(-6,-6,-6)、B(8,8,8),且两点不在正方体的同一个面上,正方体的对角线长为( )
A.14 B.3
C.5 D.42
答案:A
5.已知一长方体ABCD-A1B1C1D1的对称中心在坐标原点O,交于同一顶点的三个面分别平行于三个坐标平面,其中顶点A1、B1、C1、D1分别位于第Ⅰ、Ⅱ、Ⅲ、Ⅳ卦限,且棱长AA1=2,AB=6,AD=4.求长方体各顶点的坐标.
答案:由题意,可建立如图所示的空间直角坐标系O-xyz,
∴A1(3,2,1)、B1(-3,2,1)、C1(-3,-2,1)、D1(3,-2,1),A(3,2,-1)、B(-3,2,-1)、
C(-3,-2,-1)、D(3,-2,-1).
能力提升
6.点A(-3,1,5)、B(4,3,1)的中点坐标是( )
A. B.
C. D.
答案 B
7. 以正方体ABCD-A1B1C1D1的棱AB、AD、AA1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1的中点的坐标为( )
A. B.
C. D.
答案:C
8. 点M(2,-3,5)到x轴的距离d等于( )
A. B.
C. D.
答案:B
9. 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.试建立适当的坐标系,写出点B、C、E、A1的坐标.
答案:以D为坐标原点,射线DA为x轴的正半轴,建立如图所示的空间直角坐标Dxyz.依题设,B(2,2,0)、C(0,2,0)、E(0,2,1)、A1(2,0,4).
10. 在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C中点,求M、N两点间的距离.
答案:建立如图所示空间直角坐标系,据题设条件有:
|A1C1|=2,
∵|MC1|=2|A1M|,
∴|A1M|=,
∴M(,,4).
又C(2,2,0),D1(0,2,4),N为CD1中点∴N(1,2,2),∴|MN|==.
7
__________________________________________________________________________________
__________________________________________________________________________________
通过用类比的数学思想方法得出空间直角坐标系的定义、建立方法、以及空间的点的坐标确定方法;
通过空间中两点的距离解决问题.
一、空间直角坐标系
1. 从空间某一定点引三条互相垂直且有相同单位长度的数轴,这样就建立了
空间直角坐标系.如右图所示.
点叫做坐标原点,、和三轴分别叫做横、纵轴和竖轴,通过每
两个轴的平面叫做坐标平面,分别称为平面、平面、平面.
通常建立的坐标系为右手直角坐标系,即右手拇指指向轴的正方向,
食指指向轴的正方向,中指指向轴的正方向.
2.空间特殊平面与特殊直线:
每两条坐标轴分别确定的平面yOz、xOz、xOy,叫做坐标平面.
xOy平面(通过x轴和y轴的平面)是坐标形如(x,y,0)的点构成的点集,其中x,y为任意的实数;
xOz平面(通过x轴和z轴的平面)是坐标形如(x,0,z )的点构成的点集,其中x,z为任意的实数;
yOz平面(通过y轴和z轴的平面)是坐标形如(0,y,z)的点构成的点集,其中y,z为任意的实数;
x轴是坐标形如(x,0,0)的点构成的点集,其中x为任意实数;
y轴是坐标形如(0,y,0)的点构成的点集,其中y为任意实数;
z轴是坐标形如(0,0,z)的点构成的点集,其中z为任意实数.
3.空间结构:
三个坐标平面把空间分为八部分,每一部分称为一个卦限.在坐标平面xOy上方,分别对应该坐标平面上四个象限的卦限,称为第Ⅰ、第Ⅱ、第Ⅲ、第Ⅳ卦限;在下方的卦限称为第Ⅴ、第Ⅵ、第Ⅶ、第Ⅷ卦限.
二、关于一些对称点的坐标求法
1.关于坐标平面对称
2.关于坐标轴对称
三、空间两点间的距离公式
一般地,空间中任意两点间的距离为
特殊地,任一点到原点的距离为
类型一 空间点的坐标
例1:已知棱长为2的正方体ABCD-A′B′C′D′,建立如图所示不同的空间直角坐标系,试分别写出正方体各顶点的坐标.
解析:由空间直角坐标系定义求解
答案:①对于图一,因为D是坐标原点,A、C、D′分别在x轴、y轴、z轴的正半轴上,又正方体的棱长为2,所以D(0,0,0)、A(2,0,0)、C(0,2,0)、D′(0,0,2).
因为B点在xDy平面上,它在x轴、y轴上的射影分别为A、C,所以B(2,2,0).
同理,A′(2,0,2)、C′(0,2,2).
因为B′在xDy平面上的射影是B,在z轴上的射影是D′,所以B′(2,2,2).
②对于图二,A、B、C、D都在xD′y平面的下方,所以其z坐标都是负的,A′、B′、C′、D′都在xD′y平面上,所以其z坐标都是零.因为D′是坐标原点,A′,C′分别在x轴、y轴的正半轴上,D在z轴的负半轴上,且正方体的棱长为2,所以D′(0,0,0)、A′(2,0,0)、C′(0,2,0)、D(0,0,-2).
同①得B′(2,2,0)、A(2,0,-2)、C(0,2,-2)、B(2,2,-2).
练习1:如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点,棱长为1,求E、F点的坐标.
答案:建立如图所示的空间直角坐标系.
E点在xOy面上的射影为B(1,1,0),
且z坐标为,∴E.
F点在xOy面上的射影为BD的中点G,
G,且z坐标为1,∴F.
练习2:点(2,0,3)位于( )
A.y轴上 B.x轴上
C.xOz平面内 D.yOz平面内
答案:C
例2:已知V-ABCD为正四棱锥,O为底面中心,AB=2,VO=3,试建立空间直角坐标系,并求出各顶点的坐标.
解析:本题中由于所给几何体是正四棱锥,故建系方法比较灵活,除答案所给方案外,也可以正方形ABCD的任一顶点为原点,以交于这一顶点的两条边所在直线分别为x轴、y轴建系.如以A为顶点AB、AD所在直线分别为x轴、y轴建系,等等.
答案:因为所给几何体为正四棱锥,其底面为正方形,对角线相互垂直,故以O为原点,互相垂直的对角线AC、BD所在直线为x轴、y轴,OV为z轴建立如图所示坐标系.
∵正方形ABCD边长AB=2,
∴AO=OC=OB=OD=,又VO=3,
∴A(0,-,0),B(,0,0),C(0,,0),
D(-,0,0),V(0,0,3).
练习1:如图所示,棱长为a的正方体OABC-D′A′B′C′中,对角线OB′与BD′相交于点Q,顶点O为坐标原点,OA、OC分别在x轴、y轴的正半轴上,试写出点Q的坐标.
答案:∵OB′与BD′相交于Q点,
∴Q点在xOy平面内的投影应为OB与AC的交点,
∴Q点坐标为.
同理可知Q点在xOz平面内的投影也应为AD′与OA′的并点,
∴Q点坐标为.
练习2:在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号为①、②、③、④的四个图,则该四面体的正视图和府视图分别为( )
A.①和② B.③和①
C.④和③ D.④和②
答案:D
例3:在平面直角坐标系中,点P(x,y)的几种特殊的对称点的坐标如下:
(1)关于原点的对称点是P′(-x,-y),
(2)关于x轴的对称点是P″(x,-y),
(3)关于y轴的对称点是Px,y),
那么,在空间直角坐标系内,点P(x,y,z)的几种特殊的对称点坐标:
(1)关于原点的对称点是P1________;
(2)关于横轴(x轴)的对称点是P2________;
(3)关于纵轴(y轴)的对称点是P3________;
(4)关于竖轴(z轴)的对称点是P4________;
(5)关于xOy坐标平面的对称点是P5________;
(6)关于yOz坐标平面的对称点是P6________;
(7)关于zOx坐标平面的对称点是P7________.
解析:由空间直角坐标系定义,类比平面直角坐标系得出结论
答案:(1)(-x,-y,-z).(2)(x,-y,-z).
(3)(-x,y,-z).(4)(-x,-y,z).
(5)(x,y,-z).(6)(-x,y,z).
(7)(x,-y,z).
练习1:求点A(1,2,-1)关于坐标平面xOy及x轴对称的点的坐标.
答案:如图所示,过A作AM⊥xOy交平面于M,并延长到C,使AM=CM,则A与C关于坐标平面xOy对称,且C(1,2,1).
过A作AN⊥x轴于N并延长到点B,使AN=NB,
则A与B关于x轴对称,且B(1,-2,1).
∴A(1,2,-1)关于坐标平面xOy对称的点C(1,2,1);
A(1,2,-1)关于x轴对称的点B(1,-2,1).
练习2:点关于坐标平面对称点的坐标是( )
A. B. C. D.
答案:B
类型二 空间两点间距离公式
例4:证明以A(4,3,1)、B(7,1,2)、C(5,2,3)为顶点的△ABC是等腰三角形.
解析:运用两点间距离公式
答案: 由两点间距离公式:
|AB|==,
|BC|==,
|AC|==,
∵|BC|=|AC|,∴△ABC为等腰三角形.
练习1:求下列两点间的距离.
(1)A(-1,-2,3)、B(3,0,1);
(2)M(0,-1,0)、N(-3,0,4).
答案:(1)d(A,B)==2.
(2)d(M,N)==.
练习2:2.点P(a,b,c)到坐标平面xOy的距离是( )
A.|a| B.|b|
C.|c| D.以上都不对
答案:C
例5:如图所示,在河的一侧有一塔CD=5m,河宽BC=3m,另一侧有点A,AB=4m,求点A与塔顶D的距离AD.
解析:建立合适的空间直角坐标系解决问题
答案:以塔底C为坐标原点建立如下图所示的坐标系.
则D(0,0,5),A(3,-4,0),
∴d(A,D)==5,
即点A与塔顶D的距离为5m.
练习1:已知空间三点A(1,2,4)、B(2,4,8)、C(3,6,12),求证A、B、C三点在同一条直线上.
答案:d(A,B)==,
d(B,C)==,
d(A,C)==2,
∴AB+BC=AC,故A、B、C三点共线.
练习2:以三点为顶点的三角形是( C )
A.直角三角形 B.钝角三角形 C.等腰直角三角形 D.等腰三角形
答案:C
例6:求到两点A(2,3,0)、B(5,1,0)距离相等的点P的坐标满足的条件.
解析:运用两点间距离公式.
答案:设P(x,y,z),
则PA=,
PB=.
∵PA=PB,
∴=.
化简得6x-4y-13=0.
∴点P的坐标满足的条件为6x-4y-13=0.
练习1:若点P(x,y,z)到A(1,0,1)、B(2,1,0)两点的距离相等,则x,y,z满足的关系式是____________;
答案:2x+2y-2z-3=0
练习2:若点A(2,1,4)与点P(x,y,z)的距离为5,则x、y、z满足的关系式是____________;
答案:(x-2)2+(y-1)2+(z-4)2=25
练习3:已知空间两点A(-3,-1,1)、B(-2,2,3)在Oz轴上有一点C,它与A、B两点的距离相等,则C点的坐标是____________.
答案:
1.下列说法:
①在空间直角坐标系中,在x轴上的点的坐标一定可记为(0,b,c);
②在空间直角坐标系中,在yOz平面上的点的坐标一定可记为(0,b,c);
③在空间直角坐标系中,在z轴上的点的坐标一定可记为(0,0,c);
④在空间直角坐标系中,在xOz平面上的点的坐标一定可记为(a,0,c).
其中正确的个数是( )
A.1 B.2
C.3 D.4
答案:C
2.在空间直角坐标系Oxyz中,点(3,4,-5)关于z轴对称的点的坐标是( )
A.(-3,-4,5) B.(-3,-4,-5)
C.(-3,4,5) D.(3,4,5)
答案: B
3.设点B是点A(2,-3,5)关于xOy坐标平面的对称点,则|AB|等于( )
A.10 B.
C. D.38
答案:A
4.已知三点A(-1,0,1)、B(2,4,3)、C(5,8,5),则( )
A.三点构成等腰三角形
B.三点构成直角三角形
C.三点构成等腰直角三角形
D.三点构不成三角形
答案:D
5.点(1,1,-2)关于yOz平面的对称点的坐标是________.
答案:(-1,1,-2)
6.空间直角坐标系中的点A(2,3,5)与B(3,1,4)之间的距离是________.
答案:
7. 在空间直角坐标系中,点M(-2,4,-3)在xOz平面上的射影为M′点,则M′关于原点对称点的坐标是________.
答案:(2,0,3)
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1.点P(-1,2,0)位于( )
A.y轴上 B.z轴上
C.xOy平面上 D.xOz平面上
答案:C
2.点P(-1,2,3)关于xOy坐标平面对称点的坐标是( )
A.(1,2,3) B.(-1,-2,3)
C.(-1,2,-3) D.(1,-2,-3)
答案:C
3.已知A(1,0,2)、B(1,-3,1),点M在z轴上且到A、B两点的距离相等,则M点坐标为( )
A.(-3,0,0) B.(0,-3,0)
C.(0,0,-3) D.(0,0,3)
答案:C
4.已知正方体的每条棱都平行于坐标轴,两个顶点为A(-6,-6,-6)、B(8,8,8),且两点不在正方体的同一个面上,正方体的对角线长为( )
A.14 B.3
C.5 D.42
答案:A
5.已知一长方体ABCD-A1B1C1D1的对称中心在坐标原点O,交于同一顶点的三个面分别平行于三个坐标平面,其中顶点A1、B1、C1、D1分别位于第Ⅰ、Ⅱ、Ⅲ、Ⅳ卦限,且棱长AA1=2,AB=6,AD=4.求长方体各顶点的坐标.
答案:由题意,可建立如图所示的空间直角坐标系O-xyz,
∴A1(3,2,1)、B1(-3,2,1)、C1(-3,-2,1)、D1(3,-2,1),A(3,2,-1)、B(-3,2,-1)、
C(-3,-2,-1)、D(3,-2,-1).
能力提升
6.点A(-3,1,5)、B(4,3,1)的中点坐标是( )
A. B.
C. D.
答案 B
7. 以正方体ABCD-A1B1C1D1的棱AB、AD、AA1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1的中点的坐标为( )
A. B.
C. D.
答案:C
8. 点M(2,-3,5)到x轴的距离d等于( )
A. B.
C. D.
答案:B
9. 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.试建立适当的坐标系,写出点B、C、E、A1的坐标.
答案:以D为坐标原点,射线DA为x轴的正半轴,建立如图所示的空间直角坐标Dxyz.依题设,B(2,2,0)、C(0,2,0)、E(0,2,1)、A1(2,0,4).
10. 在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C中点,求M、N两点间的距离.
答案:建立如图所示空间直角坐标系,据题设条件有:
|A1C1|=2,
∵|MC1|=2|A1M|,
∴|A1M|=,
∴M(,,4).
又C(2,2,0),D1(0,2,4),N为CD1中点∴N(1,2,2),∴|MN|==.
7
