人教版高中数学必修四第1章三角函数1.4三角函数的图像与性质(教师版)【优能辅导含答案】
文档属性
| 名称 | 人教版高中数学必修四第1章三角函数1.4三角函数的图像与性质(教师版)【优能辅导含答案】 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 00:00:00 | ||
图片预览


文档简介
三角函数的图像与性质
__________________________________________________________________________________
__________________________________________________________________________________
一、三角函数的图像:
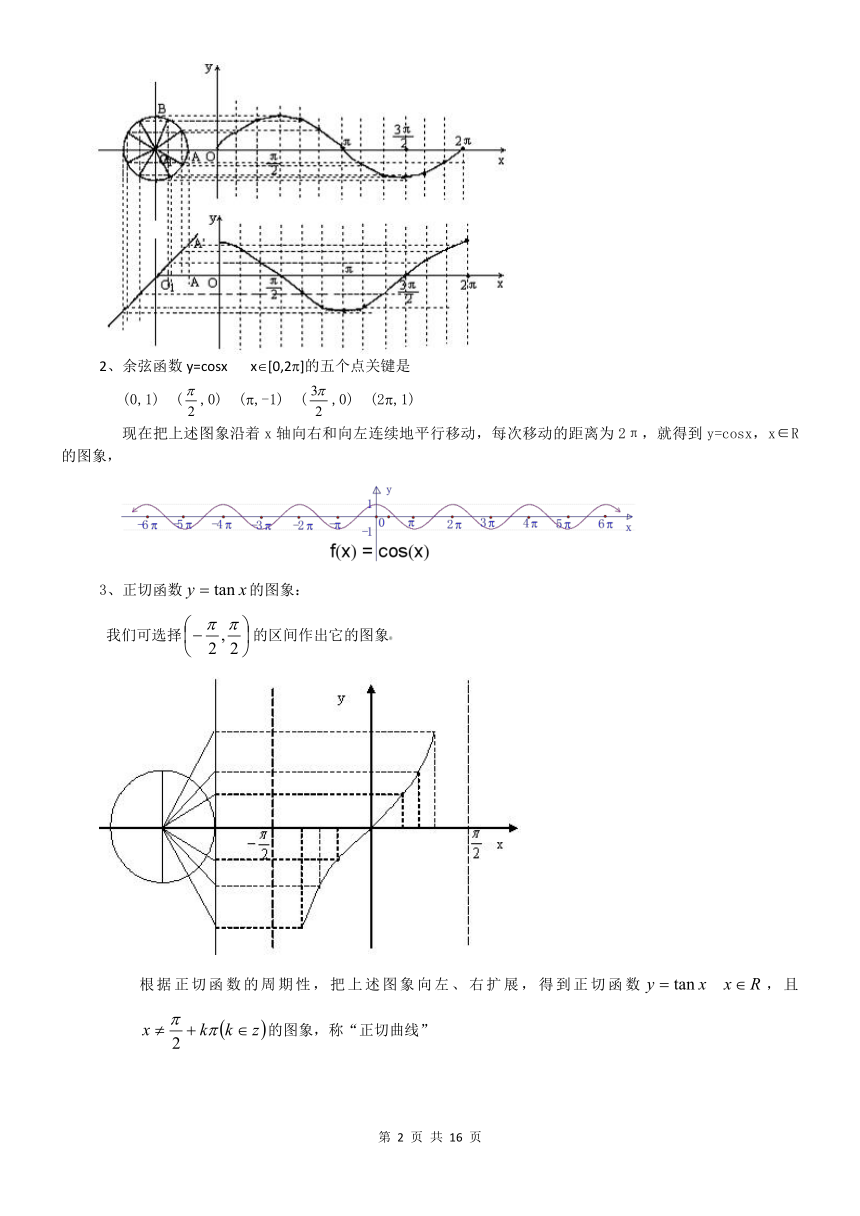
1. 正弦线:设任意角α的终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M,则有,向线段MP叫做角α的正弦线,
2.用单位圆中的正弦线作正弦函数y=sinx,x∈[0,2π]的图象(几何法):
把y=sinx,x∈[0,2π]的图象,沿着x轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx,x∈R叫做正弦曲线
3.用五点法作正弦函数的简图(描点法):
正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:
1、用单位圆中的余弦线作余弦函数的图象(几何法):
为了作三角函数的图象,三角函数的自变量要用弧度制来度量,使自变量与函数值都为实数.在一般情况下,两个坐标轴上所取的单位长度应该相同,否则所作曲线的形状各不相同,从而影响初学者对曲线形状的正确认识.
2、余弦函数y=cosx x?[0,2?]的五个点关键是
(0,1) (,0) (?,-1) (,0) (2?,1)
现在把上述图象沿着x轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=cosx,x∈R的图象,
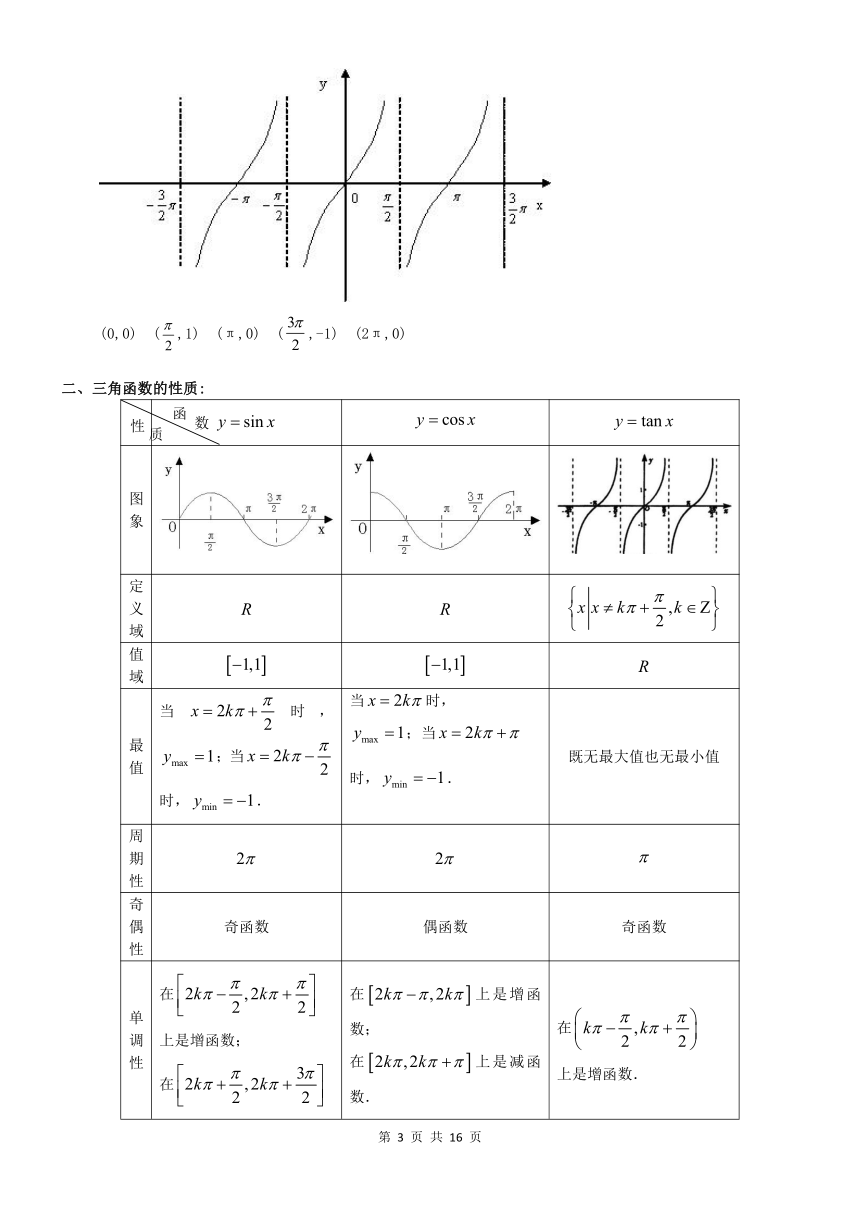
3、正切函数的图象:
我们可选择的区间作出它的图象
根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数,且的图象,称“正切曲线”
(0,0) (,1) (π,0) (,-1) (2π,0)
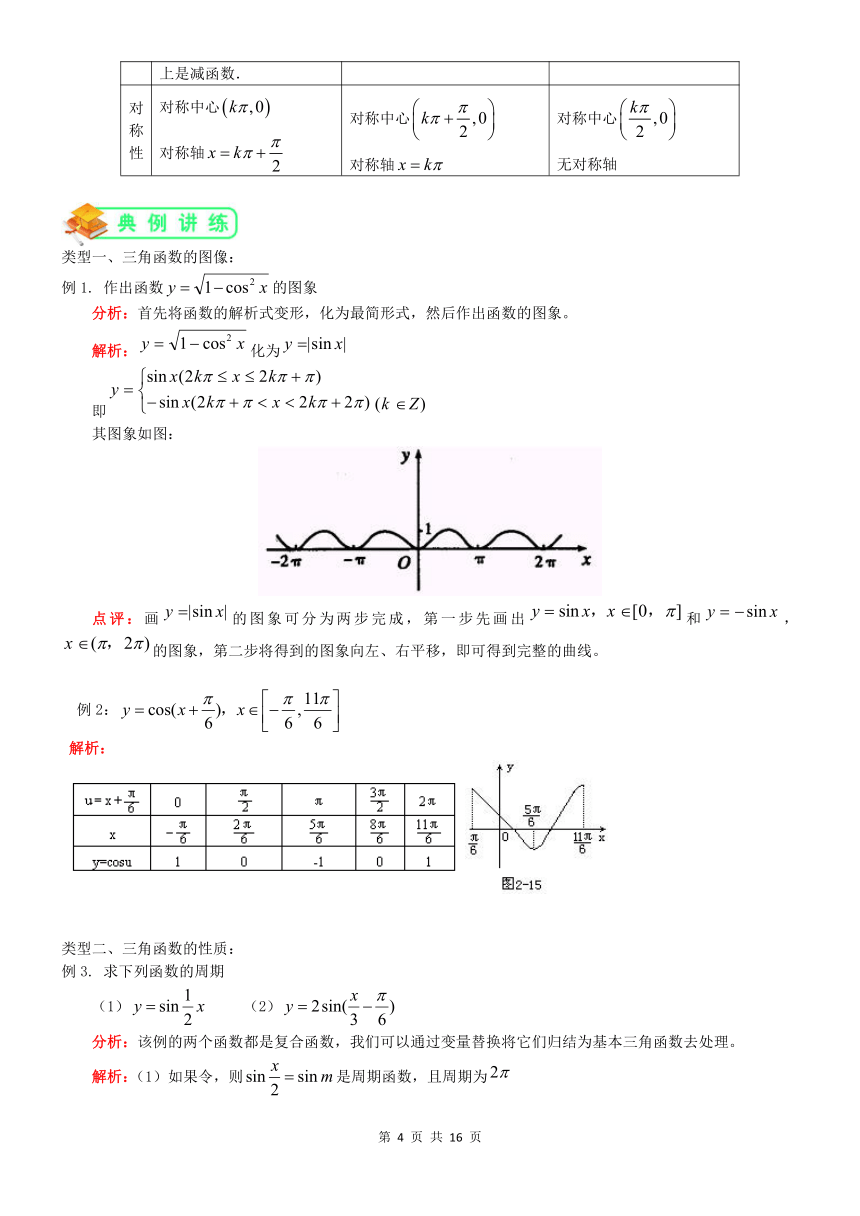
二、三角函数的性质:
图象
定义域
值域
最值 当时,;当 时,. 当时, ;当 时,. 既无最大值也无最小值
周期性
奇偶性 奇函数 偶函数 奇函数
单调性 在 上是增函数; 在 上是减函数. 在上是增函数; 在上是减函数. 在 上是增函数.
对称性 对称中心 对称轴 对称中心 对称轴 对称中心 无对称轴
类型一、三角函数的图像:
例1. 作出函数的图象
分析:首先将函数的解析式变形,化为最简形式,然后作出函数的图象。
解析:化为
即
其图象如图:
点评:画的图象可分为两步完成,第一步先画出和,的图象,第二步将得到的图象向左、右平移,即可得到完整的曲线。
例2:
解析:
类型二、三角函数的性质:
例3. 求下列函数的周期
(1) (2)
分析:该例的两个函数都是复合函数,我们可以通过变量替换将它们归结为基本三角函数去处理。
解析:(1)如果令,则是周期函数,且周期为
即
的周期是
(2)
即
的周期是。
练习:求下列三角函数的周期:
1? y=sin(x+) 2? y=cos2x 3? y=3sin(+) 4? y=tan3x
例:4. 比较下列各组数的大小。
(1)sin194°和cos160°;(2)和;
(3)和
分析:先化为同名函数,然后利用单调性来比较函数值的大小。
解析:(1)
,
从而
即
(2)
又
在[]上是减函数
即
(3)
而在内递增
点评:
(1)比较同名的三角函数值的大小,首先把三角函数转化为同一单调区间上的同名三角函数,利用单调性,由自变量的大小确定函数值的大小。
(2)比较不同名的三角函数的大小时,应先化为同名三角函数,然后再进行比较。
练习:比较下列各组数的大小
(1)sin(-)、sin(-); (2)cos(-)、cos(-).
解:(1)∵-<-<-<. (2)cos(-)=cos=cos
且函数y=sinx,x∈[-,]是增函数 cos(-)=cos=cos
∴sin(-)<sin(-) ∵0<<<π
即sin(-)-sin(-)>0 且函数y=cosx,x∈[0,π]是减函数
∴cos<cos
即cos-cos<0
∴cos(-)-cos(-)<0
例5. 求下列函数的最大值和最小值
(1)
(2)
(3)
分析:可利用sinx与cosx的值域求解,求解过程中要注意自变量的取值范围。
解析:(1)
当时,
当时,
(2)
当时,;
当时,。
(3),
当时,;
当时,。
点评:求三角函数的值域或最大值、最小值问题主要得利用sinx与cosx的有界性,以及复合函数的有关性质。
练习:求下列函数的定义域和值域:
(1) (2) (3)
例6:求函数的定义域、值域,并指出它的周期性、奇偶性、单调性
解:由得,
所求定义域为
值域为R,周期,是非奇非偶函数
在区间上是增函数
例6.求下列函数的单调区间:
(1)y=sin(-);(2)y=-|sin(x+)|。
分析:(1)要将原函数化为y=-sin(x-)再求之。(2)可画出y=-|sin(x+)|的图象。解:(1)y=sin(-)=-sin(-)。
故由2kπ-≤-≤2kπ+。3kπ-≤x≤3kπ+(k∈Z),为单调减区间;由2kπ+≤-≤2kπ+。3kπ+≤x≤3kπ+(k∈Z),为单调增区间。∴递减区间为[3kπ-,3kπ+],
递增区间为[3kπ+,3kπ+](k∈Z)。
(2)y=-|sin(x+)|的图象的增区间为[kπ+,kπ+],减区间为[kπ-,kπ+]。
一、选择题
1.函数y=sinax(a≠0)的最小正周期为π,则a的值为( )
A.2 B.-2
C.±2 D.
[答案] C
[解析] 由题意,得=π,∴a=±2.
2. 函数y=sin(x-)的一条对称轴可以是直线( )
A.x= B.x=
C.x=- D.x=
[答案] B
[解析] 解法一:令x-=kπ+,k∈Z,
∴x=kπ+,k∈Z.
当k=1时,x=,故选B.
解法二:当x=时,y=sin(-)=sin=-1,∴x=是函数y=sin(x-)的一条对称轴.
3.函数y=sin2x的单调减区间是( )
A.(k∈Z) B.(k∈Z)
C.[π+2kπ,3π+2kπ](k∈Z) D.(k∈Z)
[答案] B
[解析] 由2kπ+≤2x≤2kπ+π,k∈Z得
y=sin2x的单调减区间是[kπ+,kπ+π](k∈Z).
4.函数f(x)=x3+sinx+1(x∈R),若f(a)=2,则f(-a)的值为( )
A.3 B.0
C.-1 D.-2
[答案] B
[解析] f(a)=a3+sina+1=2.
f(-a)=-a3-sina+1=-f(a)+2=0.
5. y=sinx-|sinx|的值域是( )
A.[-1,0] B.[0,1]
C.[-1,1] D.[-2,0]
[答案] D
[解析] 当sinx≥0即2kπ≤x≤2kπ+π,k∈Z时,
y=0;
当sinx<0,即2kπ+π
6.已知函数y=1+sinx,x∈[0,2π],则该函数图象与直线y=交点的个数是( )
A.0 B.1
C.2 D.3
[答案] C
[解析] 分别作出函数y=1+sinx,x∈[0,2π]与直线y=的图象,如下图所示:
由图可知,函数y=1+sinx,x∈[0,2π]与直线y=有两个交点,故选C.
二、填空题
7.f(x)是奇函数,当x>0时,f(x)=x2-sinx,则当x<0时,f(x)=________.
[答案] -x2-sinx
[解析] ∵x<0,∴-x>0,
∴f(-x)=(-x)2-sin(-x)=x2+sinx,
∵f(x)为奇函数,∴f(-x)=-f(x),
∴f(x)=-x2-sinx.
8.函数f(x)=cos·cos(+x)是________函数.(奇、偶性)
[答案] 偶函数
[解析] f(x)=sin2xsinx
∵f(-x)=sin(-2x)·sin(-x)
=sin2x·sinx=f(x),
∴f(x)为偶函数.
三、解答题
9.求函数y=7-6sinx-2cos2x的最值.
[解析] y=7-6sinx-2cos2x=2sin2x-6sinx+5
=22+.
由于二次函数y=22+的二次项系数为2>0,所以抛物线开口向上,顶点坐标为.
又sinx∈[-1,1],故当x=2kπ-(k∈Z),即sinx=-1时,y有最大值13;
当x=2kπ+(k∈Z),即sinx=1时,y有最小值1.
_________________________________________________________________________________
_________________________________________________________________________________
基础巩固
1.函数y=5sin的最小正周期是( )
A.π B.π
C.5π D.
[答案] C
[解析] T===5π.
2. 曲线y=sin(2x+)的一条对称轴是( )
A.- B.x=
C.x=- D.x=
[答案] D
[解析] 令2x+=+kπ,k∈Z,
∴x=+,k∈Z.
当k=2时,x=,故选D.
3.下列表示最值是,周期是6π的三角函数的表达式是( )
A.y=sin(+) B.y=sin(3x+)
C.y=2sin(-) D.y=sin(x+)
[答案] A
[解析] 函数y=sin(+)的最大值为,周期为6π,初相为,故选A.
4.下列四个函数中,最小正周期是π且图象关于x=对称的是( )
A.y=sin(+) B.y=sin(2x+)
C.y=sin(2x-) D.y=sin(2x-)
[答案] D
[解析] ∵函数的最小正周期为π,排除A,又∵函数图象关于x=对称,∴当x=时,函数取最大值或最小值,只有选项D满足,故选D.
5.函数y=sin在区间[0,π]内的一个单调递减区间是( )
A. B.
C. D.
[答案] B
[解析] 由+2kπ≤2x+≤+2kπ(k∈Z)
得+kπ≤x≤+kπ(k∈Z),∴选B.
6.设点P是函数f(x)=sinωx的图象C的一个对称中心,若点P到图象C的对称轴的距离的最小值是,则f(x)的最小正周期是( )
A.2π B.π
C. D.
[答案] B
[解析] 由题意知=,∴T=π,故选B.
二、填空题
7.已知函数f(x)=2sin(ωx+φ)的图象如图所示,则f=________.
[答案] 0
[解析] 由图象知,T=,
∵f=0,∴f=f
=f=-f=0.
8.函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ<2π)的部分图象如图,则y=________.
[答案] sin
[解析] =2,∴T=8,ω=,将点(1,1)代入y=sin中得+φ=2kπ+,∵0≤φ<2π,
∴φ=.
三、解答题
9. 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<)的部分图象如图所示,求函数f(x)的解析式.
[解析] 由图象知,周期T=2(-)=π,
所以ω==2.
因为点(,0)在函数图象上,
所以Asin(2×+φ)=0,即sin(+φ)=0.
又因为0<φ<,所以<+φ<.
从而+φ=π,即φ=.
又点(0,1)在函数图象上,所以Asin=1,解得A=2.
故函数f(x)的解析式为f(x)=2sin(2x+).
能力提升
一、选择题
1.若函数f(x)=sin(φ∈[0,2π])是偶函数,则φ=( )
A. B.
C. D.
[答案] C
[解析] 本题考查了三角函数奇偶性,诱导公式.
由y=sin是偶函数知=+kπ,即φ=+3kπ,又∵φ∈[0,2π],∴φ=适合.本题也可用偶函数定义求解.
2.若A、B是钝角△ABC的两个锐角,则点P(cosB-sinA,sinB-cosA)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
[答案] D
[解析] ∵A、B是钝角△ABC的两个锐角,∴A+B<,0
∴sinA
A.[-2,5] B.(-∞,5]
C.[-4,4] D.[0,5]
[答案] C
[解析] 原式可化为:(sinx-2)2=5-a.
∵-1≤sinx≤1,∴1≤(sinx-2)2≤9,
∴1≤5-a≤9,解得a∈[-4,4].
4.函数y=+sinx-sin2x的最大值是( )
A. B.-
C.2 D.不存在
[答案] C
[解析] y=-2+2,
∵-1≤sinx≤1,∴当sinx=时,函数y=-(sinx-)2+2取最大值2.
二、填空题
5.函数y=a+bsinx的最大值是,最小值为-,则a=________,b=________.
[答案] ±1
[解析] 当b>0时,由题意得,
∴.
当b<0时,由题意得,
∴.
6.函数y=sin的单调递减区间为________.
[答案] (k∈Z)
[解析] y=sin=-sin,
函数y=sin的递减区间,
即为函数y′=sin的递增区间,令-+2kπ≤x-≤+2kπ,k∈Z,
得-+2kπ≤x≤+2kπ,k∈Z,
∴函数y=sin(-x+)的单调递减区间为[-+2kπ,+2kπ](k∈Z).
三、解答题
7.已知函数f(x)=sin(2x-),求函数f(x)的最大值及f(x)取最大值时x的取值集合.
[解析] 当2x-=+2kπ,k∈Z时,f(x)取最大值1,此时x=+kπ,k∈Z.
即f(x)的最大值是1,取最大值时x的取值集合为{x|x=+kπ,k∈Z}.
8.用五点法画出函数f(x)=3sin(+)+3在一个周期内的图象.
[解析] 列表如下:
x -
+ 0 π 2π
y 3 6 3 0 3
描点连线:
9.已知函数f(x)=log.
(1)求f(x)的定义域、值域和单调区间;
(2)判断f(x)的奇偶性.
[解析] (1)要使函数有意义,须sin2x>0,
∴2kπ<2x<2kπ+π,
∴kπ
∵0
令y=sin2x,则函数y=sin2x的增区间即为函数f(x)的减区间,函数y=sin2x的减区间即为函数f(x)的增区间.
∴函数f(x)的单调递减区间为(k∈Z),
单调递增区间为(k∈Z).
(2)定义域关于原点不对称,故既不是奇函数,也不是偶函数.
y
x
o
1
-1
函
数
性
质
