人教版高一数学必修三课件:3.3几何概型(共18张PPT)
文档属性
| 名称 | 人教版高一数学必修三课件:3.3几何概型(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 588.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 21:24:15 | ||
图片预览





文档简介
(共18张PPT)
1学习目标
1.了解几何概型与古典概型的区别.
2.理解几何概型的定义及其特点.
3.会用几何概型的概率计算公式求几何概型的概率.
2问题导学
阅读教材p135-136,并思考下列问题:
1.什么叫什么叫几何概率模型?
2. 几何概率的计算公式是什么?
在现实生活中,常常会遇到试验的所有可能结果是无穷多的情况,这时就不能用古典概型来计算事件发生的概率.对此,我们必须学习新的方法来解决这类问题,这就是我们本节课要学习的——几何概型.
某班公交车到终点站的时间可能是11:30~12:00之间的任何一个时刻;往一个方格中投一粒芝麻,芝麻可能落在方格中的任何一点上.这两个试验可能出现的结果是有限个,还是无限个?若没有人为因素,每个试验结果出现的可能性是否相等?
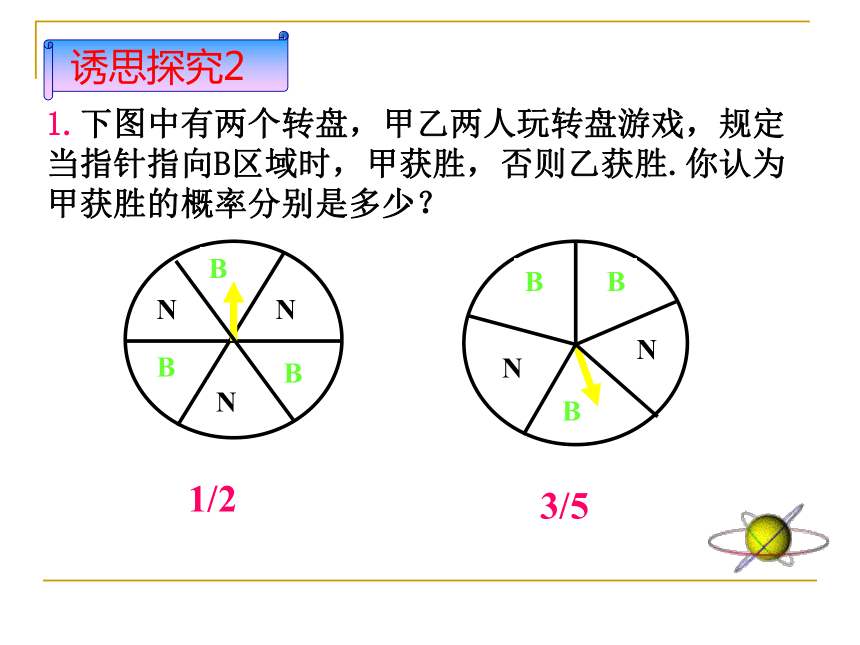
1.下图中有两个转盘,甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜.你认为甲获胜的概率分别是多少?
1/2
3/5
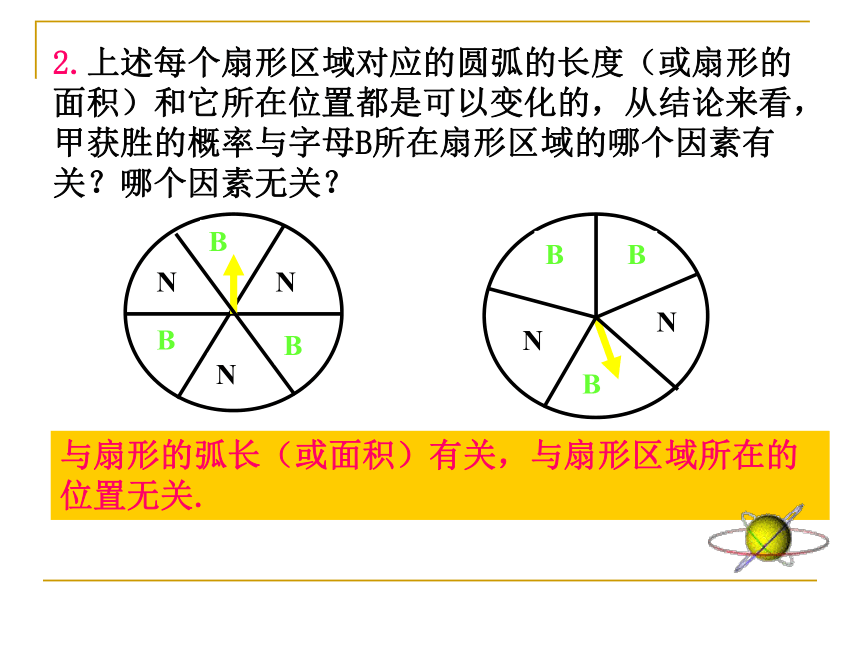
2.上述每个扇形区域对应的圆弧的长度(或扇形的面积)和它所在位置都是可以变化的,从结论来看,甲获胜的概率与字母B所在扇形区域的哪个因素有关?哪个因素无关?
与扇形的弧长(或面积)有关,与扇形区域所在的位置无关.
1.几何概型定义:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概型.
(1)可能出现的结果有无限多个;
(2)每个结果发生的可能性相等.
2.几何概型的特征:
(无限性)
(等可能性)
3.概率公式:
答:等待的时间不超过10分钟的概率为1/6.
某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
解:由题意得:
全部结果所含区域长度:
设他等待的时间不多于10分钟为事件A,则
事件A所含区域长度L=10
∴P(A)=10/60=1/6
在下图的正方形中随机撒一把豆子,如何用随机模拟的方法估计圆周率的值.
解:设正方形的边长为2,则
圆的面积为
正方形的面积为S=2×2=4
假设你家订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到你家,你离开家去工作的时间在早上7:00—8:00之间,问你在离开家前能得到报纸(称为事件A)的概率是多少?
解:如图,设送报人到达的时间为x,你离开家的时间为y,则
全部结果所含区域为正方形
BCDE,其面积为
B
E
G
C
D
事件A所含区域为BFGDE,其面积为
F
答:略
本节课我们学习了几何概型的有关知识:
1.几何概型的特征;
2.几何概型的概率公式;
3.求出几何概型的概率。
4课堂小结:
2.有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.
1.取一根长为3米的绳子,拉直后在任意位置剪断,
那么剪得两段的长都不少于1米的概率有多大?
3.点A为周长等于3的圆周上的一个定点,若在该圆周上随机
取一点B,则劣弧AB的长度小于1的概率为 。
5当堂检测
4.在Rt△ABC中,∠A=30°,过直角顶点C作射线CM交线段AB于M,求使|AM|>|AC|的概率.
解:由题意得:
5.一张方桌的图案如图所示。将一颗豆子
随机地扔到桌面上,假设豆子不落在线上,
求下列事件的概率:
(1)豆子落在红色区域;
(2)豆子落在黄色区域;
(3)豆子落在绿色区域;
(4)豆子落在红色或绿色区域;
(5)豆子落在黄色或绿色区域。
6.甲、乙两人约定在下午4:00~5:00间在某地相见他们约好当
其中一人先到后一定要等另一人15分钟,若另一人仍不到则
可以离去,试求这人能相见的概率。
解:如图,以x为甲到达时间,y为乙到达时间建立坐标系,则
全部结果所含区域为正方形OABC,其面积为
A
C
B
设这两人能相见为事件M,则
事件M所含区域为如图阴影部分,其面积为
7.设关于x的一元二次方程
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取一个数,b是从区间[0,2]任取一个数,求上述方程有实根的概率.
解:由方程 有实根得:
(1)由题意得:全部可能结果有:(0,0)、(0,1)、(0,2)、(1,0)、(1,1)、(1,2)、(2,0)、(2,1)、(2,2)、(3,0)、(3,1)、(3,2),共12种。
设方程有实根为事件A,则事件A含基本事件有: (0,0)、 (1,0)、(1,1)、 (2,0)、(2,1)、(2,2)、(3,0)、(3,1)、(3,2),共9个
∴P(A)=9/12=3/4
答:略
(2)若a是从区间[0,3]任取一个数,b是从区间[0,2]任取一个数,
求上述方程有实根的概率.
解:(2)如图,以a的取值为横轴,b的取值为纵轴建立直角坐标系,则
全部结果所含区域为矩形OABC,
其面积为S=3×2=6
设方程有实根为事件B,则
A
B
C
事件B所含区域面积为
答:上述方程有实根的概率为2/3.
1.下列关于几何概型的说法错误的是 ( )
A.几何概型也是古典概型中的一种
B.几何概型中事件发生的概率与位置、形状无关
C.几何概型中每一个结果的发生具有等可能性
D.几何概型在一次试验中能出现的结果有无限个
2.面积为S的△ABC,D是BC的中点,向△ABC内部投
一点,那么点落在△ABD内的概率为
自学检测
1学习目标
1.了解几何概型与古典概型的区别.
2.理解几何概型的定义及其特点.
3.会用几何概型的概率计算公式求几何概型的概率.
2问题导学
阅读教材p135-136,并思考下列问题:
1.什么叫什么叫几何概率模型?
2. 几何概率的计算公式是什么?
在现实生活中,常常会遇到试验的所有可能结果是无穷多的情况,这时就不能用古典概型来计算事件发生的概率.对此,我们必须学习新的方法来解决这类问题,这就是我们本节课要学习的——几何概型.
某班公交车到终点站的时间可能是11:30~12:00之间的任何一个时刻;往一个方格中投一粒芝麻,芝麻可能落在方格中的任何一点上.这两个试验可能出现的结果是有限个,还是无限个?若没有人为因素,每个试验结果出现的可能性是否相等?
1.下图中有两个转盘,甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜.你认为甲获胜的概率分别是多少?
1/2
3/5
2.上述每个扇形区域对应的圆弧的长度(或扇形的面积)和它所在位置都是可以变化的,从结论来看,甲获胜的概率与字母B所在扇形区域的哪个因素有关?哪个因素无关?
与扇形的弧长(或面积)有关,与扇形区域所在的位置无关.
1.几何概型定义:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概型.
(1)可能出现的结果有无限多个;
(2)每个结果发生的可能性相等.
2.几何概型的特征:
(无限性)
(等可能性)
3.概率公式:
答:等待的时间不超过10分钟的概率为1/6.
某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
解:由题意得:
全部结果所含区域长度:
设他等待的时间不多于10分钟为事件A,则
事件A所含区域长度L=10
∴P(A)=10/60=1/6
在下图的正方形中随机撒一把豆子,如何用随机模拟的方法估计圆周率的值.
解:设正方形的边长为2,则
圆的面积为
正方形的面积为S=2×2=4
假设你家订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到你家,你离开家去工作的时间在早上7:00—8:00之间,问你在离开家前能得到报纸(称为事件A)的概率是多少?
解:如图,设送报人到达的时间为x,你离开家的时间为y,则
全部结果所含区域为正方形
BCDE,其面积为
B
E
G
C
D
事件A所含区域为BFGDE,其面积为
F
答:略
本节课我们学习了几何概型的有关知识:
1.几何概型的特征;
2.几何概型的概率公式;
3.求出几何概型的概率。
4课堂小结:
2.有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.
1.取一根长为3米的绳子,拉直后在任意位置剪断,
那么剪得两段的长都不少于1米的概率有多大?
3.点A为周长等于3的圆周上的一个定点,若在该圆周上随机
取一点B,则劣弧AB的长度小于1的概率为 。
5当堂检测
4.在Rt△ABC中,∠A=30°,过直角顶点C作射线CM交线段AB于M,求使|AM|>|AC|的概率.
解:由题意得:
5.一张方桌的图案如图所示。将一颗豆子
随机地扔到桌面上,假设豆子不落在线上,
求下列事件的概率:
(1)豆子落在红色区域;
(2)豆子落在黄色区域;
(3)豆子落在绿色区域;
(4)豆子落在红色或绿色区域;
(5)豆子落在黄色或绿色区域。
6.甲、乙两人约定在下午4:00~5:00间在某地相见他们约好当
其中一人先到后一定要等另一人15分钟,若另一人仍不到则
可以离去,试求这人能相见的概率。
解:如图,以x为甲到达时间,y为乙到达时间建立坐标系,则
全部结果所含区域为正方形OABC,其面积为
A
C
B
设这两人能相见为事件M,则
事件M所含区域为如图阴影部分,其面积为
7.设关于x的一元二次方程
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取一个数,b是从区间[0,2]任取一个数,求上述方程有实根的概率.
解:由方程 有实根得:
(1)由题意得:全部可能结果有:(0,0)、(0,1)、(0,2)、(1,0)、(1,1)、(1,2)、(2,0)、(2,1)、(2,2)、(3,0)、(3,1)、(3,2),共12种。
设方程有实根为事件A,则事件A含基本事件有: (0,0)、 (1,0)、(1,1)、 (2,0)、(2,1)、(2,2)、(3,0)、(3,1)、(3,2),共9个
∴P(A)=9/12=3/4
答:略
(2)若a是从区间[0,3]任取一个数,b是从区间[0,2]任取一个数,
求上述方程有实根的概率.
解:(2)如图,以a的取值为横轴,b的取值为纵轴建立直角坐标系,则
全部结果所含区域为矩形OABC,
其面积为S=3×2=6
设方程有实根为事件B,则
A
B
C
事件B所含区域面积为
答:上述方程有实根的概率为2/3.
1.下列关于几何概型的说法错误的是 ( )
A.几何概型也是古典概型中的一种
B.几何概型中事件发生的概率与位置、形状无关
C.几何概型中每一个结果的发生具有等可能性
D.几何概型在一次试验中能出现的结果有无限个
2.面积为S的△ABC,D是BC的中点,向△ABC内部投
一点,那么点落在△ABD内的概率为
自学检测
