2.1 圆锥曲线课件18张PPT

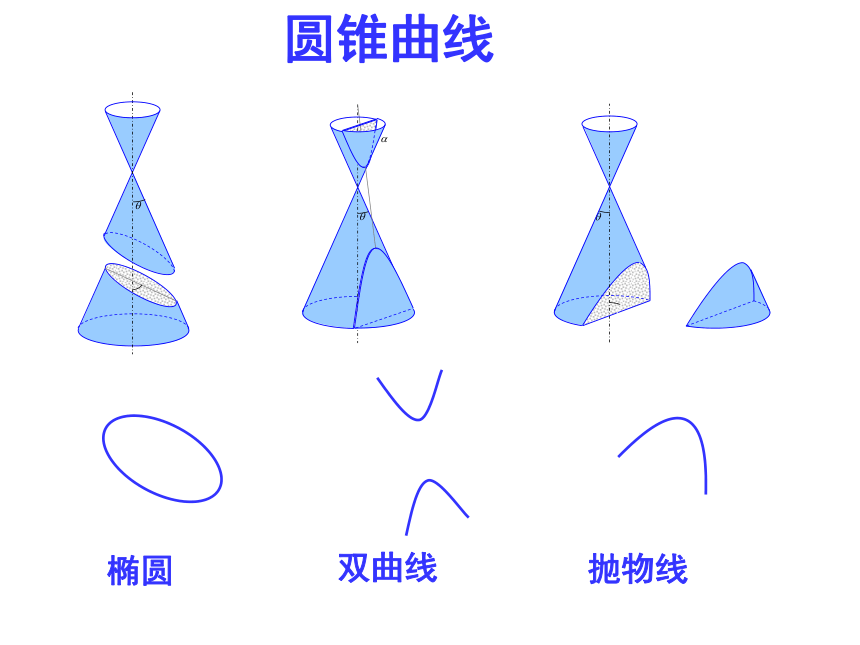
课件18张PPT。圆锥曲线与方程§2.1圆锥曲线嫦娥三号发射视频 在研究今天所学内容之前，我们首先介绍一个曲面——圆锥面。 “圆锥面”可以看成一条直线绕着与它相交的一条直线（两条直线不能垂直）旋转一周所形成的曲面。圆锥面的形成过程 用一个平面去截一个圆锥面，当平面经过圆锥面的顶点时，可得到两条相交直线； 当平面与圆锥面的轴垂直时，截线（平面与圆锥面的交线）是一个圆． 当改变平面的位置时，观察截的图形的变化情况，并思考：
● 用平面截圆锥面还能得到哪些曲线？这些曲线具有哪些几何特征？
平面截圆锥面
椭圆双曲线抛物线圆锥曲线 圆锥曲线有哪些方面的应用？你能举例说明吗？ 圆锥曲线有哪些方面的应用？你能举例说明吗？射门-抛物线
形式进球投篮-抛物线
形式命中 数学家Dandelin在圆锥截面的两侧分别放置一球，使它们都与截面相切（切点分别为F1，F2），又分别与圆锥面的侧面相切（两球与侧面的公共点分别构成圆O1和圆O2）．过M点作圆锥面的一条母线分别交圆O1，圆O2与P，Q两点，MF1 + MF2 ＝MP + MQ ＝ PQ＝定值 因为过球外一点作球的切线长相等，所以
MF1 = MP，MF2 = MQ， 画一画 同学们能不能画一个椭圆？ 椭圆的画法 椭圆的定义: 平面内到两定点 ， 的距离和等于常数（大于 ）的点的轨迹叫做椭圆， 两个定点 ， 叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。 关键信息：距离之和为常数、大于 画双曲线双曲线的定义: 两个定点 ， 叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。 平面内到两定点 ， 的距离的差的绝对值等于常数（小于 ）的点的轨迹叫做双曲线， 关键信息：距离之差的绝对值为常数、小于抛物线的定义 : 平面内到一个定点F和一条定直线L（F不在L上）的距离相等的点轨迹叫做抛物线， 定点F叫做抛物线的焦点，定直线L叫做抛物线的准线 设平面内的动点为M ,有可以用数学表达式来体现: MF=d（d为动点M到直线L的距离） 抛物线的画法CA 【例1】 已知?ABC中，BC长为6，周长为16，那么顶点A在怎样的曲线上运动？ 解：因为AB+AC+BC=16，BC=6，所以AC+AB=10>6=BC，从而顶点A在以B，C为焦点，到两个焦点距离之和等于10的椭圆上运动.CA 训练1 已知?ABC中，B（-3，0），
C（3，0），且AB，BC，AC成等差数列.（1）求证：点A在一个椭圆上运动；
（2）写出这个椭圆的焦点坐标. 训练2 已知?ABC中，BC长为2，∣AB-AC∣=1，那么点A在怎样的曲线上运动？ 训练3 已知经过点A(3，0)的动圆M与直线l：x=-3相切，求动圆圆心M的轨迹.双曲线右支C 【例2】 圆F1在圆F2的内部，且点F1，F2不重合，求证:与圆F1外切，且与圆F2内切的圆的圆心C的轨迹为椭圆.圆F1在圆F2的内部，且点F1，F2不重合，求证:与圆F1外切，且与圆F2内切的圆的圆心C的轨迹为椭圆.图4
解：设圆F1,F2的半径分别为r1,r2,动圆C的半径为t.
根据题意有：CF1=r1+t,CF2=r2-t,消去t有：CF1+CF1=r1+r2(一个大于F1F2的常数)，所以动圆圆心C的轨迹是以F1,F2位焦点的椭圆.D 训练4 如图，已知动圆C与圆F1，F2均外切(圆F1与圆F2相离)，试问:动点C的轨迹是什么曲线?归纳总结平面截圆锥面双球证明理论直观类比圆背景与航天背景注意几何满足的条件