2.3.1 双曲线的标准方程课件38张PPT
文档属性
| 名称 | 2.3.1 双曲线的标准方程课件38张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-09 21:45:15 | ||
图片预览











文档简介
课件38张PPT。老师们,同学们,大家好深圳火炬塔纪念广场巴西利亚大教堂电视塔高中数学 选修2-12.3.1 双曲线的标准方程知识与技能 :掌握双曲线的定义、标准方程及其 推导过程,能根据已知条件求双曲线的标准方程
过程与方法:经历双曲线及其标准方程的获得过程 ,培养学生观察、思考、分析与解决问题的能力,体会分类讨论、类比的数学思想
情感态度与价值观:感受数学的对称美和简洁美,激发学生的学习兴趣学习重点:求双曲线的标准方程 学习难点:正确运用双曲线的定义推导双曲线方程【学习目标、重点、难点】【预学质疑】 问题1、椭圆的定义是什么?【预学质疑】 问题1、椭圆的定义是什么?2a (2a>2c ) PF1 + PF2 =2a( 2a>2c) 【预学质疑】 问题1、椭圆的定义是什么? 焦点在x轴上 焦点在y轴上PF1+PF2=2a( 2a>2c) 【预学质疑】 问题1、椭圆的定义是什么?问题2、将椭圆定义中“和”改为“差”,此时点的轨迹是什么?” 平面内到两个定点F1,F2的距离的差的绝对值
等于常数 2a(小于F1F2的正数)的点的轨迹叫做双曲线 双曲线定义:【解读定义】 符号表示 : |PF1-PF2|=2a 焦 点: 两个定点F1、F2 焦 距: 两焦点之间的距离 F1F2 , 2c 思考
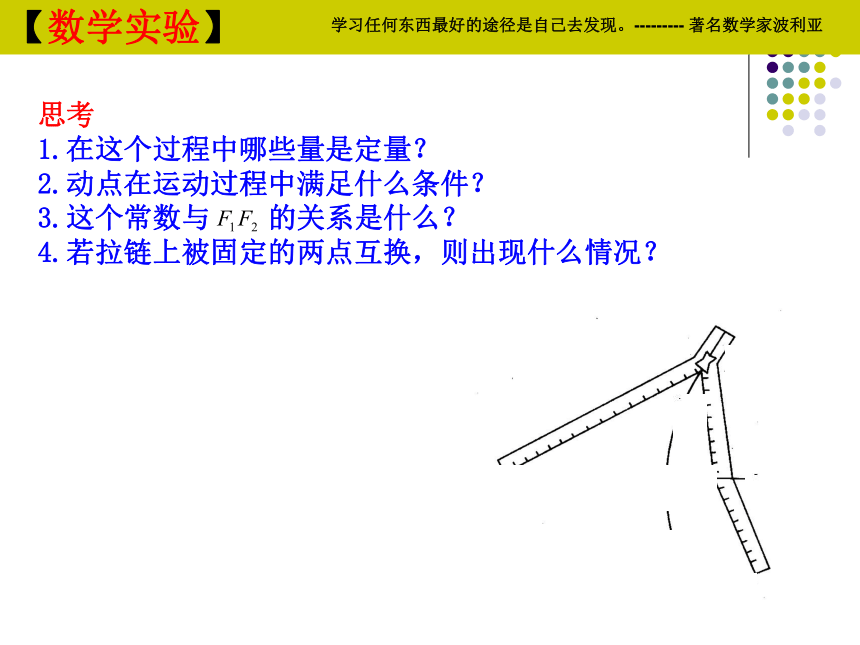
1.在这个过程中哪些量是定量?
2.动点在运动过程中满足什么条件?
3.这个常数与 的关系是什么?
4.若拉链上被固定的两点互换,则出现什么情况?
【数学实验】学习任何东西最好的途径是自己去发现。--------- 著名数学家波利亚P①如图(A),②如图(B),上面 两条合起来叫做双曲线.由①②可得: | PF1-PF2| = 2a
(差的绝对值) PF2-PF1=2a PF1-PF2=2a(双曲线右支)(双曲线左支)PP 平面内到两个定点F1,F2的距离的差的绝对值
等于常数 2a(小于F1F2的正数)的点的轨迹叫做双曲线 双曲线定义:【解读定义】 符号表示 : |PF1-PF2|=2a 焦 点: 两个定点F1、F2 焦 距: 两焦点之间的距离 F1F2 , 2c 平面内到两个定点F1、F2的距离的差的绝对值
等于常数2a(小于F1F2的正数)的点的轨迹叫做双曲线 双曲线定义:【解读定义】 (1)若2a=2c,则轨迹是什么?思考:(2)若2a>2c,则轨迹是什么?(3)若2a=0 ,则轨迹是什么?问题3、如何求双曲线的标准方程?类比 求椭圆标准方程的基本步骤?问题4、焦点在 轴的双曲线的标准方程是什么? 焦点在x轴上, x2项的系数为正;
焦点在y轴上, y2项的系数为正.问题4、焦点在 轴的双曲线的标准方程是什么?确定焦点位置:双曲线看系数正负问题4、焦点在 轴的双曲线的标准方程是什么?确定焦点位置:椭圆看分母大小 双曲线看系数正负双曲线与椭圆之间的区别与联系a>0,b>0,但a不一定大于b, c 2=a2+b2a>b>0,a2=b2+ c 2|PF1-PF2|=2a PF1 + PF2 =2a 双曲线与椭圆之间的区别与联系|PF1-PF2|=2a PF1 + PF2 =2a 双曲线与椭圆之间的区别与联系PF1-PF2=2a PF1 + PF2 =2a ①双曲线“-”号连结,椭圆“+”号连结;例1、
【导学探疑】已知两定点 ,动点 满足 ,求动点 的轨迹方程【规范书写】解:因为 ,
由双曲线的定义可知,点 的轨迹是一条双曲线,焦点在 轴,
设所求双曲线的标准方程为
因为 所以故点 的轨迹方程为 例1、
【导学探疑】已知两定点 ,动点 满足 ,求动点 的轨迹方程变式1、去掉绝对值,求双曲线的标准方程
【规范书写】解:因为 ,
由双曲线的定义可知,点 的轨迹是一条双曲线,焦点在 轴,
设所求双曲线的标准方程为
因为 所以故点 的轨迹方程为 例1、
【导学探疑】已知两定点 ,动点 满足 ,求动点 的轨迹方程变式1、去掉绝对值,求双曲线的标准方程
变式2、 是双曲线上一点满足 ,求 的值【引学释疑】例2、求适合下列条件的双曲线的标准方程
(1) , ,焦点在 轴上(2) 经过点 ,焦点在 轴上 【引学释疑】例2、求适合下列条件的双曲线的标准方程
(1) , ,焦点在 轴上(2) 经过点 ,焦点在 轴上 变式、去掉(1)中焦点在 轴上
【引学释疑】例2、求适合下列条件的双曲线的标准方程
(1) , ,焦点在 轴上(2) 经过点 ,焦点在 轴上 变式、去掉(1)中焦点在 轴上
追踪训练:求适合下列条件的双曲线的标准方程
(1) ,
(2)一个焦点为 ,且过点 固学思疑小结反思
1、数学理论知识2、数学思想方法
双曲线 定义 标准方程类比、分类讨论Thanks for your attention!书 山 有 路 勤 为 径学 海 无 涯 苦 作 舟【课后练习】求适合下列条件的双曲线的标准方程
(1) ,
(2)与双曲线 有相同焦点,且过点
过程与方法:经历双曲线及其标准方程的获得过程 ,培养学生观察、思考、分析与解决问题的能力,体会分类讨论、类比的数学思想
情感态度与价值观:感受数学的对称美和简洁美,激发学生的学习兴趣学习重点:求双曲线的标准方程 学习难点:正确运用双曲线的定义推导双曲线方程【学习目标、重点、难点】【预学质疑】 问题1、椭圆的定义是什么?【预学质疑】 问题1、椭圆的定义是什么?2a (2a>2c ) PF1 + PF2 =2a( 2a>2c) 【预学质疑】 问题1、椭圆的定义是什么? 焦点在x轴上 焦点在y轴上PF1+PF2=2a( 2a>2c) 【预学质疑】 问题1、椭圆的定义是什么?问题2、将椭圆定义中“和”改为“差”,此时点的轨迹是什么?” 平面内到两个定点F1,F2的距离的差的绝对值
等于常数 2a(小于F1F2的正数)的点的轨迹叫做双曲线 双曲线定义:【解读定义】 符号表示 : |PF1-PF2|=2a 焦 点: 两个定点F1、F2 焦 距: 两焦点之间的距离 F1F2 , 2c 思考
1.在这个过程中哪些量是定量?
2.动点在运动过程中满足什么条件?
3.这个常数与 的关系是什么?
4.若拉链上被固定的两点互换,则出现什么情况?
【数学实验】学习任何东西最好的途径是自己去发现。--------- 著名数学家波利亚P①如图(A),②如图(B),上面 两条合起来叫做双曲线.由①②可得: | PF1-PF2| = 2a
(差的绝对值) PF2-PF1=2a PF1-PF2=2a(双曲线右支)(双曲线左支)PP 平面内到两个定点F1,F2的距离的差的绝对值
等于常数 2a(小于F1F2的正数)的点的轨迹叫做双曲线 双曲线定义:【解读定义】 符号表示 : |PF1-PF2|=2a 焦 点: 两个定点F1、F2 焦 距: 两焦点之间的距离 F1F2 , 2c 平面内到两个定点F1、F2的距离的差的绝对值
等于常数2a(小于F1F2的正数)的点的轨迹叫做双曲线 双曲线定义:【解读定义】 (1)若2a=2c,则轨迹是什么?思考:(2)若2a>2c,则轨迹是什么?(3)若2a=0 ,则轨迹是什么?问题3、如何求双曲线的标准方程?类比 求椭圆标准方程的基本步骤?问题4、焦点在 轴的双曲线的标准方程是什么? 焦点在x轴上, x2项的系数为正;
焦点在y轴上, y2项的系数为正.问题4、焦点在 轴的双曲线的标准方程是什么?确定焦点位置:双曲线看系数正负问题4、焦点在 轴的双曲线的标准方程是什么?确定焦点位置:椭圆看分母大小 双曲线看系数正负双曲线与椭圆之间的区别与联系a>0,b>0,但a不一定大于b, c 2=a2+b2a>b>0,a2=b2+ c 2|PF1-PF2|=2a PF1 + PF2 =2a 双曲线与椭圆之间的区别与联系|PF1-PF2|=2a PF1 + PF2 =2a 双曲线与椭圆之间的区别与联系PF1-PF2=2a PF1 + PF2 =2a ①双曲线“-”号连结,椭圆“+”号连结;例1、
【导学探疑】已知两定点 ,动点 满足 ,求动点 的轨迹方程【规范书写】解:因为 ,
由双曲线的定义可知,点 的轨迹是一条双曲线,焦点在 轴,
设所求双曲线的标准方程为
因为 所以故点 的轨迹方程为 例1、
【导学探疑】已知两定点 ,动点 满足 ,求动点 的轨迹方程变式1、去掉绝对值,求双曲线的标准方程
【规范书写】解:因为 ,
由双曲线的定义可知,点 的轨迹是一条双曲线,焦点在 轴,
设所求双曲线的标准方程为
因为 所以故点 的轨迹方程为 例1、
【导学探疑】已知两定点 ,动点 满足 ,求动点 的轨迹方程变式1、去掉绝对值,求双曲线的标准方程
变式2、 是双曲线上一点满足 ,求 的值【引学释疑】例2、求适合下列条件的双曲线的标准方程
(1) , ,焦点在 轴上(2) 经过点 ,焦点在 轴上 【引学释疑】例2、求适合下列条件的双曲线的标准方程
(1) , ,焦点在 轴上(2) 经过点 ,焦点在 轴上 变式、去掉(1)中焦点在 轴上
【引学释疑】例2、求适合下列条件的双曲线的标准方程
(1) , ,焦点在 轴上(2) 经过点 ,焦点在 轴上 变式、去掉(1)中焦点在 轴上
追踪训练:求适合下列条件的双曲线的标准方程
(1) ,
(2)一个焦点为 ,且过点 固学思疑小结反思
1、数学理论知识2、数学思想方法
双曲线 定义 标准方程类比、分类讨论Thanks for your attention!书 山 有 路 勤 为 径学 海 无 涯 苦 作 舟【课后练习】求适合下列条件的双曲线的标准方程
(1) ,
(2)与双曲线 有相同焦点,且过点
