2.2.2 间接证明课件24张PPT

课件24张PPT。间接证明直接证明：(1)综合法——(2)分析法——由因导果执果索因2000多年前，亚里士多德认为：物体自由下落时，重的比轻的快。现在我们都知道这是错的，你能从数学
的角度加以说理吗？一、【情景问题】问题1：16世纪末，伽利略用下面的思想实验反驳了
亚里士多德的结论。
假设亚里士多德的结论是正确的，
现在有两个重量不同的物体A和B，A比B重。
则A比B下落的快。
如果把A和B栓在一起（记为A+B),B会把A+B下落的
速度拖慢。因此，A+B下落的速度应比A慢。
另一方面，因为A+B比A重，按照亚里士多德的论断，
A+B的下落速度应比A快。这就产生了矛盾。
因此亚里士多德的论断是错误的。
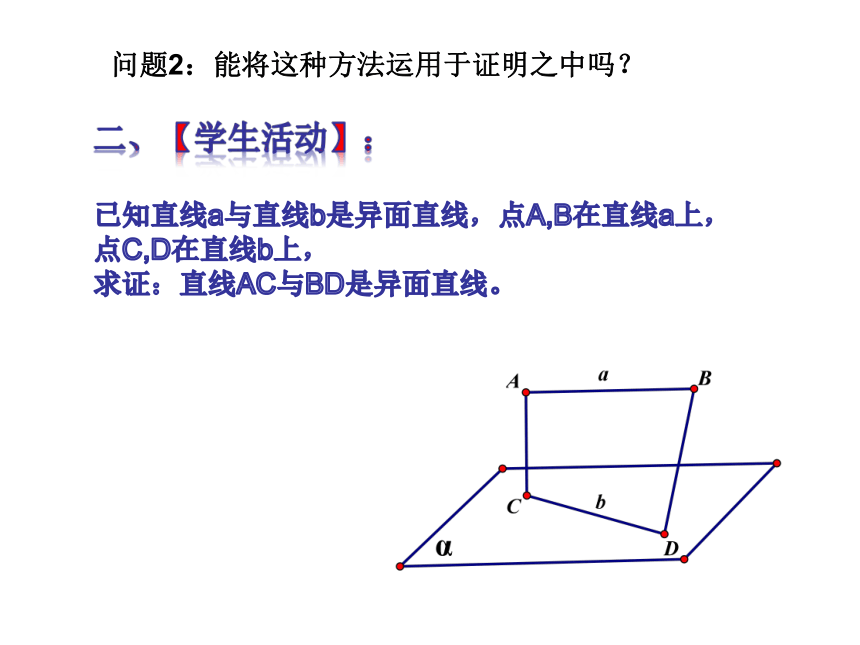
问题2：能将这种方法运用于证明之中吗？已知直线a与直线b是异面直线，点A,B在直线a上，
点C,D在直线b上，
求证：直线AC与BD是异面直线。
二、【学生活动】：三、【建构数学】：问题3：
上述证明使用的是什么证明方法？
它是怎样证明结论的？（请大家展开讨论）讨论要点：
（1）上述证明是不是直接证明？为什么？
（2）上面的证明可以分成几个步骤？
（3）分析每个步骤在证明中起了什么作用？尝试给出上述证明过程的示意图。在证明一个命题时，人们有时先假设命题不成立，从这样的假设出发，经过推理得出和已知条件矛盾，或者与定义、公理、定理等矛盾，从而得出假设命题不成立是错误的，即所求证的命题正确.这种证明方法叫做反证法（它是一种间接证明方法）。四、【数学理论】：定义：五、【数学运用】：例题4.已知0设当x0≥1时，f(x0)≥1，f(f(x0))＝x0，
求证：f(x0)＝x0.[证明]　假设f(x0)≠x0，则必有f(x0)>x0或f(x0)若f(x0)>x0≥1，由 （x≥1)
则f(x)在[1，＋∞)上为增函数，则f(f(x0))>f(x0)，
又f(f(x0))＝x0，∴x0>f(x0)，与假设矛盾，
若x0>f(x0)≥1，则f(x0)>f(f(x0))，
又f(f(x0))＝x0，∴f(x0)>x0也与假设矛盾．
综上所述，当x0≥1，f(x0)≥1且f(f(x0))＝x0时有f(x0)＝x0.课堂练习：六、【课堂小结】：1.适宜使用反证法的情况
（1）结论以否定形式出现
（2）结论以“至多-------，” ，“至少------”形式出现
（ 3） 结论的反面比原结论更具体更容易研究的命题。
2.反证法的一般步骤： （1）设结论的反面成立； (2)从这个假设出发，经过推理论证，得 出矛盾； (3)由矛盾判定假设不正确，从而肯定命题的结论正确。 归缪矛盾：
（1）与已知条件矛盾；
（2）与已有公理、定理、定义矛盾；
（3）自相矛盾。拓展训练1、平面内有四个点，没有三点共线，
证明：以任意三个点为顶点的三角形不可能
都是锐角三角形
拓展训练1、平面内有四个点，没有三点共线，求证：以任意三个点为顶点
的三角形不可能都是锐角三角形这与一个周角为360°矛盾。 拓展训练1、平面内有四个点，没有三点共线，
证明：以任意三个点为顶点的三角形不可能都是锐角三角形都是锐角三角形，即这与四边形内角和矛盾。所以，综上所述，假设不成立，从而题目结论成立。即这些三角形不可能都为锐角三角形。2.已知p3＋q3＝2，求证：p＋q≤2.[证明]　假设p＋q＞2，那么p＞2－q，
∴p3＞(2－q)3＝8－12q＋6q2－q3.
将p3＋q3＝2代入得，6q2－12q＋6＜0，
即6(q－1)2＜0.
由此得出矛盾．∴p＋q≤2.1.求证：4n+3（n为自然数）不能表示成

两个正整数的平方和。思维体操